Students can Download Tamil Nadu 11th Physics Previous Year Question Paper June 2019 Pdf in English Medium, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th Physics Previous Year Question Paper June 2019 in English Medium
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer.
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 2½ Hours
Max Marks: 70
PART – I
Answer all the questions. [15 × 1 = 15]
Question 1.
If π = 3.14, then the value of π2 is _________
(a) 9.8596
(b) 9.860
(c) 9.86
(d) 9.9
Answer:
(c) 9.86
π = 3.14
π2 = (3.14)2 = 9.8596
Rounding off, we get π2 = 9.86
Question 2.
If an object is thrown vertically upward with initial speed ‘u ’ from the ground, then the time
taken by the object to return to the ground is ________
(a) \(\frac{u^{2}}{2 g}\)
(b) \(\frac{u^{2}}{g}\)
(c) \(\frac{u}{2 g}\)
(d) \(\frac{2 u}{g}\)
Answer:
(d) \(\frac{2 u}{g}\)
When body moves upward, v = 0; s = h
v = u + at

Question 3.
If the position vector of a particle is given by \(\vec{r}=5 t^{2} \hat{i}+7 t \hat{j}+4 \hat{k}\), then its velocity lies in:
(a) X-Z plane
(b) X-Y plane
(c) along Y-direction
(d) along X- direction
Answer:
(b) X-Y plane
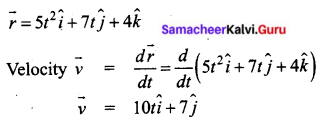
Question 4.
Force acting on a particle moving at constant speed:
(a) always zero
(b) need not be zero
(c) always non-zero
(d) cannot be concluded
Answer:
(a) always zero
![]()
Question 5.
What of the following force is pseudo force?
(a) viscous force
(b) surface tension
(c) centrifugal force
(d) cannot be concluded
Answer:
(c) centrifugal force
Question 6.
What is the minimum velocity with which a body of mass ‘m’ must enter a vertical loop of radius R, so that it can complete the loop?
(a) \(\sqrt{2 g R}\)
(b) \(\sqrt{3 g R}\)
(c) \(\sqrt{5 g R}\)
(d) \(\sqrt{g R}\)
Answer:
(c) \(\sqrt{5 g R}\)
Question 7.
A rigid body rotates with an angular momentum ‘L’. If its kinetic energy is halved, the angular momentum will be:
(a) L
(b) \(\frac{\mathrm{L}}{2}\)
(c) 2L
(d) \(\frac{\mathbf{L}}{\sqrt{2}}\)
Answer:
(d) \(\frac{\mathbf{L}}{\sqrt{2}}\)

Question 8.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The fractional force:
(a) decreases the rotational and translational motion
(b) dissipates kinetic energy as heat
(c) converts transnational energy into rotational energy
(d) decreases the rotational motion
Answer:
(c) converts transnational energy into rotational energy
![]()
Question 9.
If the radius of Earth is ‘R’, at what height acceleration due to gravity becomes zero?
(a) R
(b) \(\frac{R}{4}\)
(c) 2R
(d) \(\frac{R}{2}\)
Answer:
(d) \(\frac{R}{2}\)
Question 10.
If two wires have the same dimension but of different materials, the graph between load and extension is as follow, then which of the following is true:
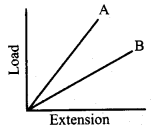
(a) YB = YA
(b) YA < YB (c) YA > YB
(d) YA = YB = 0
Answer:
(c) YA > YB
Question 11.
The wettability of a surface by a liquid depends primarily on __________
(a) viscosity
(b) surface tension
(c) density
(d) the angle of contact between the surface and the liquid
Answer:
(d) the angle of contact between the surface and the liquid
Question 12.
The efficiency of a heat engine working between 27°C and 127°C is:
(a) 50 %
(b) 25 %
(c) 12.5 %
(d) 75 %
Answer:
(b) 25 %
T1 = 127°C = 400 K
T2 = 27°C = 300 K
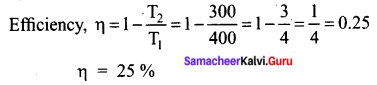
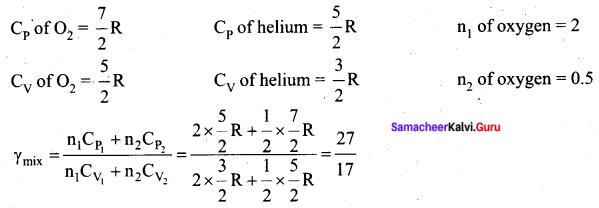
Question 13.
The ratio \(\gamma=\frac{C_{P}}{C_{V}}\) for a gas mixture consisting of 8 g of helium and 16 g of oxygen is :
(a) \(\frac{23}{15}\)
(b) \(\frac{15}{23}\)
(c) \(\frac{27}{11}\)
(d) \(\frac{17}{27}\)
Answer:
(c) \(\frac{27}{11}\)
Helium is a mono atomic gas and oxygen is diatomic gas.
Question 14.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________
(a) an ellipse
(b) a circle
(c) a parabola
(d) a straight line
Answer:
(d) a straight line
![]()
Question 15.
A person standing between two parallel hills fires a gun and hears the first echo after ‘t1’ sec, and the second echo after ‘t2’ sec. The distance between the hills is _______
(a) \(\frac{v\left(t_{1}-t_{2}\right)}{2}\)
(b) \(\frac{v\left(t_{1} t_{2}\right)}{2\left(t_{1}+t_{2}\right)}\)
(c) \(v\left(t_{1}+t_{2}\right)\)
(d) \(\frac{v}{2}\left(t_{1}+t_{2}\right)\)
Answer:
(d) \(\frac{v}{2}\left(t_{1}+t_{2}\right)\)
Distance b/w man and hill 1, d1 = \(\frac{v t_{1}}{2}\)
Distance b/w man and hill 2, d2 = \(\frac{v t_{2}}{2}\)
Distance b/w the two hills, d = d1 + d2
\(\mathrm{d}=\frac{\mathrm{v}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)}{2}\)
PART – II
Answer any six questions in which Q. No. 23 is compulsory. [6 × 2 = 12]
Question 16.
Check the following equation by dimensional method: E = mc2
Answer:
Let us assume that the Energy E depends on mass m and velocity of light c.
E ∝ ma cb
E = kmacb where K a constant
Dimensions of E = [ML2T-2]
Dimensions of m = [M]
Dimensions of c = [LT-1]
Substituting the values in the above equation [ML2T-2] = K [M]a[LT-1]b
By equating the dimensions,
a = 1; b = 2; -b = -2
E = k.mc2
The value of constant k = 1
E = mc2
This is Einstein’s mass energy relation.
![]()
Question 17.
What is the difference between scalar and vector? Give examples.
Answer:
| Scalar | Vector |
| Which has only magnitude and no direction | Which has both magnitude and direction? |
| It is a one-dimensional quantity. | It is a multi-dimensional quantity. |
| It follows ordinary algebra rules. Ex. Length, mass |
It follows vector algebra rules. Ex. force, velocity |
Question 18.
State Lami’s theorem.
Answer:
If a system of three concurrent and coplanar forces is in equilibrium, then Lami’s theorem states that the magnitude of each force of the system is proportional to sine of the angle between the other two forces.
\(\left|\overrightarrow{\mathrm{F}}_{1}\right| \propto \sin \alpha,\left|\overrightarrow{\mathrm{F}}_{2}\right| \propto \sin \beta,\left|\overrightarrow{\mathrm{F}}_{3}\right| \alpha \sin \gamma\)
Question 19.
Define the centre of gravity.
Answer:
The centre of gravity of a body is the point at which the entire weight of the body acts, irrespective of the position and orientation of the body.
Question 20.
An electron moving with velocity 2.2 × 106 m/s, revolving in a circular orbit of radius 0.53 Å. Calculate its angular velocity.
Answer:
v = 2.2 × 106 m/s
r = 0.53 Å = 0.53 × 10-10 m
Angular velocity, \(\omega=\frac{v}{r}=\frac{2.2 \times 10^{6}}{0.53 \times 10^{-10}}\)
ω = 4.15 × 1016 rads-1
Question 21.
What is Reynold’s number? Give its significance.
Answer:
It is a dimensionless number which determines the nature of the flow of fluid through a pipe. Reynold’s number is given by,
\(\mathrm{R}_{\mathrm{c}}=\frac{\rho v \mathrm{D}}{\mathrm{n}}\)
If, Rc < 1000 – streamline
Rc > 2000 – turbulent
1000 < Rc < 2000 – unsteady
Question 22.
Define specific heat capacity.
Answer:
Specific heat capacity of a substance is defined as the amount of heat energy required to raise the temperature of 1 kg of a substance by 1 Kelvin or 1°C
∆Q = ms∆T
Therefore, \(s=\frac{1}{m}\left(\frac{\Delta Q}{\Delta T}\right)\)
The SI unit for specific heat capacity is J kg-1 K-1
Question 23.
Define the root mean square speed.
Answer:
Root mean square speed is defined as the square root of the mean of the square of speeds of all molecules.
![]()
Question 24.
A particle executing SHM covers a displacement of half of the amplitude in one second. Calculate its time period.
Answer:
Displacement, X = A sin(ωt)

PART – III
Answer any six questions in which Q. No. 29 is compulsory. [6 × 3 = 18]
Question 25.
What are the limitations of dimensional analysis?
Answer:
Limitations of Dimensional analysis
- This method gives no information about the dimensionless constants in the formula like 1, 2, ……… π, e, etc.
- This method is not suitable to derive relations involving trigonometric, exponential and logarithmic functions.
- It can only check on whether a physical relation is dimensionally correct but not the correctness of the relation. For example, using dimensional analysis, \(s=u t+\frac{1}{3} a t^{2}\) is dimensionally correct whereas the correct relation is \(s=u t+\frac{1}{2} a t^{2}\)
Question 26.
Find the maximum speed at which a car turn round a curve of 36 m radius on a level road. Given the co-eff. of friction between the tyre and road is 0.53.
Answer:
Radius of the curve r = 36 m
Coefficient of friction µ = 0.53
Acceleration due to. gravity g = 10 ms-2
\(v_{\max }=\sqrt{\mu r g}=\sqrt{0.53 \times 36 \times 10}=13.81 \mathrm{ms}^{-1}\)
Question 27.
Give the difference between elastic and inelastic collision.
Answer:
| Elastic collision | Inelastic collision |
| 1. Total kinetic energy is conserved. | 1. Total kinetic energy is not conserved. |
| 2. Forces involved are conservative forces. | 2. Forces involved are non-conservative forces. |
| 3. Mechanical energy is not dissipated. | 3. Mechanical energy is dissipated into heat, light and sound etc. |
Question 28.
The position vector of the particle has a length of 1 m makes an angle of 30° with X-axis. What are the lengths of x and y components of the position vector?
Answer:
Given:
Length of position vector = 1 m
Angle made with x-axis = 30
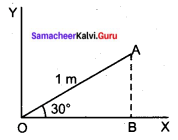
Length of X component (OB) = OA cos θ = 1 × cos 30°
\(l_{x}=\frac{\sqrt{3}}{2} \mathrm{m}\) (or) 0.87 m
Length of Y component (AB) = OA sin θ = 1 × sin 30° = \(\frac{1}{2}\) = 0.5 m.
ly = 0.5 m
![]()
Question 29.
State Kepler’s laws.
Answer:
- Law of Orbits: Each planet revolves moves around the Sun in an elliptical orbit with the Sun at one of the foci of the ellipse.
- Law of the area: The radial vector line joining the Sun to a planet sweeps equal areas in equal intervals of time.
- Law of the period: The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse.
T2 ∝ a3
\(\frac{T^{2}}{a^{3}}\) = constant
Question 30.
Explain any three factors affecting the surface tension of a liquid.
Answer:
- The presence of any contamination or impurities considerably affects the force of surface tension depending upon the degree of contamination.
- The presence of dissolved substances can also affect the value of surface tension. For example, a highly soluble substance like sodium chloride (NaCl) when dissolved in water (H2O) increases the surface tension of water. But the sparingly soluble substance like phenol or soap solution when mixed in water decreases the surface tension of water.
- Electrification effects surface tension. When a liquid is electrified, surface tension decreases. Since external force acts on the liquid surface due to electrification, the area of the liquid surface increases which acts against the contraction phenomenon of the system.
Question 31.
Define degrees of freedom. Give an example.
Answer:
The minimum number of independent coordinates needed to specify the position and configuration of a thermo-dynamical system in space is called the degree of freedom of the So its degree of freedom is one.
Example:
- A free particle moving along x-axis needs only one coordinate to specify it completely. So its degree of freedom is one.
- Similarly, a particle moving over a plane has two degrees of freedom.
- A particle moving in space has three degrees of freedom.
![]()
Question 32.
Explain any three applications of reflection of a sound wave.
Answer:
(a) Stethoscope: It works on the principle of multiple reflections. It consists of three main parts:
- Chest piece
- Earpiece
- Rubber tube
(b) Echo: An echo is a repetition of sound produced by the reflection of sound waves from a wall, mountain or other obstructing surfaces. The speed of sound in air at 20°C is 344 ms-1. If we shout at a wall which is at 344 m away, then the sound will take 1 second to reach the wall. After reflection, the sound will take one more second to reach us. Therefore, we hear the echo after two seconds.
(c) SONAR: Sound Navigation and Ranging. Sonar systems make use of reflections of sound waves in the water to locate the position or motion of an object. Similarly, dolphins and bats use the sonar principle to find their way in the darkness.
Question 33.
A child is playing on a sliding board. If he is sliding down:
(a) Mention the forces acting on the child.
(b) Draw FBD (Free Body Diagram).
(c) Write the force equation.
Answer:
(a) ma = mg sin θ – fk
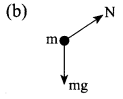
(c) F = mg sin θ
PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34.
(a) Explain in detail the triangle law of addition.
Answer:
Let us consider two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) as shown in figure. To find the resultant of the two vectors we apply the triangular law of addition as follows:
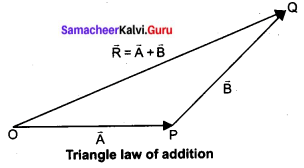
Represent the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure. To explain further, the head of the first vector \(\overrightarrow{\mathrm{A}}\) is connected to the tail of the second vector \(\overrightarrow{\mathrm{A}}\). Let θ be the angle between \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\). Then \(\overrightarrow{\mathrm{R}}\) is the resultant vector connecting the tail of the first vector \(\overrightarrow{\mathrm{A}}\) to the head of the second vector \(\overrightarrow{\mathrm{B}}\). The magnitude of \(\overrightarrow{\mathrm{R}}\)(resultant) is given geometrically by the length of \(\overrightarrow{\mathrm{R}}\) (OQ) and the direction of the resultant vector is the angle between \(\overrightarrow{\mathrm{R}}\) and \(\overrightarrow{\mathrm{A}}\). Thus we write \(\overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)
\(\overrightarrow{\mathrm{OQ}}=\overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{PQ}}\)
1. Magnitude of resultant vector: The magnitude and angle of the resultant vector are determined by using triangle law of vectors as follows.
From the figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right-angled triangle.
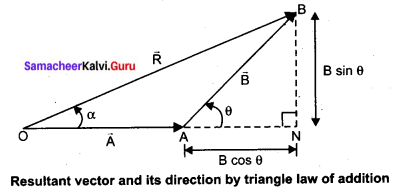


[OR]
Question 34(b).
Discuss the four types of oscillation.
Answer:
(i) Free oscillations: When the oscillator is allowed to oscillate by displacing its position from the equilibrium position, it oscillates with a frequency which is equal to the natural frequency of the oscillator. Such an oscillation or vibration is known as free oscillation or free vibration. In this case, the amplitude, frequency and the energy of the vibrating object remain constant.
Examples:
- The vibration of a tuning fork.
- Vibration in a stretched string.
- Oscillation of a simple pendulum.
- Oscillations of a spring-mass system.
(ii) Damped oscillations: During the oscillation of a simple pendulum (in the previous case), we have assumed that the amplitude of the oscillation is constant and also the total energy of the oscillator is constant. But in reality, in a medium, due to the presence of friction and air drag, the amplitude of oscillation decreases as time progresses. It implies that the oscillation is not sustained and the energy of the SHM decreases gradually indicating the loss of energy. The energy lost is absorbed by the surrounding medium. This type of oscillatory motion is known as damped oscillation. In other words, if an oscillator moves in a resistive medium, its amplitude goes on decreasing and the energy of the oscillator is used to do work against the resistive medium. The motion of the oscillator is said to be damped and in this case, the resistive force (or damping force) is proportional to the velocity of the oscillator.
Examples:
- The oscillations of a pendulum (including air friction) or pendulum oscillating inside an oil-filled container.
- Electromagnetic oscillations in a tank circuit.
- Oscillations in a dead beat and ballistic galvanometers.
(iii) Maintained oscillations: While playing in swing, the oscillations will stop after a few cycles, this is due to damping. To avoid damping we have to supply a push to sustain oscillations. By supplying energy from an external source, the amplitude of the oscillation can be made constant. Such vibrations are known as maintained vibrations.
Example:
The vibration of a tuning fork getting energy from a battery or from the external power supply.
(iv) Forced oscillations: Any oscillator driven by an external periodic agency to overcome the damping is known as a forced oscillator or driven oscillator. In this type of vibration, the body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force. Such vibrations are known as forced vibrations.
Example: Soundboards of stringed instruments.
![]()
Question 35.
(a) Explain the vertical motion of blocks connected by a string.
Answer:
Vertical motion: Consider two blocks of masses m1 and m2 (m1 > m2) connected by light and inextensible string that passes over a pulley as shown in Figure.
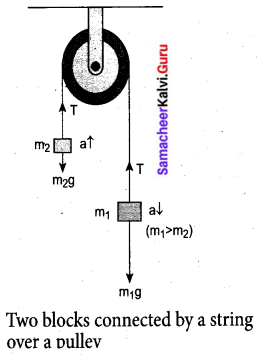
Let the tension in the string be T and acceleration a.
When the system is released, both the blocks start moving, m2 vertically upward and m1 downward with same acceleration a. The gravitational force m1g on mass m1 is used in lifting the mass m2.
The upward direction is chosen as y-direction. The free-body diagrams of both masses are shown in Figure.
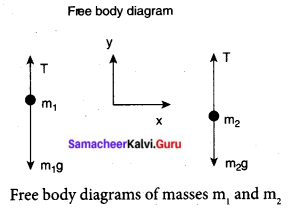
Applying Newton’s second law for mass m2
\(\mathrm{T} \hat{j}-m_{2} g \hat{j}=m_{2} a \hat{j}\)
The left-hand side of the above equation is the total force that acts on m2 and the right-hand side is the product of mass and acceleration of m2 in the y-direction.
By comparing the components on both sides, we get
T – m2g = m2a …… (1)
Similarly, applying Newton’s second law for mass m1
\(\mathbf{T} \hat{j}-m_{1} g \hat{j}=-m_{1} a \hat{j}\)
As mass mx moves downward (\(-\hat{j}\)), its acceleration is along (\(-\hat{j}\)) By comparing the components on both sides, we get
T – m1g = -m1a
m1g – T = m1a ……. (2)
Adding equations (1) and (2), we get
m1g – m2g = m1a + m2a
(m1 – m2)g = (m1 + m2)a …….. (3)
From equation (3), the acceleration of both the masses is
\(a=\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g\) …… (4)
If both the masses are equal (m1 = m2), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).

[OR]
Question 35(b).
What are stationary waves? Write the characteristics of stationary waves.
Answer:
Explanation of stationary waves: When the wave hits the rigid boundary it bounces back to the original medium and can interfere with the original waves. A pattern is formed, which are known as standing waves or stationary waves.
Characteristics of stationary waves:
- Stationary waves are characterised by the confinement of a wave disturbance between two rigid boundaries. This means, the wave does not move forward or backwards in a medium (does not advance), it remains steady at its place. Therefore, they are called “stationary waves or standing waves”.
- Certain points in the region in which the wave exists have maximum amplitude, called as anti-nodes and at certain points, the amplitude is minimum or zero, called as nodes.
- The distance between two consecutive nodes (or) anti-nodes is \(\frac{\lambda}{2}\)
- The distance between a node and its neighbouring anti-node is \(\frac{\lambda}{4}\)
- The transfer of energy along the standing wave is zero.
![]()
Question 36(a).
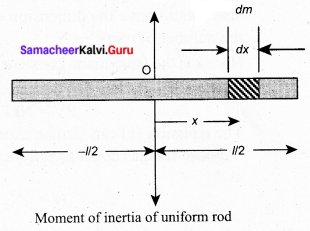
Derive the expression of a moment of inertia of the rod about an axis passing through its centre and perpendicular to the rod.
Answer:
Let us consider a uniform rod of mass (M) and length (l) as shown in the figure. Let us find an expression for moment of inertia of this rod about an axis that passes through the centre of mass and perpendicular to the rod. First, an origin is to be fixed for the coordinate system so that it coincides with the centre of mass, which is also the geometric centre of the rod. The rod is now along the x-axis. We take an infinitesimally small mass (dm) at a distance (x) from the origin. The moment of inertia (dl) of this mass (dm) about the axis is, dl = (dm)x2
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, \(\lambda=\frac{\mathbf{M}}{l}\)
The (dm) mass of the infinitesimally small length as, dm = λdx = \(\frac{M}{l}\) dx
The moment of inertia (i) of the entire rod can be found by integrating dI,
\(\begin{aligned}
&\mathrm{I}=\int d \mathrm{I}=\int(d m) x^{2}=\int\left(\frac{\mathrm{M}}{l} d x\right) x^{2}\\
&\mathrm{I}=\frac{\mathrm{M}}{l} \int x^{2} d x
\end{aligned}\)
As the mass is distributed on either side of the origin, the limits for integration are taken from to -l/2 to l/2

[OR]
Question 36(b).
State ideal gas laws. Derive the equation of state for an ideal gas.
Answer:
Boyle’s law: For a given gas at low pressure (density) kept in a container of volume V, experiments revealed the following information.
When the gas is kept at a constant temperature, the pressure of the gas is inversely proportional to the volume P ∝ \(\frac{1}{V}\)
Charles’ law: When the gas is kept at constant pressure, the volume of the gas is directly proportional to absolute temperature V ∝ T.
By combining these two equations we have
PV = CT. Here C is a positive constant.
We can infer that C is proportional to the number of particles in the gas container by considering the following argument. If we take two containers of the same type of gas with the same volume V, same pressure P and same temperature T, then the gas in each container obeys the above equation. PV = CT. If the two containers of gas are considered as a single system, then the pressure and temperature of this combined system will be same but volume will be twice and a number of particles will also be double.
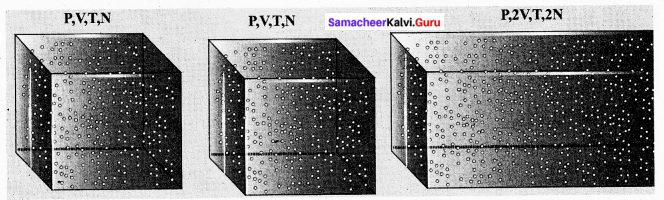
For this combined system, V becomes 2V, so C should also double to match with the ideal gas equation \(\frac{P(2 V)}{T}=2 C\). It implies that C must depend on the number of particles in the gas and also should have the dimension of \(\left[\frac{\mathrm{PV}}{\mathrm{T}}\right]=\mathrm{JK}^{-1}\). So we can write the constant C as k times the number of particles N.
Here k is the Boltzmann constant (1.381 × 10-23 JK-1) and it is found to be a universal constant. So the ideal gas law can be stated as follows
PV = NkT ……..(1)
The equation (1) can also be expressed in terms of mole.
Suppose if the gas contains µ mole of particles then the total number of particles can be written as N = µNA …(2)
where NA is Avogadro number (6.023 × 1023 mol-1)
Substituting for N from equation (2), the equation (1) becomes PV = µNAkT. Here NAk = R called universal gas constant and its value is 8.314 J /mol. K
So the ideal gas law can be written for µ mole of gas as
PV = µRT ……..(3)
This is called the equation of state for an ideal gas. It relates the pressure, volume and temperature of the thermodynamic system at equilibrium.
Question 37(a).
Derive the expression of escape speed.
Answer:
Consider an object of mass M on the surface of the Earth. When it is thrown up with an initial speed vi, the initial total energy of the object is
\(\mathrm{E}_{i}=\frac{1}{2} \mathrm{M} v_{i}^{2}-\frac{\mathrm{GMM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}}\) ……. (1)
where ME is the mass of the Earth and RE the radius of the Earth. The term \(-\frac{\mathrm{GMM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}}\) is the potential energy of the mass M.
When the object reaches a height far away from Earth and hence treated as approaching infinity, the gravitational potential energy becomes zero [U(∞) = 0] and the kinetic energy becomes zero as well. Therefore the final total energy of the object becomes zero. This is for minimum energy and for minimum speed to escape. Otherwise, kinetic energy can be nonzero.
Ef = 0
According to the law of energy conservation,
Ei = Ef ……. (2)
Substituting (1) in (2) we get,
\(\frac{1}{2} \mathrm{M} v_{i}^{2}-\frac{\mathrm{GMM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}}=0\)
\(\frac{1}{2} \mathrm{M} v_{i}^{2}=\frac{\mathrm{GMM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}}\) …….(3)
Consider the escape speed, the minimum speed required by an object to escape Earth’s gravitational field, hence replace vi with ve i.e.,
\(\frac{1}{2} M v_{e}^{2}=\frac{G M M_{E}}{R_{E}}\)
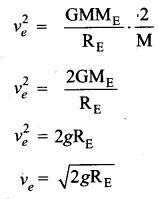
From equation (4) the escape speed depends on two factors acceleration due to gravity and radius of the Earth. It is completely independent of the mass of the object. By substituting the values of g (9.8 ms-2) and R, = 6400 km, the escape speed of the Earth is vg = 11.2 kms-1. The escape speed is independent of the direction in which the object is thrown. Irrespective of whether the object is thrown vertically up, radially outwards or tangentially it requires the same initial speed to escape Earth’s gravity.
[OR]
Question 37(b).
Explain the different types of moduli of elasticity.
Answer:
From Hooke’s law, the stress in a body is proportional to the corresponding strain, provided the deformation is very small. Here we shall define the elastic modulus of a given material. There are three types of elastic modulus.
(a) Young’s modulus (b) Rigidity modulus (or Shear modulus) (c) Bulk modulus
Young’s Modulus: When a wire is stretched or compressed, then the ratio between tensile stress (or compressive stress) and tensile strain (or compressive strain) is defined as Young’s modules.

The negative sign indicates when pressure is applied on the body, its volume decreases. Further, the equation implies that a material can be easily compressed if it has a small value of bulk modulus. In other words, bulk modulus measures the resistance of solids to change in their volume. For example, we know that gases can be easily compressed than solids, which means, gas has a small value of bulk modulus compared to solids. The S.I. unit of K is the same as that of pressure i.e., Nm-2 or Pa (pascal).
The rigidity modulus or shear modulus: The rigidity modulus is defined as the ratio of the shearing stress to shearing strain,

Further, the above implies, that a material can be easily twisted if it has a small value of rigidity modulus. For example, consider a wire, when it is twisted through an angle 0, a restoring torque is developed, that is
τ ∝ θ
This means that for a larger torque, the wire will twist by a larger amount (angle of shear θ is large). Since rigidity modulus is inversely proportional to the angle of shear, the modulus of rigidity is small. The S.I. unit of ηR is the same as that of pressure i.e., Nm-2 or pascal.
![]()
Question 38.
(a) Two objects of masses 3 kg and 6 kg are moving with the same momentum of 30 kgms-1.
(i) Will they have the same kinetic energy?
(ii) Will they have the same speed? Prove it.
Answer:
m1 = 3 kg and m2 = 6 kg
P = 30 kg ms-1

[OR]
Question 38(b).
In a series of successive measurements in an experiment, the readings of a period of rotation of a wheel were found out to be 2.15s, 2.25s, 2.28s and 2.32s. Calculate:
(i) mean value of the period of rotation
(ii) absolute error in each measurement
(iii) mean absolute error
(iv) relative error and
(v) percentage error. Express the result in proper form.
Answer:

