Students can Download Samacheer Kalvi 10th Maths Model Question Paper 1 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Model Question Paper 1 English Medium
Instructions
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
- Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
- Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 100
PART – I
I. Choose the correct answer. Answer all the questions. [14 × 1 = 14]
Question 1.
If {(a, 8),(6, b)} represents an identity function, then the value of a and b are respectively ……………. .
(1) (8,6)
(2) (8,8)
(3) (6,8)
(4) (6,6) .
Answer:
(1) (8,6)
![]()
Question 2.
If the H.C.F of 65 and 117 is expressible in the form of 65m -117, then the value of m is ……………. .
(1) 4
(2) 2
(3) 1
(4) 3
Answer:
(2) 2
Question 3.
The next term ol the sequence \(\frac{3}{16}, \frac{1}{8}, \frac{1}{12}, \frac{1}{18}\) is …………… .
(1) \(\frac{1}{24}\)
(2) \(\frac{1}{27}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{1}{81}\)
Answer:
(2) \(\frac{1}{27}\)
Question 4.
Which of the following should be added to make x4 + 64 a perfect square ……………… .
(1) 4x2
(2) 16x2
(3) 8x2
(4) -8x2
Answer:
(2) 16x2
Question 5.
Find the matrix x if 2x + \(\left[ \begin{matrix} 1 & 3 \\ 5 & 7 \end{matrix} \right] =\left[ \begin{matrix} 5 & 7 \\ 9 & 5 \end{matrix} \right] \) ……………. .
(1) \(\left[ \begin{matrix} -2 & -2 \\ 2 & -1 \end{matrix} \right] \)
(2) \(\left[ \begin{matrix} 2 & 2 \\ 2 & -1 \end{matrix} \right] \)
(3) \(\left[ \begin{matrix} 1 & 2 \\ 2 & 2 \end{matrix} \right] \)
(4) \(\left[ \begin{matrix} 2 & 1 \\ 2 & 2 \end{matrix} \right] \)
Answer:
(2) \(\left[ \begin{matrix} 2 & 2 \\ 2 & -1 \end{matrix} \right] \)
Question 6.
Two poles of heights 6 m and 11 m stand vertically on a plane ground if the distance between their feet is 12m, what is the distance between their tops?
(1) 13 m
(2) 14 m
(3) 15 m
(4) 12.8 m
Answer:
(1) 13 m
Question 7.
If (5, 7), (3,p) and (6, 6) are collinear then the value of p is ……………… .
(1) 3
(2) 6
(3) 9
(4) 12
Answer:
(3) 9
Question 8.
The value of sin2θ + \(\frac{1}{1+\tan ^{2} \theta}\) is equal to …………….. .
(1) tan2θ
(2) 1
(3) cot2θ
(4) 0
Answer:
(2) 1
Question 9.
If the radius of the base of a cone is tripled and the height is doubled then the volume is ……………… .
(1) made 6 times
(2) made 18 times
(3) made 12 times
(4) unchanged
Answer:
(2) made 18 times
![]()
Question 10.
Standard deviation of a collection of data is 2√2. If each value is multiplied by 3, then the standard deviation of the new data is
……………… .
(1) √l2
(2) 4√2
(3) 6√2
(4) 9√2
Answer:
(3) 6√2
Question 11.
A page is selected at random from a book. The probability that the digit at unit place of the page number chosen’ is less than 7 is …………. .
(1) \(\frac{3}{10}\)
(2) \(\frac{7}{10}\)
(3) \(\frac{3}{9}\)
(4) \(\frac{7}{9}\)
Answer:
(2) \(\frac{7}{10}\)
Question 12.
If f = {(6, 3), (8, 9), (5, 3), (-1, 6)} then the pre-images of 3 are ……………… .
(1) 5 and -1
(2) 6 and 8
(3) 8 and -1
(4) 6 and 5
Answer:
(4) 6 and 5
Question 13.
If a and p are the zeros 6f the polynomial P(x) = 4x2 + 3x + 7 then \(\frac{1}{\alpha}+\frac{1}{\beta}\) is equal to …………….. .
(1) \(\frac{7}{3}\)
(2) \(\frac{-7}{3}\)
(3) \(\frac{3}{7}\)
(4) \(\frac{-3}{7}\)
Answer:
(4) \(\frac{-3}{7}\)
Question 14.
The probability that a-leap year will have 53 Fridays or 53 Saturdays is …………….. .
(1) \(\frac{2}{7}\)
(2) \(\frac{1}{7}\)
(3) \(\frac{4}{7}\)
(4) \(\frac{3}{7}\)
Answer:
(4) \(\frac{3}{7}\)
PART – II
II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]
Question 15.
A relation “f” is defined by f(x) = x2 – 2 where x ∈ {-2, -1, 0, 3}
(i) List the elements of f
(ii) If f a function?
Answer:
f(x) = x2 – 2 where x ∈ {-2,-1, 0, 3}
(i) f(-2) = (-2)2 – 2 = 2 ; f(-1) = (-1)2 – 2 = -1
f(0) = (0)2 – 2 = -2 ; f(3) = (3)2 – 2 = 7
Therefore, f = {(-2,2), (-1,-1), (0,-2), (3,7)}
(ii) We note that each element in the domain of f has a unique image.
Therefore f is a function.
![]()
Question 16.
Let f(x) = x2 – 1. Find fofof
Answer:
fofof = fof [(x)]
= fof (x2 – 1)
= f (x2 – 1)2 – 1
= f (x4 – 2x2 + 1 – 1)
= f (x4 – 2x2)
fofof = (x4 – 2x2)2 – 1
Question 17.
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Answer:
Find the L.C.M of 35, 56, and 91
35 = 5 × 7
56 = 2 × 2 × 2 × 7
91 = 7 × 13
L.C.M = 23 × 5 × 7 × 13
= 3640
Since it leaves remainder 7
The required number = 3640 + 7 = 3647
∴ The smallest number is 3647
Question 18.
In a G.P. 729, 243, 81,… find t7.
Answer:
The G.P. is 729,243,81, …………..
a = 729; r = \(\frac{t_{2}}{t_{1}}=\frac{243}{729}=\frac{81}{243}=\frac{27}{81}=\frac{3}{9}=\frac{1}{3}\)
tn = a rn – 1
t7 = 729 \(\left(\frac{1}{3}\right)^{7-1}\)
= \(729\left(\frac{1}{3}\right)^{6}=729 \times \frac{1}{729}=1\)
∴ The 7th term is 1
Question 19.
Find the excluded values of the expression \(\frac{t}{t^{2}-5 t+6}\)
Answer:
The expression \(\frac{t}{t^{2}-5 t+6}\) is undefined
when t2 – 5t + 6 = 0
(t – 3) (t – 2) = 0
t – 3 = 0 or t – 2 = 0
t = 3 or t = 2
The excluded values are 2 and 3
Question 20.
Find the square root of 9x2 – 24xy + 30xz – 40yz + 25z2 + 16y2
Answer:
\(\sqrt{9 x^{2}-24 x y+30 x z-40 y z+25 z^{2}+16 y^{2}}\)
\(\sqrt{(3 x)^{2}+(4 y)^{2}+(5 z)^{2}-2(3 x)(4 y)-2(4 y)(5 z)+2(3 x)(5 z)}\)
\(\sqrt{(3 x-4 y+5 z)^{2}}\) [using (a – b + c)2 = a2 + b2 + c2 -2ab -2bc + 2ac]
= |3x – 4y + 5z|
Question 21.
construct a 3 x 3 matrix whose elements are given by aij = \(\frac{(i+j)^{3}}{3}\)
Answer:
aij = \(\frac{(i+j)^{3}}{3}\)

![]()
Question 22.
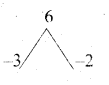
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
Answer:
Given ∆ABC ~ ∆DEF
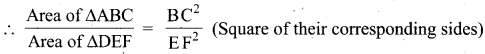
\(\frac{9}{16}=\frac{(2.1)^{2}}{\mathrm{EF}^{2}}\)
\(\left(\frac{3}{4}\right)^{2}=\left(\frac{2.1}{\mathrm{EF}}\right)^{2}\)
\(\frac{3}{4}=\frac{2.1}{\mathrm{EF}}\)
EF = \(\frac{4 \times 2.1}{3}\) = 2.8 cm
Length of EF = 2.8 cm
Question 23.
If the area of the triangle formed by the vertices (p,p), (5,6), (5, -2) is 32 sq.units. Find the value of ‘p’.
Answer:
Let the vertices be A (p,p), B (5, 6) and C (5, -2)
Area of a triangle = 32 sq. units
\(\frac{1}{2}\)[x1y2 + x2y3 + x3y1) – (x2y1 + x3y2 + x1y3] = 32
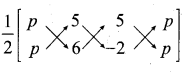
\(\frac{1}{2}\)[(6p – 10 + 5p) – (5p + 30 – 2p)] = 32
\(\frac{1}{2}\)[11p – 10 – 3p – 30] = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40 ⇒ 8p = 104
p = \(\frac{104}{8}\) = 13
The value of p = 13
Question 24.
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height 10 √3 m.
Answer:
Height of the tower (AC) = 10 √3 m
Distance between the base of the tower and point of observation (AB) = 30 m
Let the angle of elevation ∠ABC be θ
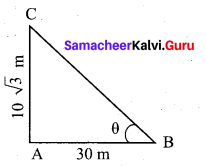
In the right ∆ ABC, tan θ = \(\frac{A C}{A B}\)
\(=\frac{10 \sqrt{3}}{30}=\frac{\sqrt{3}}{3}\)
tan θ = \(\frac{1}{\sqrt{3}}\) = tan 30°
∴ Angle of inclination is 30°
Question 25.
Find the diameter of a sphere whose surface area is 154m2.
Answer:
Let r be the radius of the sphere.
Given that, surface area of sphere = 154 m2
4πr2 = 154
4 × \(\frac{22}{7}\) × r2 = 154
gives r2 = \(154 \times \frac{1}{4} \times \frac{7}{22}\)
hence, r2 = \(\frac{49}{4}\) we get r = \(\frac{7}{2}\)
Therefore, diameter is 7m
![]()
Question 26.
Find the standard deviation and the variance of first 23 natural numbers.
Answer:
Standard deviation of first “n” natural numbers = \(\sqrt{\frac{n^{2}-1}{12}}\)
Standard deviation of first 23 natural numbers = \(\sqrt{\frac{23^{2}-1}{12}}\)
= \(\sqrt{\frac{529 – 1}{12}}\)
\(=\sqrt{\frac{528}{12}}\)
= √44 (variance)
Variance = 44 and standard deviation = 6.63
Question 27.
Form the quadratic equation whose roots are 3 + √7 ; 3 – √7
Answer:
Sum of the roots = 3 + √7 + 3 – √7
= 6
Product of the roots = (3 + √7)(3 – √7)
= 9 – 7 = 2 .
The required equation is
x2 – (sum of the roots) x + product of the roots = 0
x2 – (6) x + 2 = 0
x2 – 6x + 2 = 0
Question 28.
Two coins are tossed together. What is the probability of getting at most one head?
Answer:
Sample space = {HH, HT, TH, TT}
n(S) = 4
Let A be the event of getting atmost one head A = {HT, TH, TT}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{4}\)
The probability is \(\frac{3}{4}\)
![]()
PART – III
III. Answer any ten questions. Question No 42 is compulsory. [10 × 5 = 50]
Question 29.

Answer:
f(x) = 6x + 1 ; x = {-5, -4, -3, -2, -1, 0, 1}
f(x) = 5x2 – 1 ; x = {2,3,4,5}
f(x) = 3x – 4; x = {6,7,8,9}
(i) f(-3) + f(2)
f(x) = 6x+1
f(3) = 6(-3) + 1 = -18 + 1 = -17
f(x) = 5x2 – 1
f(2) = 5(2)2 – 1 = 20 – 1 = 19
f(-3) + f(2) = -17 + 19 = 2
(ii) f(7) – f(1)
f(x) = 3x – 4
f(7) = 3(7) – 4= 21 – 4 = 17
f(x) = 6x + 1
f(1) = 6(1)+ 1 = 6 + 1 = 7
f(7) – f(1) = 17 – 7
= 10
(iii) 2f(4) + f(8)
f(x) = 5x2 – 1
f(4) = 5(4)2 – 1 = 15(16) – 1
= 80 – 1 = 79
f(x) = 3x – 4
f(8) = 3(8) – 4 = 24 – 4 = 20
2f(4) + f(8) = 2(79) + 20
= 158 + 20 .
= 178
(iv) \(\frac{2 f(-2)-f(6)}{f(4)+f(-2)}\)
f(x) = 6x + 1
f(-2) = 6(-2) + 1 = -12 + 1 = -11
f(x) = 3x – 4
f(6) = 3(6) – 4 = 18 – 4 = 14
f(x) = 5x2 – 1
f(4) = 5(4)2 – 1 = 5(16) – 1
= 80 – 1 = 79
f(x) = 6x+1
f(-2) = 6(-2) + 1 = -12 + 1 = -11
\(\frac{2 f(-2)-f(6)}{f(4)+f(-2)}\) = \(\frac{2(-11)-14}{79-11}\)
= \(\frac{-22-14}{68}=\frac{-36}{68}=\frac{-9}{17}\)
![]()
Question 30.
If f(x) = 2x + 3, g(x) = 1 – 2x and h(x) = 3x Prove that fo(goh) = (fog)oh
Answer:
f(x) = 2x + 3, g(x) = 1 – 2x, h(x) = 3x
Now, (fog)(x) = f(g(x)) = f(1 – 2x) = 2(1 – 2x) + 3 = 5 – 4x
Then, (fog)oh(x) = (fog) (h(x)) = (fog)(3x) = 5 – 4(3x) = 5 – 12x ….(1)
(goh)(x) = g(h(x)) = g(3x) = 1 – 2(3x) = 1 – 6x
So, fo (goh)(x) = f(1 – 6x) = 2(1 – 6x) + 3 = 5 – 12x …….. (2)
From (1) and (2), we get (fog)oh = fo(goh)
Question 31.
If S1 , S2 , S3, ……. Smare the sums of n terms of m A.P.,s whose first terms are 1,2, 3, …….. m and whose common differences are 1,3,5,….(2m – 1) respectively, then show that (S1 + S2 + S3 + …….. + Sm) = \(\frac { 1 }{ 2 }\) mn(mn + 1)
Answer:
First terms of an A.P and 2, 3 ……….. m
The common difference are 1, 3, 5 , ………….. (2m – 1)
Sn = \(\frac { n }{ 2 }\)[2a+(n – 1)d]
S1 = \(\frac { n }{ 2 }\)[2+(n – 1)(1)]
= \(\frac { n }{ 2 }\)[2 + n – 1]
S1 = \(\frac { n }{ 2 }\)[n + 1] …….. (1)
S2 = \(\frac { n }{ 2 }\)[2(2) + (n – 1)3]
= \(\frac { n }{ 2 }\)[4 + 3n – 3]
S2 = \(\frac { n }{ 2 }\)(3n – 2) ……. (2)
S3 = \(\frac { n }{ 2 }\)[2(3) + (n – 1)5]
= \(\frac { n }{ 2 }\)[6 + 5n – 5}
= \(\frac { n }{ 2 }\)[5n + 1] …….. (3)
Sm = \(\frac { n }{ 2 }\)[2m + (n – 1)(2m – 1)]
= \(\frac { n }{ 2 }\)[2m + 2mn – n – m – 2m + 1]
= \(\frac { n }{ 2 }\)[n(2m – 1) + 1]
By adding (1) (2) (3) we get
S1 + S2 + S3 + ……….. + Sm = \(\frac { n }{ 2 }\)(n + 1) + \(\frac { n }{ 2 }\)(3n + 1) + \(\frac { n }{ 2 }\)(5n + 1)+ …………+ \(\frac { n }{ 2 }\)[n(2m – 1) + 1]
= \(\frac { n }{ 2 }\)[n + 1 + 3n + 1 + 5n + 1 …………… + n(2m – 1) + m]
= \(\frac { n }{ 2 }\)[n + 3n + 5n + ………….. + n(2m – 1) + m]
= \(\frac { n }{ 2 }\)[n\((\frac { m }{ 2 })\)(2m) + m]
= \(\frac { n }{ 2 }\)[nm2 + m]
S1 + S2 + S3 + ……… + Sm = \(\frac { mn }{ 2 }\)[nm + 1]
Hint:
1 + 3 + 5 + …….. + 2m – 1
Sn = \(\frac { n }{ 2 }\)(a + 1)
= \(\frac { m }{ 2 }\) (1 + 2m – 1)
= \(\frac { m }{ 2 }\) (2m)
![]()
Question 32.
Find the sum to n terms of the series 0.4 + 0.44 + 0.444 + ………. to n terms
Answer:
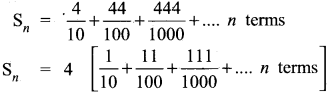

Question 33.
Vani, her father and her grand father have an average age of 53. One-half of her grand father’s age plus one-third of her father’s age plus one fourth of Vani’s age is 65. If 4 years ago Vani’s grandfather was four times as old as Vani then how old are they all now?
Answer:
Let the age of Vani be”x” years
Vani father age = “y” years
Vani grand father = “z” years .
By the given first condition.
\(\frac{x+y+z}{3}=53\)
x + y + z = 159 ….(1)
By the given 2nd condition.
\(\frac{1}{2} z+\frac{1}{3} y+\frac{1}{4} x=65\)
Multiply by 12
6z + 4y + 3x = 780 .
3x + 4y + 6z = 780 ….(2)
By the given 3rd condition
z – 4 = 4 (x – 4) ⇒ z – 4 = 4x – 16
– 4x + z = – 16 + 4
4x – z = 12 ….(3)

Substitute the value of x = 24 in (3)
4 (24) – z = 12
96 – z = 12
– z = 12 – 96
z = 84
Substitute the value of x = 24 and
z = 84 in (1)
24 + y + 84 = 159
y + 108 = 159
y = 159 – 108
= 51
Vani age = 24 years
Vani’s father age = 51 years
Vani grand father age = 84 years
![]()
Question 34.
Find the values of a and b if the following polynomials are perfect squares. ax4 + bx3 + 361x2 + 220.x + 100
Answer:
Re-arrange the order we get .
100 + 220x + 361x2 + by3 + ax4

Since it is a perfect square
b – 264 = 0
b = 264
a – 144 = 0
a = 144
∴ The value of a = 144 and b = 264
Question 35.
State and prove Pythagoras Theorem
Answer:
Statement
In a right angle triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
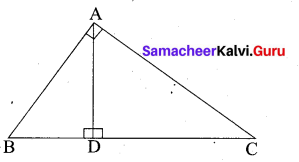
Proof
Given : In ∆ABC, ∠A = 90°.
To prove : AB2 + AC2 = BC2
Construction : Draw AD ⊥ BC
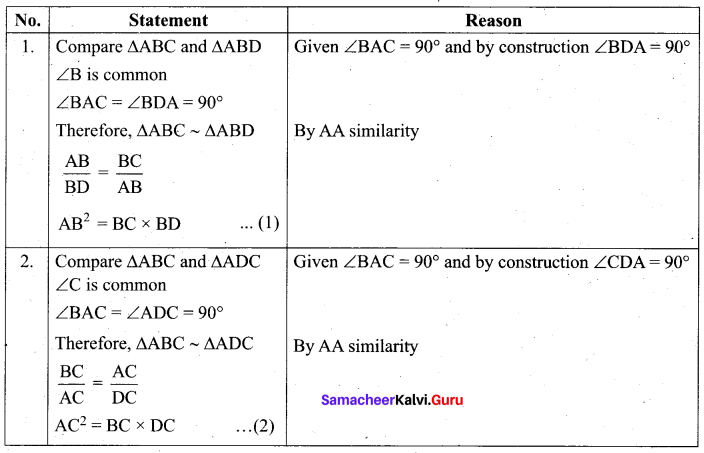
Adding (1) and (2) we get
AB2 + AC2 = BC × BD + BC × DC
= BC (BD + DC) = BC × BC
AB2 + AC2 = BC2
Hence the theorem is proved.
![]()
Question 36.
Find the equation of the median and altitude of AABC through A where the vertices are A(6, 2), B(-5, -1) and C(1,9).
Answer:
(i) To find median
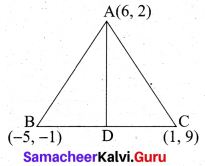
Mid point of BC(D) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
\(=\left(\frac{-5+1}{2}, \frac{-1+9}{2}\right)\)
\(=\left(\frac{-4}{2}, \frac{8}{2}\right)\) = (-2, 4)
Equation of the median AD is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
\(\frac{y-2}{4-2}=\frac{x-6}{-2-6}\)
\(\frac{y-2}{2}=\frac{x-6}{-8}\)
= 2(x – 6) = 8(y – 2)
2x – 12 = -8y + 16
2x + 8y – 28 = 0
(÷by 2) x + 4y – 14 = 0
(ii) To find the equation of the altitude
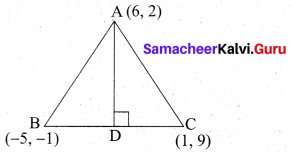
Slope of BC = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(=\frac{9+1}{1+5}\)
\(=\frac{10}{6}=\frac{5}{3}\)
Slope of the altitude = \(-\frac{3}{5}\)
Equation of the altitude AD is
y – y1 = m(x – x1)
y – 2 = \(-\frac{3}{5}\)(x – 6)
-3 (x – 6) = 5 (y – 2)
-3x + 18 = 5y – 10
-3x – 5y + 18 + 10 = 0
-3x – 5y + 28 =0
3x + 5y – 28 = 0
∴ Equation of the median is x + 4y – 14 = 0
Equation of the altitude is 3x + 57 – 28 = 0
![]()
Question 37.
Two ships are sailing in the sea on either sides of a lighthouse. The angle of elevation of the top of the lighthouse as observed from the ships are 30° and 45° respectively. If the lighthouse is 200 m high, find the distance between the two ships. (√3 = 1.732 )
Answer:
Let AB be the lighthouse. Let C and D be the positions of the two ships.
Then, AB = 200 m
∠ACB = 30°, ∠ADB = 45°
In right triangle BAC, tan 30° = \(\frac{A B}{A C}\)

\(\frac{1}{\sqrt{3}}=\frac{200}{\mathrm{AC}}\) gives AC = 200√3
In right triangle BAD, tan 45° = \(\frac{A B}{A D}[latex]
1 = [latex]\frac{200}{\mathrm{AD}}\) gives AD = 200
Now, CD = AC + AD = 200√3 + 200 [by (1) and (2)]
CD = 200 (√3 + 1) = 200 × 2.732 = 546.4
Distance between two ships is 546.4 m
Question 38.
Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Answer:
Radius of the cylinder = \(\frac{4.5}{2} \mathrm{cm}\)
Height of the cylinder = 10 cm
Volume of the cylinder = π r2 h cu. units
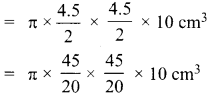
Radius of the coin (r) .= \(\frac{1.5}{2} \mathrm{cm}\)
Thickness of the coin (h) = 2 mm = \(\frac{2}{10} \mathrm{cm}\)
Volume of one coin = π r2 h cu. units
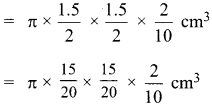

Number of coins = 450
![]()
Question 39.
A box contains cards numbered 3, 5, 7, 9, … 35, 37. A card is drawn at random from the box. Find the probability that the drawn card have either multiples of 7 or a prime number.
Answer:
Sample space = {3, 5, 7,9 ,… ,35, 37} \(\left[\frac{37-1}{2}=\frac{36}{2}=18\right]\)
n (S) = 18
Let A be the event of getting a multiple of 7
A = {7,21,35}
n(A) = 3
p(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{18}\)
‘ Let B be the event of getting a prime number
B = {3,5, 7, 11, 13, 17, 19, 23.29,31.37}
n (B) = 11
p(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{11}{18}\)
A∩B = {7}
n(A ∩ B) = 1
P(A ∩ B) = \(\frac{n(\mathrm{A} \cap \mathrm{B})}{n(\mathrm{S})}=\frac{1}{18}\)
p(A∪B) = P(A) + P(B) – P(A ∩ B)
\(=\frac{3}{18}+\frac{11}{18}-\frac{1}{18}=\frac{3+11-1}{18}=\frac{13}{18}\)
Probability of getting a muliple of 7 or a priime number = \(\frac{13}{18}\)
Question 40.
Find X and Y if X – Y = \(\left[ \begin{matrix} 2 & 1 \\ 4 & 3 \\ 0 & 6 \end{matrix} \right]\) and X + Y = \(\left[ \begin{matrix} 12 & 13 \\ 6 & 5 \\ 4 & 8 \end{matrix} \right] \)
Answer:

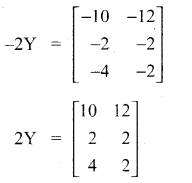
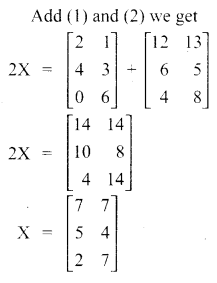
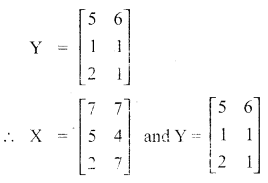
![]()
Question 41.
A lead pencil is in the shape of a right circular cylinder. The pencil is 28 cm long and its radius is 3 in. If the led is of radius one mm (1 mm) then find the volume of the wood used in the pencil.
Answer:
Length of a pencil (h) = 28 cm
Radius of a pencil (R) = 3mm \(\left(\frac{3}{10} \mathrm{cm}\right)\)
Radius of a led (r) = 1 mm \(\left(\frac{1}{10} \mathrm{cm}\right)\)
Volume of the wood used = Volume of the pencil – Volume of the led
= πh(R2 – r2cu. unit

Volume of the wood used in the pencil = 7.04 cm3
Question 42.
The following table shows the marks obtained by 48 students in a quiz competition in Mathematics. Calculate the variance and standard deviation.

Answer:
Let us form the following table using the given data.
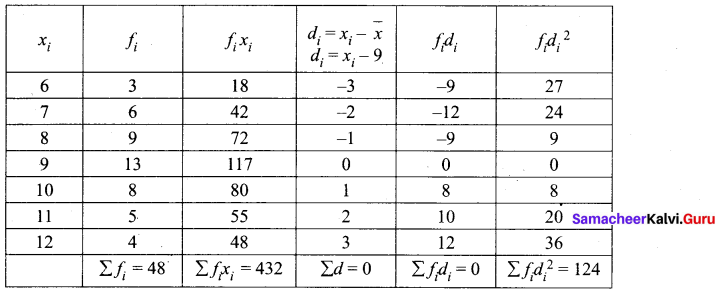

![]()
PART – IV
IV. Answer all the questions. [2 × 8 = 16]
Question 43.
(a) Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem. Rough Diagram
Answer:
Radius of the circle = 4.5 cm
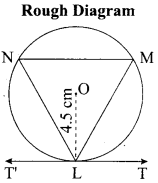
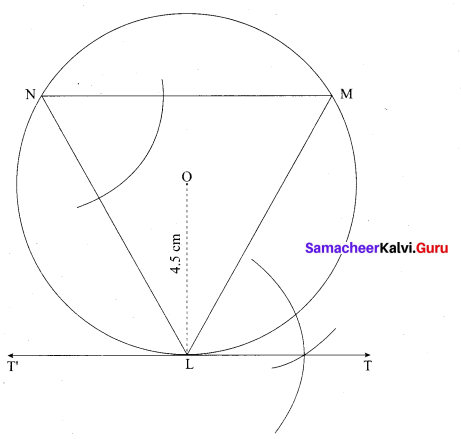
Steps of construction:
- With O as centre, draw a circle of radius 4.5 cm.
- Take a point L on the circle. Through L draw any chord LM.
- Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
- Through “L” draw tangent TT’ such that ∠TLM = ∠MNL.
- TT’ is the required tangent.
![]()
[OR]
(b)
Construct a ∆PQR in which QR = 5 cm, ∠P = 40° and the median PG from P to QR is 4.4 cm. Find the length of the altitude from P to QR.
Answer:
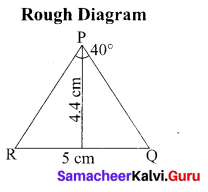
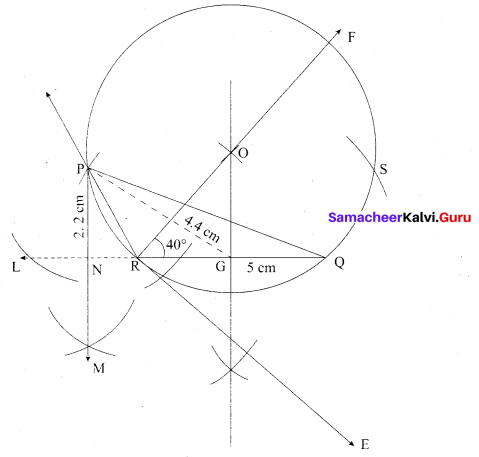
Steps of construction
- Draw a line segment RQ = 5 cm.
- At R draw RE such that ∠QRE = 40°.
- At R. draw RF such that ∠ERF = 90°.
- Draw the perpendicular bisector to RQ, which intersects RF at O and RQ at G.
- With O as centre and OP as radius draw a circle.
- From G mark arcs of radius 4.4 cm on the circle. Mark them as P and S.
- Join PR and PQ. Then ∆PQR is the required triangle.
- From P draw’ a line PN which is perpendicular to RQ it meets at N.
- Measure the altitude PN.
PN = 2.2 cm.
![]()
Question 44.
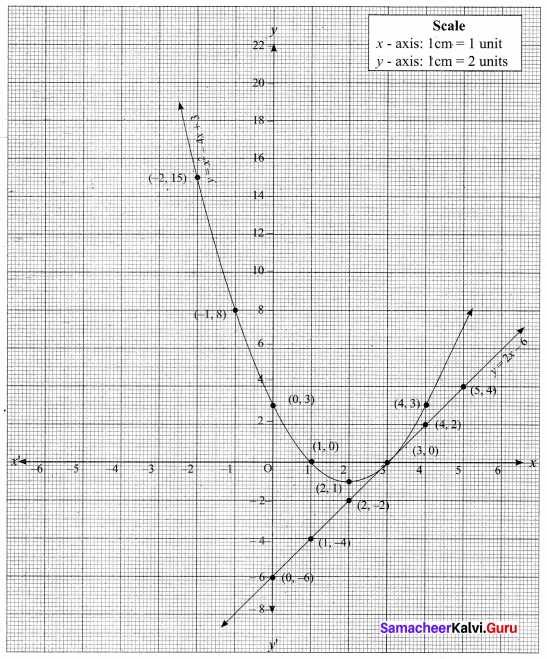
(a) Draw the graph of y = x2 – 4x + 3 and use it to solve x2 – 6x + 9 = 0.
Answer:
Step 1: Draw the graph of y = x2 – 4x + 3 by preparing the table of values as below.

Step 2: To solve x2 – 6x + 9 = 0, subtract x2 – 6x + 9 = 0 from y = – x2 – 4x + 3
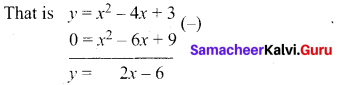
The equation y = 2x – 6 represent a straight line. Draw the graph of y = 2x – 6 form in the table of values as below.

The line y = 2x – 6 intersect y = x2 – 4x + 3 only at one point.
Step 3: Mark the point of intersection of the curve y = x2 – 4.r 3 and y = 2x – 6 that is (3,0).
Therefore, the x coordinate 3 is the only solution for the equation x2 – 6x + 9 = 0.
[OR]
![]()
(b) Draw the Graph of y = x2 – 4x + 4
Answer:
Let y = x2 – 4x + 4
(i) Prepare the table of values for y = x2 – 4x + 4
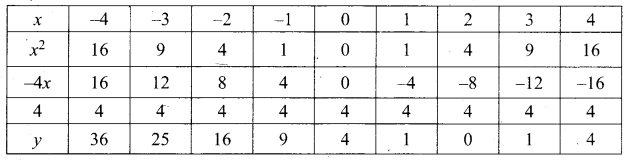
(ii) Plot the points (-3, 25) (-2, 16) (-1, 9) (0, 4) (1, 1) (2, 0), (3, 1) and (4, 4)
(iii) Join the points by a free hand smooth curve.
(iv) The roots of the equation are the X-coordinates of the intersecting points of the curve with X-axis (2, 0) which is 2.
(v) Since there is only one point of intersection with X-axis (2, 0).
The solution set is 2.
∴ The Quadratic equation x2 – 4x + 4 = 0 has real and equal roots. 1 English Medium – 33″ width=”573″ height=”72″ />
The line y = 2x – 6 intersect y = x2 – 4x + 3 only at one point.
Step 3: Mark the point of intersection of the curve y = x2 – 4.r 3 and y = 2x – 6 that is (3,0).
Therefore, the x coordinate 3 is the only solution for the equation x2 – 6x + 9 = 0.
