Samacheer Kalvi 9th Maths Guide Chapter 7 அளவியல் Ex 7.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.1 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 7 அளவியல் Ex 7.1

கேள்வி 1.
ஹெரான் சூத்திரத்தைப் பயன்படுத்தி பின்வரும் பக்க அளவுகளைக் கொண்டமுக்கோணத்தின் பரப்பைக் காண்க.
i) 10செ.மீ. 24செ.மீ, 26செ.மீ.
ii) 1.8 மீ, 8மீ, 8.2மீ
விடை:
i) 10செ.மீ. 24செ.மீ, 26செ.மீ.
a = 10 செ.மீ, b = 24 செ.மீ, c = 26 செ.மீ.
s = \(\frac{a+b+c}{2}\)
s = \(\frac{10+24+26}{2}\) = \(\frac{60}{2}\)
s = 30
முக்கோணத்தின் பரப்பளவு
= \(\sqrt{s(s-a)(s-b)(s-c)}\) ச. அலகுகள்
= \(\sqrt{30(30-10) 30-24)(30-26)}\) ச. அலகுகள்
= \(\sqrt{30 \times 20 \times 6 \times 4}\) ச. அலகுகள்
= \(\sqrt{3 \times 10 \times 2 \times 10 \times 2 \times 3 \times 2 \times 2}\) ச. அலகுகள்
= 3 × 10 × 2 × 2
= 120 செ.மீ²

ii) 1.8 மீ, 8 மீ, 8.2 மீ
a = 1.8 மீ, b = 8 மீ, c = 8.2 மீ
s = \(\frac{a+b+c}{2}\)
s = \(\frac{1.8+8+8.2}{2}\) = \(\frac{18}{2}\)
s = 9 மீ
முக்கோணத்தின் பரப்பளவு
= \(\sqrt{s(s-a)(s-b)(s-c)}\) ச. அலகுகள்
= \(\sqrt{9 \times(9-1.8)(9-8)(9-8.2)}\) ச. அலகுகள்
= \(\sqrt{9 \times 7.2 \times 1 \times 0.8}\) மீ²
= \(\sqrt{51.84}\) மீ²
= 7.2 மீ²

கேள்வி 2.
ஒரு முக்கோண வடிவ நிலத்தின் பக்கங்கள் முறையே 22மீ, 120மீ மற்றும் 122மீ எனில் வயலின் பரப்பளவைக் கணக்கிடுக. மேலும் வயலைச் சமப்படுத்த ஒரு சதுர மீட்டருக்கு ₹20 செலவாகும் எனில், வயலைச் சமப்படுத்த ஆகும் மொத்தச் செலவைக் கணக்கிடுக.
விடை:
a = 22மீ, b = 120மீ, c = 122e
s = \(\frac{a+b+c}{2}\)
s = \(\frac{22+120+122}{2}\) = \(\frac{264}{2}\)
s = 132
முக்கோண வடிவ நிலத்தின் பரப்பளவு
= \(\sqrt{s(s-a)(s-b)(s-c)}\) ச. அலகுகள்
= \(\sqrt{132(132-22)(132-120)(132-122)}\) ச. அ
= \(\sqrt{132 \times 110 \times 12 \times 10}\) ச. அலகுகள்
= \(\sqrt{12 \times 11 \times 11 \times 10 \times 12 \times 10}\) ச. அலகுகள்
= 12 × 11 × 10
= 1320 மீ²
வயலைச் சமப்படுத்த 1ச.மீ.க்கு ஆகும் செலவு = ரூ.20
வயலைச் சமப்படுத்த 1320ச.மீ.க்கு ஆகும் செலவு = ரூ.20 × 1320 = ரூ. 26,400.

கேள்வி 3.
ஒரு முக்கோண வடிவிலான மனையின் சுற்றளவு GOOமீ. அதன் பக்கங்கள் 5:12:13 என்ற விகிதத்தில் உள்ளன எனில் அந்த மனையின் பரப்பளவைக் காண்க.
விடை:
விகிதம் = 5:12 : 13
முக்கோணத்தின் பக்க அளவுகளை 5K, 12K மற்றும் 13K என்க.
சுற்றளவு = 600 மீ
5K + 12K + 13K = 600 மீ
30K = 600 மீ
K = \(\frac{600}{30}\)
K = 20 மீ
பக்கங்கள்
a = 100 மீ
b = 240 மீ
c = 260 மீ
s = \(\frac{a+b+c}{2}\)
s = \(\frac{100+240+260}{2}\) = \(\frac{600}{2}\)
s = 300 மீ.
மனையின் பரப்பளவு
= \(\sqrt{s(s-a)(s-b)(s-c)}\) ச. அலகுகள்
= \(\sqrt{300(300-100)(300-240)(300-260)}\) ச. அ.
= \(\sqrt{300 \times 200 \times 60 \times 40}\) ச. அலகுகள்
= \(\sqrt{144000000}\) ச. அலகுகள்
= 12000 மீ²

கேள்வி 4.
180 செ.மீ. சுற்றளவு கொண்ட ஒரு சமபக்க முக்கோணத்தின் பரப்பளவைக் காண்க.
விடை:
சுற்றளவு = 180 செ.மீ.
சமபக்க முக்கோணத்தின் பரப்பளவு = \(\frac{\sqrt{3}}{4}\) a²
a + b + c = 180
a + a + a = 180 (அனைத்து பக்கங்களும் சமம்)
3a = 180
a = \(\frac{180}{3}\)
a = 60 செ.மீ.
சமபக்க முக்கோணத்தின் பரப்பளவு
= \(\frac{\sqrt{3}}{4}\) a² ச.அலகுகள்
= \(\frac{\sqrt{3}}{4}\) × 60² செ.மீ.²
= \(\frac{\sqrt{3}}{4}\) × 3600 செ.மீ.²
= \(\sqrt{3}\) × 900 செ.மீ.²
= 1.732 × 900 செ.மீ.²
= 1558.8 செ.மீ.²

கேள்வி 5.
இரு சமபக்க முக்கோண வடிவிலுள்ள ஒரு விளம்பரப் பலகையின் சுற்றளவு 36மீ மற்றும் அதன் ஒவ்வொரு சமபக்கத்தின் நீளம் 13மீ ஆகும். அதற்கு வண்ண ம் பூச ஒரு சதுர மீட்டருக்கு ₹ 17.50 வீதம் ஆகும் செலவைக் காண்க.
விடை:
சுற்றளவு = 36 மீ
a + b + c = 36
a = 13மீ, b = 13மீ, c = 10மீ
s = \(\frac{a+b+c}{2}\)
s = \(\frac{13+13+10}{2}\) = \(\frac{36}{2}\)
s = 18 மீ
இருசமபக்க முக்கோணத்தின் பரப்பளவு

ஒரு ச.மீ. வண்ண ம் பூச ஆகும் செலவு
= ரூ.17.50
60 சமீ. வண்ண ம் பூச ஆகும் செலவு
= ரூ.17.50 × 60
= ரூ. 1050.00
= ரூ. 1050

கேள்வி 6.
படத்தில் நிழலிடப்படாத பகுதியின் பரப்பளவைக் காண்க.

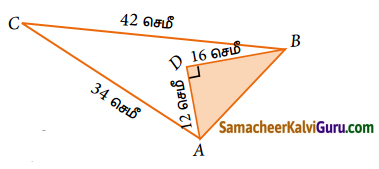
விடை:
∆ ABD
AB² = AD² + DB²
= (12)² + (16)²
= 144 + 256
= 400
AB = \(\sqrt{400}\)
AB = 20செ.மீ., a = 20செ.மீ., b = 12செ.மீ., c = 16செ.மீ.
s = \(\frac{a+b+c}{2}\)
s = \(\frac{12+16+20}{2}\) = \(\frac{48}{2}\)
s = 24 செ.மீ.
∆ ABD இன் பரப்பளவு
= \(\sqrt{s(s-a)(s-b)(s-c)}\) ச. அலகுகள்
= \(\sqrt{24(24-12)(24-16)(24-20)}\) செ.மீ.²
= \(\sqrt{24 \times 12 \times 8 \times 4}\) செ.மீ.²
= \(\sqrt{12 \times 2 \times 12 \times 4 \times 2 \times 4}\) செ.மீ.²
= 12 × 4 × 2 செ.மீ.²
= 96 செ.மீ.²

∆ ABC இல், a = 20செ.மீ. b = 34செ.மீ., c = 42செ.மீ.
s = \(\frac{a+b+c}{2}\)
s = \(\frac{20+34+42}{2}\) = \(\frac{96}{2}\)
s = 48 செ.மீ.
∆ ABC இன் பரப்பளவு

= 6 × 2 × 2 × 14 செ.மீ.²
= 336 செ.மீ.²
நிழலிடப்படாத பகுதியின் பரப்பளவு
= ∆ABC இன் பரப்பளவு – ∆ ABD இன்
பரப்பளவு
= 336 செ.மீ.² – 96 செ.மீ.²
= 240 செ.மீ.²

கேள்வி 7.
AB = 13 செ. மீ.., BC = 12 செ.மீ., CD = 9செ.மீ. AD = 14 செ.மீ. ஆகியவற்றைப் பக்கங்களாகவும் BD = 15 செ.மீ. ஐ மூலைவிட்டமாகவும் கொண்ட நாற்கரம் ABCD இன் பரப்பைக் காண்க.
விடை:
நாற்கரம் ABCD இல், BD என்ற மூலைவிட்டத்தை இணைக்க,
a = 13செ.மீ., b = 14செ.மீ., c = 15செ.மீ.
∆ ABD இல்
∆ ABD இன் பரப்பளவு,

= 7 × 3 × 2 × 2 செ.மீ.²
= 84 செ.மீ.²
∆ BCD இல்,
a = 9செ.மீ., b = 12செ.மீ., c = 15செ.மீ.

= 9 × 2 × 3 செ.மீ.²
= 54 செ.மீ.²
நாற்கரத்தின் பரப்பளவு
= ∆ ABD இன் பரப்பளவு + ∆ BCD இன் பரப்பளவு
= 84 செ.மீ.² + 54 செ.மீ.²
= 138 செ.மீ.²

கேள்வி 8.
ஒரு பூங்காவானது நாற்கர வடிவிலுள்ளது. அந்தப் பூங்காவின் பக்க அளவுகள் முறையே 15மீ , 20மீ , 26மீ மற்றும் 17மீ மற்றும் முதல் இரண்டு பக்கங்களுக்கு இடையேயுள்ள கோணம் செங்கோணம் எனில் பூங்காவின் பரப்பைக் காண்க.
விடை:
நாற்கரம் ABCD இல் BD என்ற மூலைவிட்டத்தை இணைக்க.

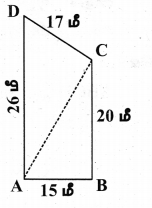
∆ ABC இன் பரப்பளவு
= \(\frac{1}{2}\) × b × h ச. அலகுகள்
= \(\frac{1}{2}\) × 15 × 20 செ.மீ.²
= 150 செ.மீ.²
பிதாகரஸ் தேற்றத்தின் படி, செங்கோண முக்கோணம் ABC இல்
AC² = (15)² + (20)²
= 225 + 400
= 625
AC = \(\sqrt{625}\)
= 25 மீ.
∆ ACD இல் a = 25மீ. b = 26e. c = 17மீ.
s = \(\frac{a+b+c}{2}\)
s = \(\frac{25+26+17}{2}\) = \(\frac{68}{2}\)
s = 34மீ.
∆ ACD இன் பரப்பளவு
= \(\sqrt{\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}\) ச. அலகுகள்
= \(\sqrt{34 \times(34-25)(34-26)(34-17)}\) மீ²
= \(\sqrt{34 \times 9 \times 8 \times 17}\) மீ²
= \(\sqrt{17 \times 2 \times 3 \times 3 \times 2 \times 2 \times 2 \times 17}\) மீ²
= 17 × 3 × 2 × 2 மீ²
= 204 மீ²
நாற்கரம் ABCD இன் பரப்பளவு
= ∆ ABC இன் பரப்பளவு + ∆ ACD இன் பரப்பளவு
= 150 மீ² + 204 மீ²
= 354 மீ²

கேள்வி 9.
ஒரு நிலமானது சாய்சதுர வடிவில் உள்ளது. நிலத்தின் சுற்றளவு 160மீ மற்றும் அதன் ஒரு மூலைவிட்டத்தின் அளவு 48மீ எனில் அந்த நிலத்தின் பரப்பைக் காண்க.
விடை:
ABCD ஒரு சாய்சதுரம் என்க.

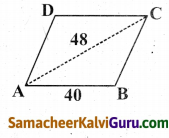
சுற்றளவு = 160 மீ
4a = 160 மீ
a = \(\frac{160}{4}\) மீ
a = 40 மீ)
மூலைவிட்டம் AC இன் நீளம் = 48மீ
∆ ABC இல், a = 40மீ, b = 40மீ, c = 48மீ

= 8 × 24 × 4
= 768 மீ
நிலத்தின் பரப்பளவு = 2 × ∆ ABC இன் பரப்பளவு
= 2 × 768 மீ²
= 1536 மீ²

கேள்வி 10.
ஒர் இணைகரத்தின் அடுத்தடுத்த பக்கங்களின் அளவுகள் 34மீ, 20மீ மற்றும் அதன் ஒரு மூலைவிட்டத்தின் அளவு 42 மீ எனில் அந்த இணைகரத்தின் பரப்பைக் காண்க.
விடை:
மூலைவிட்டத்தின் நீளம் = 42 மீ.
∆ ABC இல், a = 34மீ, b = 20மீ, c = 42மீ

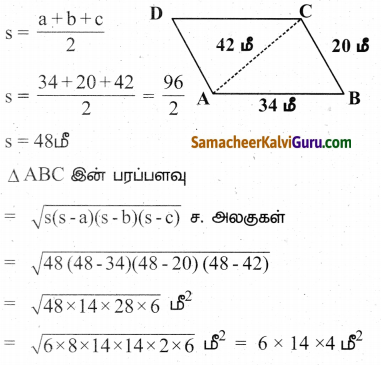
= 84 × 4 மீ²
= 336 மீ²
இணைகரத்தின் பரப்பளவு = 2 × ∆ ABC இன் பரப்பளவு
= 2 × 336 மீ.²
= 672 மீ²