Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 4 வடிவியல் Ex 4.1 Textbook Questions and Answers, Notes.
TN Board 9th Maths Solutions Chapter 4 வடிவியல் Ex 4.1
கேள்வி 1.
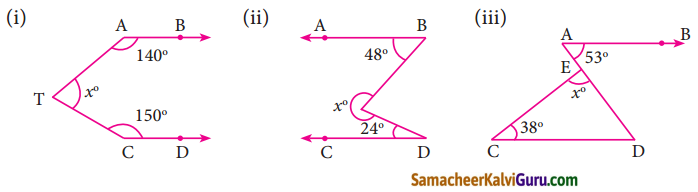
படத்தில் AB ஆனது CD க்கு இணை எனில், x இன் மதிப்புக் காண்க.
விடை:
(i) AB||CD
\(\lfloor A T C+\lfloor B A T+\lfloor T C D\) = 360°
x + 140°+ 150°= 360°
x + 290°= 360°
x = 360° – 290°
x = 70°
(ii) \(\lfloor A B T+\lfloor B T D+\lfloor T D C\) = 360°
48° + x + 24° = 360°
x + 72° = 360°
x = 360° – 72°
x = 288°
(iii) AB || CD
∠E + ∠C + ∠D = 180° (முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180°)
x + 38° + 53° = 180°
x + 91° = 180°
x = 180° – 91°
x = 89°
![]()
கேள்வி 2.
ஒரு முக்கோணத்தின் கோணங்களின் விகிதம் 1 : 2 : 3, எனில் முக்கோணத்தின் ஒவ்வொரு கோண அளவைக் காண்க.
விடை:
முக்கோணத்தின் கோணங்களை முறையே x, 2x ,3x என்க
கணக்கின் படி,
x + 2x + 3x = 180° ( முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180°)
6x = 180°
x = \(\frac{180}{6}\)
x = 30°
2x = 2 × 30°
= 60°
3x = 3 × 30°
= 90°
மூன்று கோணங்கள் = 30°, 60°, 90°
கேள்வி 3.
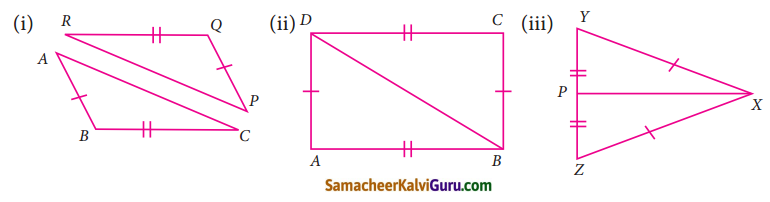
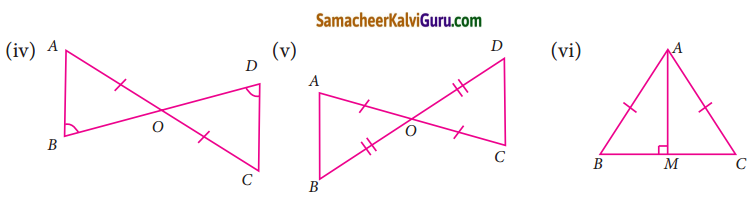
கொடுக்கப்பட்டுள்ள முக்கோணச் சோடிகளைக்கருத்தில் கொள்க. மேலும் அவற்றில் ஒவ்வொரு சோடியும் சர்வசம முக்கோணங்களா எனக் காண்க. அவை சர்வசம முக்கோணங்கள் எனில் எப்படி? இல்லையெனில் அவை சர்வசமமாக என்ன செய்ய வேண்டும்?
விடை:
(i) AB = PQ
BC = QR
ΔABC ≅ ΔPQR
(ii) AB = CD
BC = AD
ΔABD ≅ ΔBCD
(iii) XY = XZ
YP = PZ
ΔXYP ≅ ΔXZP
(iv) OA = OC
∠OBA = ∠ODC
ΔOAB ≅ ΔOCD
(v) OA = OC
OB = OD
ΔOAB ≅ OCD
(vi) AB = AC
ΔAMB ≅ AMC
![]()
கேள்வி 4.
ΔABC மற்றும் ΔDEF இல் AB = DF, மற்றும் ∠ACB =70°, ∠ ABC = 60°; ∠ DEF = 70° மற்றும் ∠EDF = 60° எனில் முக்கோணங்கள் சர்வசமம் எனக் காட்டுக.
விடை:
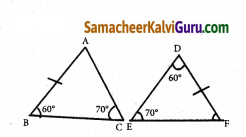
AB = DF (தரவு)
ஒரு முக்கோணத்தின் இரு கோணங்களும் அதன் ஏதாவது ஒரு பக்கமும் மற்றொரு முக்கோணத்தின் இரு கோணங்களுக்கும், ஒத்த பக்கத்திற்கும் சமம் எனில், அவ்விரு முக்கோணங்களும் சர்வ சமம் ஆகும் (கோ – கோ – ப)
∴ ΔABC ≅ ΔDEF
கேள்வி 5.
கொடுக்கப்பட்ட AABC இல் அனைத்துக் கோண அளவுகளையும் காண்க
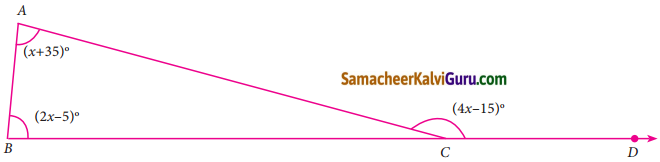
விடை:
படத்திலிருந்து
\(\lfloor A+\lfloor\underline{B}=\lfloor C\)
முக்கோணத்தின் ஒரு பக்கம் நீட்டப்பட்டால் உண்டாகும் வெளிக்கோணமானது இரண்டு உள்ளெதிர்க் கோணங்களின் கூடுதலுக்குச் சமம்
x + 35° + 2x – 5 = 4x – 15
x + 2x + 35 – 5 = 4x – 15
3x + 30 = 4x – 15
30 + 15 = 4x – 3x
45 = x
x = 45°
\(\lfloor A\) = x + 35°
\(\lfloor A\) = 45° + 35
\(\lfloor A\) = 80°
\(\lfloor B\) = 2x – 5°
\(\lfloor B\) = 2 × 45° – 5°
\(\lfloor B\) = 90° – 5°
\(\lfloor B\) = 85°
\(\lfloor C\) = 4x – 15°
= 4 × 45° – 15°
\(\lfloor C\) = 180° – 15°
\(\lfloor C\) = 1650