Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.14 Textbook Questions and Answers, Notes.
TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.14
கேள்வி 1.
ஓர் ஈரிலக்க எண்ணையும் அதன் இலக்கங்களை மாற்றுவதால் கிடைக்கும் எண்ணையும் கூட்டினால் 110 கிடைக்கும். கொடுக்கப்பட்ட அந்த ஈரிலக்க எண்ணிலிருந்து 10 ஐக் கழித்தால் அது கொடுக்கப்பட்ட ஈரிலக்க எண்ணின் இலக்கங்களின் கூடுதலின் 5 மடங்கை விட 4 அதிகம் எனில் அந்த எண்ணைக் காண்க.
விடை:
பத்தாம் இலக்க இடத்தில் இருக்கும் எண்ணை x என்க.
10x + y ………………..(1)
இலக்கங்கள் இடமாறுதல் அடையும்போது
x + 10y …………………(2)
கணக்கின் படி,
10x + y +x + 10y = 110
11x + 11y = 110
x + y = 10 …………………(3)
கணக்கின் படி,
10x + y – 10 = 5(x + y) + 4
10x + y – 10 = 5x + 5y + 4
10x + y – 5x – 5y= 4 + 10
5x – 4y = 14 ………………..(4)
x + y = 10
5x – 4y = 14
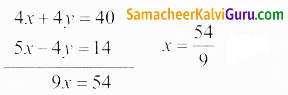
x = 6
x = 6 என (3) இல் பிரதியிடுக
x + y = 10
6 + y = 10
y = 10 – 6
y = 4
∴ முதல் எண் = 10x + y
= 10 x 6 +4
= 60 + 4 = 64
கேள்வி 2.
ஒரு பின்னத்தின் பகுதி மற்றும் தொகுதியின் கூடுதல் 12. அப்பின்னத்தின் பகுதியுடன் 3 ஐக் கூட்டினால் அதன் மதிப்பு \(\frac { 1 }{ 2 }\) ஆகும் எனில் அப்பின்னத்தைக் காண்க.
விடை:
பின்னத்தை \(\frac { x }{ y }\) என்க.
கணக்கின் படி, x + y = 12………………(1)
\(\frac{x}{y+3}=\frac{1}{2}\)
2x = y + 3
2x – y = 3 ………………….(2)
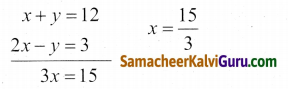
x = 5
x = 5 என (1) இல் பிரதியிடுக.
x + y = 12
5 + y = 12
y = 12 – 5
y = 7
பின்னம் \(=\frac{x}{y}=\frac{5}{7}\)
![]()
கேள்வி 3.
ABCD என்ற வட்ட நாற்கரத்தில் ∠A = (4y + 20)°, ∠B = (3y – 5)° , ∠C = (4x)° மற்றும் ∠D = (7x + 5)° எனில் நான்கு கோணங்களையும் காண்க.
விடை:
ஒரு வட்ட நாற்கரத்தில் எதிர்க்கோணங்களின் கூடுதல் 180°
∠A + ∠C=180°
(4y + 20) ° + 4x° = 180°
4x + 4y = 160°
x + y = 40 ………………..(1)
∠B + ∠D=180°
(3y – 5)° + (7x + 5) = 180°
7x + 3y + 5 – 5 = 180°
x + y = 40
7x + 3y = 180
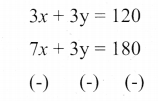
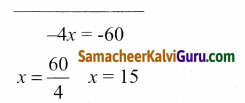
x = 15 என (1) இல் பிரதியிடுக.
x + y = 40
15 + y = 40
y = 40 – 15
y = 25
∠A = 4y + 20
= 4 × 25 + 20
= 100° +20
∠A = 120°
∠B = 3y – 5
= 3 × 25 – 5
= 75 – 5
∠B = 70°
∠C = 4x
= 4 × 15
∠C = 60°
∠D = 7x + 5
= 7 × 15° + 5
= 105 + 5
∠D = -110°
கேள்வி 4.
ஒரு தொலைக்காட்சிப் பெட்டியை 5% இலாபத்திற்கும், ஒரு குளிர்சாதனப் பெட்டியை 10% இலாபத்திற்கும் விற்பதால் கடைக்காரருக்கு நிகர இலாபம் ₹2000 கிடைக்கிறது. ஆனால் அவர் ஒரு தொலைக்காட்சிப் பெட்டியை 10% இலாபத்திற்கும், ஒரு குளிர்சாதனப் பெட்டியை 5% நட்டத்திற்கும் விற்பதால் அவரின் நிகர இலாபம் ₹1500 கிடைக்கிறது எனில், தொலைக்காட்சிப் பெட்டி மற்றும் குளிர்சாதனப் பெட்டியின் சரியான விலைகளைக் காண்க.
விடை:
தொலைக்காட்சிப் பெட்டியின் சரியான விலை = ரூ. x என்க.
குளிர்சாதனப் பெட்டியின் சரியான விலை = ரூ. y என்க.

y = 10000 என (1) இல் பிரதியிடுக.
x + 2y = 40000
x + 2 × 10000 = 40000
x + 20000 = 40000
x = 40000 – 20000
x = 20000
தொலைக்காட்சிப்பெட்டியின் விலை = ரூ.20,000.
குளிர்சாதனப்பெட்டியின் விலை = ரூ. 10,000.
![]()
கேள்வி 5.
இரு எண்கள் 5:6 என்ற விகிதத்தில் உள்ளன. அவை ஒவ்வொன்றிலிருந்தும் முறையே 8 ஐக் கழித்தால் அவற்றின் விகிதம் 4:5 என மாறும் எனில், அந்த எண்களைக் காண்க.
விடை:
விகிதம் = 5:6
அந்த எண்கள் x, y என்க.
x : y = 5 : 6
\(\frac{x}{y}=\frac{5}{6}\) …………….. (1)
\(\frac{x-8}{y-8}=\frac{4}{5}\) …………..(2)
6x = 5y
(1) ⇒ 6x – 5y = 0
(2) ⇒ 5(x – 8) = 4(y – 8)
5x – 40 = 4y – 32
5x – 4y = 8

y = 48
y = 48 என (1) இல் பிரதியிடுக.
6x – 5y = 0
6x – 5 × 48 = 0
6x = 240
x = \(\frac{240}{6}\)
x = 40
அந்த எண்கள் : x = 40, y = 48
கேள்வி 6.
4 இந்தியர்கள் மற்றும் 4 சீனர்கள் சேர்ந்து 3 நாள்களில் ஒரு வேலையை முடிக்கிறார்கள். 2 இந்தியர்கள் மற்றும் 5 சீனர்கள் சேர்ந்து அதே வேலையை 4 நாள்களில் முடிக்கிறார்கள் எனில், இப்பணியைத் தனியாக ஒரு இந்தியர் எத்தனை நாள்களில் செய்வார்? ஒரு சீனர் தனியாக எத்தனை நாள்களில் செய்வார்?
விடை:
ஒரு இந்தியர் தனியாக இப்பணியை ஒரு நாளில் செய்வதை \(\frac { 1 }{ x }\) என்க.
ஒரு சீனர் தனியாக இப்பணியை ஒரு நாளில் செய்வதை = \(\frac { 1 }{ y }\) என்க.

y = 36
b = \(\frac{1}{36}\) என (2) இல் பிரதியிடுக.
2a + 5b = \(\frac{1}{4}\)
2a + 5\(\left(\frac{1}{36}\right)=\frac{1}{4}\)
2a = \(\frac{1}{4}-\frac{5}{36}\)
2a = \(\frac{9-5}{36}\)
2a = \(\frac{4}{36}\) 2a = \(\frac{1}{9}\)
a = \(\frac{1}{18}\)
x = 18
1 சீனர் = 36 நாட்கள்
1 இந்தியர் = 18 நாட்கள்