Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.11 Textbook Questions and Answers, Notes.
TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.11
கேள்வி 1.
பிரதியிடல் முறையில் காண்க.
(i) 2x – 3y = 7; 5x +y = 9
(ii) 1.5x + 0.1y = 6.2; 3x – 0.4y = 11.2
(iii) x இல்10% + y இல் 20% = 24; 3x – y = 20
(iv) √2x – √3y = 1;√3x – √8y = 0
குறிப்பு : \(\frac{1}{\sqrt{x}}\) = a; \(\frac{1}{\sqrt{y}}\) = b) என்க
தீர்வு : (i) 2x – 3y = 7 ………………(1)
5x + y = 9 ……………… (2)
(2) இலிருந்து
5x + y = 9
y = 9 – 5x ……. (3)
(3) ஐ (1) இல் பிரதியிடுக
2x – 3y = 7
2x – 3 × (9 – 5x) = 7
2x – 27 + 15x = 7
17x = 7 + 27
17x = 34
x = \(\frac{34}{17}\)
x = 2
x = 2 என (2) இல் பிரதியிடுக
5x + y = 9
5 × 2 + y = 9
10 + y = 9
y = 9 – 10
y = -1
(ii) 1.5x + 0.1y = 6.2 ……………….(1)
3x – 0.4y = 11.2 …………………….(2)
(2) இலிருந்து
3x = 11.2 + 0.4y
x = \(\frac{11.2+0.4 y}{3}\) ……………….(3)
(3) ஐ (1) இல் பிரதியிடுக
1.5x + 0.1y = 6.2

16.8 + 0.6y +0.3y = 18.6
16.8 +0.9y = 18.6
0.9y = 18.6 – 16.8
0.9y = 1.8
y = \(\frac{1.8}{0.9}\)
y = \(\frac{18}{9}\)
y = 2
y = 2 என (2) இல் பிரதியிட
3x – 0.4y = 11.2
3x – 0.8 = 11.2
3x = 11.2 + 0.8
3x = 12
x = \(\frac{12}{3}\)
x = 4
(iii) x இல் 10% + y இல் 20% = 24 …………………. (1)
3x – y = 20
\(\frac{10}{100} x+\frac{20}{100}\) y = 24 …………….. (1)
3x – y = 20 ………………. (2)
(2) இலிருந்து
3x – 20 = y
y = 3x – 20 என (1) இல் பிரதியிடுக
\(\frac{1}{10}\) x + \(\frac{1}{5}\) y = 24

x = 40
x = 40 என (2) இல் பிரதியிடுக
3x – y = 20
3 × 40 – y = 20
120 – y = 20
120- 20 = y
y = 100
(iv) √2x – √3y = 1 …………….. (1)
√3x – √8y = 0 ……………….. (2)
(2) இலிருந்து
√3x – √8y = 0
√3x = √8y
x = \(\frac{\sqrt{8}}{\sqrt{3}}\) y
x = \(\frac{\sqrt{8}}{\sqrt{3}}\) y என (1) இல் பிரதியிட
√2x – √3y = 1
√2 × \(\frac{\sqrt{8}}{\sqrt{3}}\) y – √3y = 1
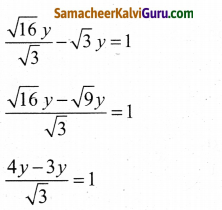
y = √3
y = √3 என (1) இல் பிரதியிடுக
√2x – √3y = 1
√2x – √3 × √3 = 1
√2x – 3 = 1
√2x = 1+3
√2x = 4
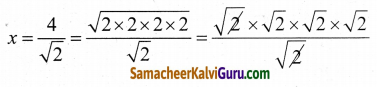
x = √8
![]()
கேள்வி 2.
இராமனின் வயது அவருடைய இரு மகன்களுடைய வயதுகளின் கூடுதலைப் போல் மூன்று மடங்காகும். ஐந்தாண்டுகள் கழித்து அவரின் வயது தனது மகன்களுடைய வயதுகளின் கூடுதலைப் போல் இரு மடங்காகும் எனில், இராமனின் தந்போதைய வயதைக் காண்க.
தீர்வு:
ராமனின் வயதை x ஆண்டுகள் என்க.
அவருடைய இரு மகன்களுடைய வயதை முறையே y மற்றும் z ஆண்டுகள் என்க.
x = 3 (y + z) ………………..(1)
ஐந்து வருடங்களுக்குப் பிறகு
5 + x = 2((y + 5) + (z + 5))
5 + x = 2y + 2z + 10 + 10
5+ x = 2y + 2z + 20
x = 2y + 2z + 20 – 5
3(y+z) = 2y + 2z + 15
3y + 3z = 2y + 2z + 15
y + z = 15
(1) இலிருந்து
x = 3 (y + z) = 3 × 15
x = 45
இராமனின் வயது = 45 ஆண்டுகள்
![]()
கேள்வி 3.
100 மற்றும் 1000 இக்கு இடையே அமையும் ஒரு மூன்றிலக்க எண்ணின் நடு இலக்கம் பூச்சியமாகவும் மற்ற இரு இலக்கங்களின் கூடுதல் 13 ஆகவும் இருக்கின்றன. இலக்கங்களை இடம் மாற்றி அமைக்கும்போது கிடைக்கும் எண்ணானது, அந்த எண்ணை விட 495 அதிகம் எனில், அந்த எண்ணைக் காண்க.
தீர்வு:
100ம் இலக்க இடத்தில் இருக்கும் எண்ணை x என்க.
ஒன்றாம் இலக்க இடத்தில் இருக்கும் எண்ணை y என்க .
அந்த எண் 100x + y
இரு இலக்கங்களின் கூடுதல் x + y = 13
இலக்கங்களை இடம் மாற்றி அமைக்கும் போது கிடைக்கும் புதிய எண் 100y + x
கணக்கின் படி
100x + y – (100y + x) = 495
100x + y – 100y – x = 495
99x – 99y = 495
x – y = 5
x + y = 13
2x = 18
x = 9
x= 9 என x + y = 13 இல் பிரதியிடுக
9 + y = 13
y = 13 – 9
y = 4
∴ அந்த எண் = 100y + x
= 100 × 4 +9
= 400 + 9
= 409