You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.2
9th Maths Exercise 2.2 Samacheer Kalvi Question 1.
Express the following rational numbers into decimal and state the kind of decimal expansion.
(i) \(\frac { 2 }{ 7 }\)
(ii) \(-5 \frac{3}{11}\)
(iii) \(\frac { 22 }{ 3 }\)
(iv) \(\frac { 327 }{ 200 }\)
Solution:
(i) \(\frac { 2 }{ 7 }\)
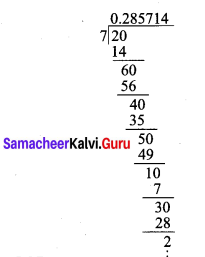
\(\frac{2}{7}=0 . \overline{285714}\)
Nen-terminating and recurring
(ii) \(-5 \frac{3}{11}\)
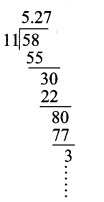
\(-5 \frac{3}{11}=-5 . \overline{27}\)
Nen-terminating and recurring
(iii) \(\frac { 22 }{ 3 }\)
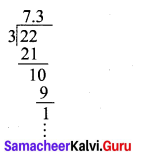
\(\frac{22}{3}=7 . \overline{3}\)
Nen-terminating and recurring
(iv) \(\frac { 327 }{ 200 }\)

\(\frac { 327 }{ 200 }\) = 1.635, Terminating.
9th Maths Exercise 2.2 In Tamil Question 2.
Express \(\frac { 1 }{ 13 }\) in decimal form. Find the length of the period of decimals.
Solution:
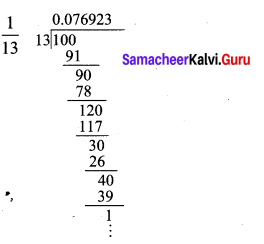
\(\frac{1}{13}=0 . \overline{076923}\) has the length of the period of decimals = 6.
9th Standard Maths Exercise 2.2 Question 3.
Express the rational number \(\frac { 1 }{ 13 }\) in recurring decimal form by using the recurring decimal expansion of \(\frac { 1 }{ 11 }\) . Hence write \(\frac { 71 }{ 33 }\) in recurring decimal form.
Solution:
The recurring decimal expansion of \(\frac { 1 }{ 11 }\) = 0.09090909…. = \(0.\overline { 09 }\)
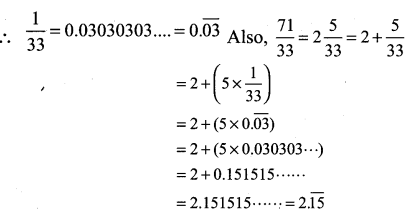
9th Maths Exercise 2.2 Question 4.
Express the following decimal expression into rational numbers.
(i) \(0.\overline { 24 }\)
(ii) \(2.\overline { 327 }\)
(iii) -5.132
(iv) \(3.1\overline { 7 }\)
(v) \(17.\overline { 215 }\)
(vi) \(-21.213\overline { 7 }\)
Solution:
(i) \(0.\overline { 24 }\)
Let x = \(0.\overline { 24 }\) = 0.24242424……… ….(1)
(Here period of decimal is 2, multiply equation (1) by 100)
100x = 24.242424 ………. ….(2)
(2) – (1)
100x – x = 24.242424…. – 0.242424….
99x = 24
x = \(\frac { 24 }{ 99 }\)
(ii) \(2.\overline { 327 }\)
Let x = 2.327327327…… …………. (1)
(Here period of decimal is 3, multiply equation (1) by 1000)
1000x = 2327.327… ……………. (2)
(2) – (1)
1000x – x = 2327.327327… – 2.327327….
999x = 2325
x = \(\frac { 2325 }{ 999 }\)
(iii) -5.132
\(x=-5.132=\frac{-5132}{1000}=\frac{-1283}{250}\)
(iv) \(3.1\overline { 7 }\)
Let x = 3.1777 ……. ………… (1)
(Here the repeating decimal digit is 7, which is the second digit after the decimal point, multiply equation (1) by 10)
10x = 31.7777 …….. …………. (2)
(Now period of decimal is 1, multiply equation (2) by 10)
100x = 317.7777…….. …………….. (3)
(3) – (2)
100x – 10x = 317.777…. – 31.777….
90x = 286
\(x=\frac{286}{90}=\frac{143}{45}\)
(v) \(17.\overline { 215 }\)
Let x = 17.215215 ……. ………. (1)
1000x = 17215.215215…… …………. (2)
(2) – (1)
1000x – x = 17215.215215… – 17.215…
999x = 17198
x = \(\frac { 17198 }{ 999 }\)
(vi) \(-21.213\overline { 7 }\)
Let x = -21.2137777… ……….. (1)
10x = -212.137777…… ……….. (2)
100x = -2121.37777…… ………… (3)
1000x = -21213.77777…. ……….. (4)
10000x = 212137.77777….. ………… (5)
(Now period of decimal is 1, multiply equation (4) it by 10)
(5) – (4)
10000x – 1000x = (-212137.7777…) – (-21213.7777…)
9000x = -190924
x = –\(\frac { 190924 }{ 9000 }\)
9th Maths 2.2 Question 5.
Without actual division, find which of the following rational numbers have terminating decimal expansion.
(i) \(\frac { 7 }{ 128 }\)
(ii) \(\frac { 21 }{ 15 }\)
(iii) 4\(\frac { 9 }{ 35 }\)
(iv) \(\frac { 219 }{ 2200 }\)
Solution:
(i) \(\frac { 7 }{ 128 }\)
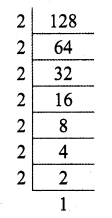
So \(\frac{7}{128}=\frac{7}{2^{7} 5^{0}}\)
This of the form 4m, n ∈ W
So \(\frac { 7 }{ 128 }\) has a terminating decimal expansion.
(ii) \(\frac { 21 }{ 15 }\)

So \(\frac { 21 }{ 15 }\) has a terminating decimal expansion.
(iii) 4\(\frac { 9 }{ 35 }\) = \(\frac { 149 }{ 35 }\)
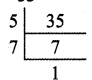
\(\frac{49}{35}=\frac{149}{5^{1} 7^{1}}\)
∴ This is not of the form \(\frac{p}{5^{1} 7^{1}}\)
So 4\(\frac { 9 }{ 35 }\) has a non-terminating recurring decimal expansion.
(iv) \(\frac { 219 }{ 2200 }\)

\(\frac{219}{2200}=\frac{219}{2^{3} 5^{2} 11^{1}}\)
∴ This is not of the form \(\frac{p}{2^{m} 5^{n}}\)
So \(\frac { 219 }{ 2200 }\) has a non-terminating recurring decimal expansion.