You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.5
Exercise 1.5 Class 9 Maths Samacheer Question 1.
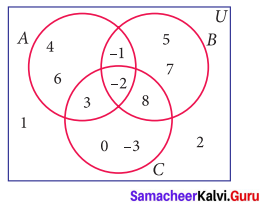
Using the adjacent venn diagram, find the following sets:
(i) A – B
(ii) B – C
(iii) A’ ∪ B’
(vi) A’ ∩ B’
(v) (B ∪ C)’
(vi) A – (B ∪ C)
(vii) A – (B ∩ C)
Solution:
(i) A – B = {3, 4, 6}
(ii) B – C = {-1, 5, 7}
(iii) A’ ∪ B’
A’ = {1, 2, 0, -3, 5, 7, 8}
B’ = {-3, 0, 1, 2, 3, 4, 6)
A’ ∪ B’ = {-3, 0, 1, 2, 3, 4, 5, 6, 7, 8)
(iv) A’ ∩ B’
A’ ∩ B’ = {-3, 0, 1, 2}
(v) B ∪ C = {-3, -2, -1, 0, 3, 5, 7, 8}
(B ∪ C)’ = U – (B ∪ C)
= {-3, -2, -1, 0, 1,2, 3, 4, 5, 6, 7, 8} – {-3, -2, -1, 0, 3, 5, 7, 8}
(B ∪ C)’ = {1, 2, 4, 6}
(vi) A – (B ∪ C) = {-2, -1, 3, 4,6} – {-3, -2, -1, 0, 3, 5, 7, 8} = {4, 6}
A – (B ∩ C)
B ∩ C = {-2, 8}
A- (B ∩ C) = {-2, -1, 3, 4, 6} – {-2, 8} = {-1, 3, 4, 6}
9th Maths Exercise 1.5 Samacheer Kalvi Question 2.
If K = {a, b, d, e,f}, L = {b, c, d, g} and M {a, b, c, d, h} then find the following:
(i) K ∪ (L ∩ M)
(ii) K ∩ (L ∪ M)
(iii) (K ∪ L) ∩ (K ∪ M)
(iv) (K ∩ L) ∪ (K ∩ M) and verify distributive laws.
Solution:
K = {a, b, d, e, f}, L = {b, c, d, g} and M {a, b, c, d, h}
(i) K ∪ (L ∩ M)
L ∩ M = {b, c, d, g} ∩ {a, b, c, d, h} = {b, c, d}
K ∪ (L ∩ M) = {a, b, d, e, f } ∪ {b, c, d) = {a, b, c, d, e, f}
(ii) K ∩(L ∪ M)
L ∪ M = {a, b, c, d, g, h}
K ∩ (L ∪ M) = {a, b, d, e, f} ∩ {a, b, c, d, g, h} = {a, b, d}
(iii) (K ∪ L) ∩ (K ∪ M)
K ∪ L = {a, b, c, d, e, f, g}
K ∪ M = {a, b, c, d, e, f, h}
(K ∪ L) ∩ (K ∪ M) = {a, b, c, d, e,f}
(iv) (K ∩ L) ∪ (K ∩ M)
(K ∩ L) = {b, d)
(K ∩ M) = {a,b,d}
(K ∩ L) ∪ (K ∩ M) = {b, d} ∪ {a, b, d} = {a, b, d}
Distributive laws
K ∪ (L ∩ M) = (K ∪ L) ∩ (K ∪ M)
{a, b, c, d, e, f) = {a, b, c, d, e, f, g} ∩ {a, b, c, d, e, f, h}
= {a, b, c, d, e, f}
Thus Verified.
K ∩ (L ∪ M) = (K ∩ L) ∪ (K ∩ M)
{a, b, d} = {a, b, c, d, e, f, g} ∪ {a, b, c, d, e, f, h}
= {a, b, d}
Thus Verified.
9th Maths Set Language Exercise 1.5 Question 3.
If A = {x : x ∈ Z, -2 < x ≤ 4}, B = {x : x ∈ W, x ≤ 5}, C ={-4, -1, 0, 2, 3, 4}, then verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Solution:
A = {x : x ∈ Z, -2 < x ≤ 4} = {-1, 0, 1, 2, 3, 4}
B = {x : x ∈ W, x ≤ 5} = {0, 1, 2, 3, 4, 5}
C = {-4, -1, 0, 2, 3, 4}
A ∪ (B ∩ C)
B ∩ C = {0, 1, 2, 3, 4, 5} ∩ {-4, -1, 0, 2, 3, 4} = {0, 2, 3, 4}
A ∪ (B ∩ C) = {-1, 0, 1, 2, 3, 4} ∪ (0, 2, 3, 4} ={-1, 0, 1, 2, 3, 4} …………. (1)
(A ∪ B) ∩ (A ∪ C)
A ∩ B = {0, 1, 2, 3, 4}
A ∩ C = {-1, 0, 2, 3, 4}
(A ∩ B) ∪ (A ∩ C) = {0, 1, 2, 3, 4} ∪ {-1, 0, 2, 3, 4}= {-1, 0, 1, 2, 3, 4} …………. (2)
From (1) and (2), it is verified that
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
9th Maths Exercise 1.5 Question 4.
Verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) using Venn diagrams.
Solution:
L.H.S A ∪ (B ∩ C)
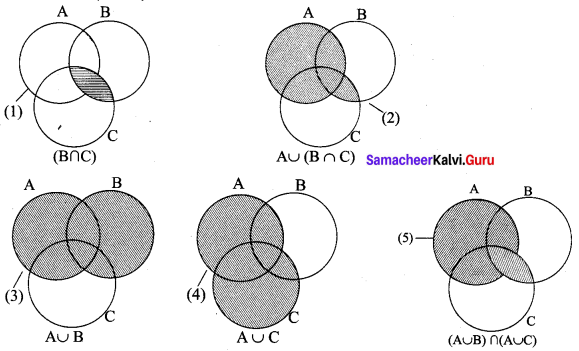
From (2) and (5), it is verified that A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Class 9 Maths Chapter 1 Samacheer Kalvi Question 5.
If A = {b, c, e, g, h}, B = {a, c, d, g, i} and C = {a, d, e, g, h}, then show that A – (B ∩ C) = (A – B) ∪ (A – C).
Solution:
A = {b, c, e, g, h}
B = {a, c, d, g, i}
C = {a, d, e, g, h}
B ∩ C = {a, d, g}
A – (B ∩ C) = {b, c, e, g, h} – {a, d, g} = {b, c, e, h} ……..… (1)
A- B = {b, c, e, g, h} – {a, c, d, g, i} = {b, e, h}
A – C = {b, c, e, g, h} – {a, d, e, g, h} = {b, c}
(A – B) ∪ (A – C) = {b, c, e, h} ………..… (2)
From (1) and (2) it is verified that
A – (B ∩ C) = (A – B) ∪ (A – C)
Samacheerkalvi.Guru 9th Maths Question 6.
If A = {x : x = 6 n ∈ W and n < 6}, B = {x : x = 2n, n ∈ N and 2 < n ≤ 9} and C = {x : x = 3n, n ∈ N and 4 ≤ n < 10}, then show that A – (B ∩ C) = (A – B) ∪ (A – C)
Solution:
A = {x : x = 6n, n ∈ W, n < 6}
x = 6n
n = {0, 1, 2, 3, 4, 5}
⇒ x = 6 × 0 = 0
x = 6 × 1= 6
x = 6 × 2 = 12
x = 6 × 3 = 18
x = 6 × 4 = 24
x = 6 × 5 = 30
∴ A = {0, 6, 12, 18, 24, 30}
B = { x : x = 2n, n ∈ N, 2 < n ≤ 9}
n = {3, 4, 5, 6, 7, 8, 9}
x = 2 n
⇒ x = 2 × 3 = 6
2 × 4 = 8
2 × 5 = 10
2 × 6 = 12
2 × 7 = 14
2 × 8 = 16
2 × 9 = 18
∴ B {6, 8, 10, 12, 14, 16, 18}
C = { x : x = 3n, n ∈ N, 4 ≤ n < 10}
N = { 4, 5, 6, 7, 8, 9}
x = 3 × 4 = 12
⇒ x = 3 × 5 = 15
x = 3 × 6 = 18
x = 3 × 7 = 21
x = 3 × 8 = 24
x = 3 × 9 = 27
x = 2 × 9 = 18
∴ C = {12, 15, 18, 21, 24, 27}
A – (B ∩ C) = (A – B) ∪ (A – C)
L.H.S R.H.S
B ∩ C = {12,18}
A – (B ∩ C) = {0, 6, 12, 18, 24, 30} – {12, 18} = {0, 6, 24, 30} ……….…. (1)
(A – B) = {0, 24, 30}
(A – C) = {0, 6, 30}
(A – B) ∪ (A – C) = {0, 6, 24, 30} …………. (2)
From (1) and (2), it is verified that
A – (B ∩ C) = (A – B) ∪ (A – C).
Samacheer Kalvi Guru 9th Maths Question 7.
If A = {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6} and C = {-1, 2, 5, 6, 7}, then show that A – (B ∪ C) = (A – B) ∩ (A – C).
Solution:
A = {-2, 0, 1, 3, 5},
B = {-1, 0, 2, 5, 6}
C ={-1, 2, 5, 6, 7}
B ∪ C = {-1, 0, 2, 5, 6, 7}
A – (B ∪ C) = {-2, 1, 3} …………. (1)
(A – B) = {-2, 1, 3}
(A – C) = {-2, 0, 1, 3}
(A – B) ∩ (A – C) = {-2, 1, 3} ………..… (2)
From (1) and (2), it is verified that . A – (B ∪ C) = (A – B) ∩ (A – C)
9th Standard Maths Exercise 1.5 Question 8.
if A={y: y = \(\frac{a+1}{2}\), a ∈ W and a ≤ 5},B = {y: y=\(\frac{2 n-1}{2}\),n ∈ W and n < 5} and C={−1,\(-\frac{1}{2}\), 1, \(\frac{3}{2}\), 2} then show that A – (B ∪ C) = (A – B) ∩ (A – C).
Solution:
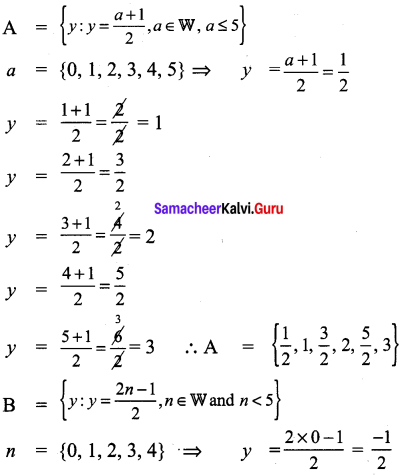
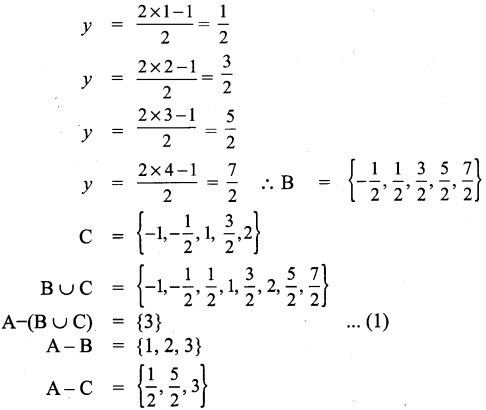
(A – B) ∩ (A – C) = {3} …………. (2)
From (1) and (2), it is verified that A – (B ∪ C) = (A – B) ∩ (A – C).
9th Maths Exercise 1.5 In Tamil Question 9.
Verify A – (B ∩ C) = (A – B) ∪ (A – C) using Venn diagrams.
Solution:
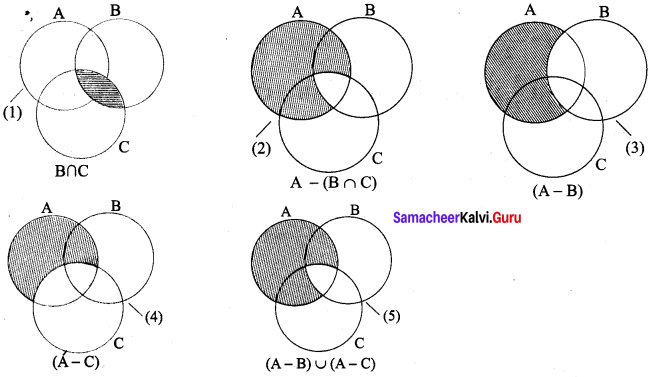
∴ A – (B ∩ C) = (A – B) ∪ (A – C)
Hence it is proved.
Kalvi Guru 9th Maths Question 10.
If U = {4, 7, 8, 10, 11, 12, 15, 16}, A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan’s Laws for complementation.
U = {4, 7, 8, 10, 11, 12, 15, 16}
A = {7, 8, 11, 12}, B = {4, 8, 12, 15}
De Morgan’s Laws for complementation.
(A ∪ B)’ = A’ ∩ B’
A ∪ B = {4, 7, 8, 11, 12, 15}
(A ∪ B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 7, 8, 11, 12, 15}
= {10, 16} ……………. (1)
A’ = {4, 10, 15, 16}
B’ = {7, 10, 11, 16}
A’ ∩ B’ = {10, 16} ………………(2)
From (1) and (2) it is verified that (A ∪ B)’ = A’ ∩ B’.
9th Class Math Exercise 1.5 Solution Question 11.
Verify (A ∩ B)’ = A’ ∪ B’ using Venn diagrams.
Solution:
(A ∩ B)’ = A’ ∪ B’
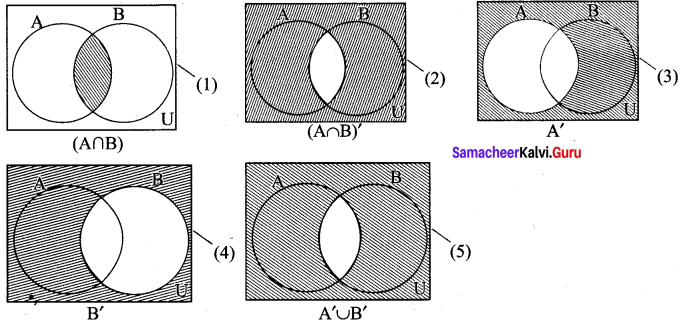
(2) = (5)
∴ (A ∩ B)’ = A’ ∪ B’