Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4

Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4

8th Standard Maths Exercise 3.4 Question 1.
Factorise the following by taking out the common factor
(i) 18xy – 12yz
(ii) 9x⁵y³ + 6x³y² – 18x²y
(iii) x(b – 2c) + y(b – 2c)
(iv) (ax + ay) + (bx + by)
(v) 2x²(4x – 1) – 4x + 1
(vi) 3y(x – 2)² – 2(2 – x)
(vii) 6xy – 4y² + 12xy – 2yzx
(viii) a³ – 3a² + a – 3
(ix) 3y³ – 48y
(x) ab² – bc² – ab + c²
Solution:
(i) 18xy – 12yz = (2 × 3 × 3 × y × x) – (2 × 2 × 3 × y × z)
Taking out the common factors 2, 3, y, we get
= 2 × 3 × y (3x – 2z) = 6y (3x- 2z)

i) 9x⁵y³ + 6x³y² – 18x²y = (3 × 3 × x² × x³ × y × y²) + (2 × 3 × x² × x × y × y)
Taking out the common factors 3, x², y, we get
= 3 × x² × y (3x³ y² + 2xy – 6)
= 3x²y (3x³ y² + 2xy – 6)

(iii) x(b – 2c) + y(b – 2c)
Taking out the binomial factor (b – 2c) from each term, we have
= (b – 2c)(x + y)

(iv) (ax + ay) + (bx + by)
Taking at ‘a’ from the first term and ‘b’ from the second term we have
(ax + ay) + (bx + by) = a (x + y) + b (x + y)
Now taking out the binomial factor (x + y) from each term
= (x + y)(a + b)

(v) 2x²(4x – 1) – 4x + 1
Taking out -1 from last two terms
2x² (4x – 1) – 4x + 1 = 2x² (4x – 1) – 1 (4x- 1)
Taking out the binomial factor 4x – 1, we get
= (4x – 1)(2x² – 1)

(vi) 3y(x – 2)² – 2(2 – x)
3y(x – 2)² – 2(2 – x) = 3y(x – 2)(x – 2)-2(-1) (x – 2) [∵ Taking out -1 from 2 – x]
= 3y (x – 2) (x – 2) + 2 (x – 2)
Taking out the binomial factor x – 2 from each term, we get
= (x – 2) [3y (x – 2) + 2]

(vii) 6xy – 4y² + 12xy – 2yzx
= 6xy + 12xy – 4y² – 2yzx [∵ Addition is commutative]
= (6 × x × y) + (2 × 6 × x × y) + (-1) (2) (2) y + y) + ((-1) (2) (y) (z) (x))
Taking out 6 × x × y from first two terms and (-1) × 2 × y from last two terms we get
= 6 × x × y(1 + 2) + (-1)(2)y[2y + zx]
= 6xy (3) -2y(2y + zx)
= (2 × 3 × 3 × x × y) – 2xy (2y + zx)
Taking out 2y from two terms
= 2y (9x – (2y + zx)) = 2y (9x – 2y – xz)

(viii) a² – 3a² + a – 3 = a² (a – 3) + 1 (a – 3) [∵ Grouping the terms suitably]
= (a – 3) (a² + 1)

(ix) 3y² – 48y = 3 × y × y² – 3 × 16 × y
Taking out 3 × y = 3y (y² – 16) = 3y (y² – 4²)
Comparing y² – 4² with a² – b²
a = y, b = 4
a² – b² = (a + b) (a – b)
y² – 4² = (y + 4) (y – 4)
∴ 3y (y² – 16) = 3y (y + 4) (y – 4)

(x) ab² – bc² – ab + c²
Grouping suitably
ab² – bc² – ab + c² = b ((ab – c²) – 1(ab – c²)
Taking out the binomial factor ab – c² = (ab – c²) (b – 1)

Samacheer Kalvi Guru 8th Maths Question 2.
Factorise the following expressions
(i) x² + 14x + 49
(ii) y² – 10y + 25
(iii) c² – 4c – 12
(iv) m² + m – 72
(v) 4x² – 8x + 3
Solution:
x² + 14x + 49 = x² + 14x + 72
Comparing with a² + 2ab + b² = (a + b)² we have a = x and b = 7
⇒ x² + 2(x) (7) + 7² = (x + 7)²
∴ x² + 14x + 49 = (x + 7)²

(ii) y² – 10y + 25 = y² – 10y + 5²
Comparing with a² – 2ab + b² = (a – b)² we get a = y ; b = 5
⇒ y² – 2(y) (5) + 5² = (y – 5)²
∴ y² – 10y + 25 = (y – 5)²

(iii) c² – 4c – 12
This is of the form ax² + bx + c
Where a = 1,b = – 4 c = – 12, x = c
Now the product ac = 1 × – 12 = – 12 and the sum b = -4

(iv) m² + m – 72

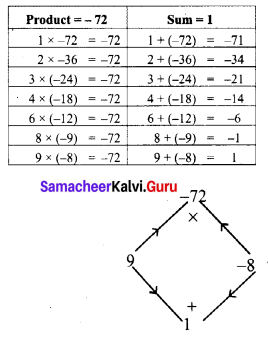
This is of the form ax² + bx + c
where a = 1, b = 1, c = -12
Product a × c = 1 × -72 = -72
Sum b = 1
The middle term m can be written as 9m – 8m
m² + m – 72 = m² + 9m – 8m – 12
= m (m + 9) – 8 (m + 9)
Taking out (m + 9)
= (m + 9) (m – 8)
∴ m² + m – 72 = (m + 9) (m – 8)

(v) 4x² – 8x + 3
This is of the form ax² + bx + c with a = 4 b = -8 c = 3
Product ac = 4 × 3 = 12
Sum b = -8

Samacheer Kalvi Guru Maths 8th Question 3.
Factorize the following expressions using a³ + b³ = (a + b)(a² – ab + b²) identity
(i) h³ + k²
(ii) 2a³ + 16
(iii) x³y³ + 27
(iv) 64m³ + n³
(v) r⁴ + 27p³r
Solution:
(i) h³ + k³
Comparing h³ + k³ with a³ + b³ = (a + b)(a² – ab + b²) we have a = h, b = k
∴ h³ + k³ = (h + k)(h² – hk + k²)

(ii) 2a² + 16
(2 × a³) + (2 × 8) = 2(a³ + 8) = 2 (a³ + 2³)
∴ 2a³ + 16 = 2 (a³ + 2³)
Comparing with a³ + b³ we have a = a and b = 2
a³ + b³ = (a + b)(a² – ab + b²)
2(a³ + 2³) = 2[(a + 2) (a² – (a) (2) + 2²)] = 2[(a + 2) (a² – 2a + 4)]
2a³ +16 = 2 (a + 2) (a² – 2a + 4)

(iii) x³ y³ + 27 = (xy)³ + 3³
Comparing with a³ + b³ we have a = xy ;b = 3
a³ + b³ = (a + b) (a² – ab + b²)
(xy)³ + 3³ = (xy + 3) ((xy)² – (xy) (3) + 3²) = (xy + 3) (x²y² – 3xy + 9)
∴ x³y³ + 27 = (xy + 3)(x²y² – 3xy + 9)

(iv) 64m³ + n³ = (4³m³) + n³
= (4m)³ + n³
Comparing this with a³ + b³ we have a = 4m; b = n
a³ + b³ = (a + b) (a² – ab + b²)
(4m)³ + n³ = (4m + n) [(4m)2 – (4m) (n) + n2]
= (4m + n) [4²m² – 4mn + n²]
= (4m + n) [ 16m² – 4mn + n²]
64m³ + n³ = (4m + n) (16m² – 4mn + n²)

(v) r³ + 27p³r = r (r³ + 27p³) = r [r³ + 3³p³]
Comparing r³ + (3p)³ with a³ + b³ we have a = r; b = 3p
a³ + b³ = (a + b)(a² – ab + b²)
r[r³ + (3p)³] = r[(r + 3p)(r² – r(3p) + (3p)²)]
= r[(r+ 3p) (r² – 3rp + 3²p²]
= r(r + 3p) (r² – 3rp + 9p²)
r⁴ + 27p³r = r(r + 3p) (r² – 3rp + 9p²)

11th Maths Exercise 3.4 Samacheer Kalvi Question 4.
Factorize the following expressions using a³ – b³ = (a – b)(a² + ab + b²) identity
(i) y³ – 27
(ii) 3b³ – 192c³
(iii) -16y³ + 2x³
(iv) x³ y³ – 7³
(v) c³ – 27b³ a³
Solution:
(i) y³ – 27 = y³ – 3³
Comparing this with a³ – b³ , we have a = y and b = 3
a³ – b³ = (a + b) (a² + ab + b² )
y³ – 3³ = (y – 3)(y² + (y) (3) + 3² ) = (y – 3) (y² + 3y + 9)
y³ – 27 = (y – 3) (y² + 3y + 9)

(ii) 3b³ + 192c³ = (3 × b³) – (3 × 4 × 4 × 4 × c³) = 3(b³ – 4³ c³)
= 3(b³ – (4c)³ )
Comparing b³ – (4c)³ with a³ – b³ we have a = b and b = 4c
a³ – b³ = (a – b) (a² + ab + b²)
3(b³ – (4c)³) = 3[(b – 4c)(b² + (b)(4c) + (4c)²)]
= 3[(b – 4c)(b² + 4bc + 4² c²)]
3b³ – 192c³ = 3 [(b – 4c) (b² + 4bc + 16c²)]

(iii) -16y³ + 2x³ = 2x³ – 16y³ [∵ Addition is commatative]
= 2(x³ – 8y³) = 2(x³ – 23y³)
= 2(x³ – (2y)³)
Comparing x³ – (2y)³ with a³ – b³ we have a = x and b = 2y
a³ – b³ = (a – b)(a² + ab + b²)
2[x³ – (2y)³] = 2[(x – 2y) (x² + (x) (2y) + (2y)²)]
= 2[(x – 2y) (x² + 2xy + 2² y²)]
-16y³ + 2x³ = 2[(x – 2y)(x² + 2xy + 4y²)]

(iv) x³y³ – 7³ = (xy)³ – 7³
Comparing with a³ – b³ we have a = xy and b = 7
a³ – b³ = (a – b)(a² + ab + b²)
(xy)³ – 7³ = (xy – 7) ((xy)² + (xy) (7) + 7²)
x³y³ – 7³ = (xy – 7) (x²y² + 7xy + 49)

(v) c³ – 27 b³ a³ = c³ – 3³b³ a³ = c³ – (3ba)³
Comparing this with a³ – b³ we have a = x and b = 3ba
a³ – b³ = (a – b)(a² + ab + b²)
∴ c³ – (3ba)³ = (c – 3ba) (c² + (c) (3ba) + (3ba)²)
= (c – 3ba) (c² + 3bac + 3² b²a²)
c³ – 27b³a³ = (c – 3ab) (c² + 3bac + 9a²b²)