Students can Download Maths Chapter 3 Geometry Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Ex 3.3
Question I.
Construct the following trapeziums with the given measures and also find their area.
Question 1.
AIMS with \(\overline { AI } \) ∥ \(\overline { SM } \), AI = 6 cm, IM = 5 cm, AM = 9 cm and MS 6.5 cm.
Solution:
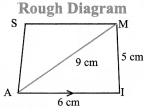
Given
AI = 6cm
IM = 5cm
AM = 9cm, and \(\overline { AI } \) ∥ \(\overline { SM } \)
MS = 6.5 cm
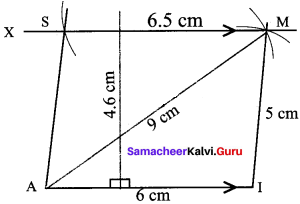
Construction:
Steps:
- Draw a line segment AI = 6cm.
- With A and I as centres, draw arcs of radii 9 cm and 5 cm respectively and let them cut at M
- Join AM and IM.
- Draw MX parallel to AI
- With M as centre, draw an arc of radius 6.5 cm cutting MX at S.
- Join AS AIMS is the required trapezium.
Calculation of Area:
Area of the trapezium AIMS = \(\frac{1}{2}\) x h x (a + b) sq.units
= \(\frac{1}{2}\) x 4.6 x (6 + 6.5) = \(\frac{1}{2}\) x 4.6 x 12.5
= 28.75 Sq.cm
![]()
Question 2.
BIKE with \(\overline { BI } \) ∥ \(\overline { EK } \), BI = 4 cm, IK = 3.5 cm, BK = 6 cm and BE = 3.5 cm
Solution:
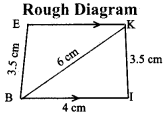
Given:
In the trapezium BIKE,
BI = 4 cm
IK = 3.5 cm
BK = 6 cm
BE = 3.5 cm and \(\overline { BI } \) ∥ \(\overline { EK } \)
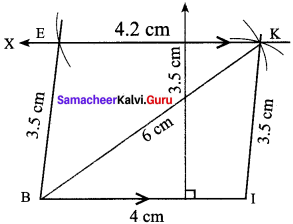
Construction:
Steps:
- Draw a line segment BI = 4 cm.
- With B and I as centres, draw arcs of radii 6 cm and 3.5 cm respectively and let them cut at K.
- Join BK and IK
- Draw KX parallel to BI
- With B as centre, draw an arc of radius 3.5 cm.cutting KX at E
- Join BE. BIKE is the required trapezium.
Calculation of area:
Area of the trapezium BIKE = \(\frac{1}{2}\) x h x (a + b) sq. units = \(\frac{1}{2}\) x 3.5 x (4 + 4.2)
= \(\frac{1}{2}\) x 3.5 x 8.2 = 14.35 sq.cm
Question 3.
CUTE with \(\overline { CD } \) ∥ \(\overline { ET } \), CU = 7 cm, ∠UCE = 80°, CE = 6 cm and TE = 5 cm.
Solution:
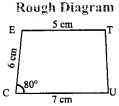
Given:
In the trapezium CUTE,
CU = 7 cm, ∠UCE = 80°,
CE = 6 cm, TE = 5 cm and \(\overline { CD } \) ∥ \(\overline { ET } \)
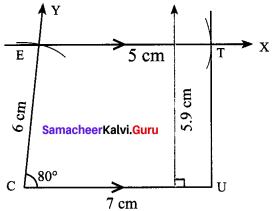
Construction:
Steps:
- Draw a line segment CU = 7 cm.
- Construct an angle ∠UCE = 80° at C
- With C as centre, draw an arc of radius 6 cm cutting CY at E
- Draw EX parallel to CU
- With E as centre, draw an arc of radius 5 cm cutting EX at T
- 6. Join UT. CUTE is the required trapezium.
Calculation of area:
Area of the trapezium CUTE = \(\frac{1}{2}\) x h x (a + b) sq. units = \(\frac{1}{2}\) x 5.9 x (7 + 5) sq. units
= 35.4 sq.cm –
Question 4.
DUTY with \(\overline { DU } \) ∥ \(\overline { YT } \), DU = 8 cm, ∠DUT = 60°, UT = 6 cm and TY = 5 cm.
Solution:
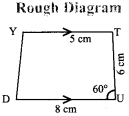
Given:
In the trapezium DUTY
DU = 8 cm, ∠DUT = 60°,
UT = 6 cm, TY = 5 cm and \(\overline { DU } \) ∥ \(\overline { YT } \)
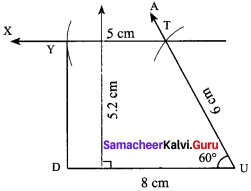
Construction:
Steps:
- Draw a line segment DU = 8 cm.
- Construct an angle ∠DUT = 60° at U
- With U as centre, draw an arc of radius 6 cm cutting UA at T.
- Draw TX parallel to DU
- With T as centre, draw an arc of radius 5 cm cutting TX at Y
- Join DE. DUTY is the required trapezium.
Calculation of area:
Area of the trapezium DUT Y = \(\frac{1}{2}\) x h x (a + b) sq. units= \(\frac{1}{2}\) x 5.2 x (8 + 5) sq. units = \(\frac{1}{2}\) x 5.2 x 13
= 33.8 sq.cm ,
![]()
Question 5.
ARMY with \(\overline { AR } \) ∥ \(\overline { YM } \), AR = 7 cm, RM = 6.5 cm ∠RAY = 100° and ∠ARM = 60° 5
Solution:
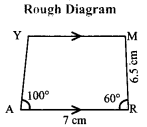
Given:
In the trapezium ARMY
AR = 7 cm, RM = 6.5 cm,
∠RAY = 100° and ARM = 60°, \(\overline { AR } \) ∥ \(\overline { YM } \)
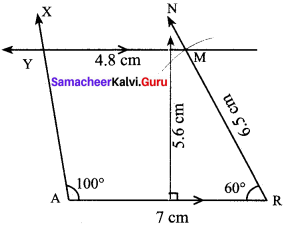
Construction:
Steps:
- Draw a line segment AR = 7 cm.
- Construct an angle ∠RAX = 100° at A
- Construct an angle ∠ARN = 60° at R
- With R as centre, draw an arc of radius 6.5 cm cutting RN at M
- Draw MY parallel to AR
- ARMY is the required trapezium.
Calculation of area:
Area of the trapezium ARMY = \(\frac{1}{2}\) x h x (a + b) sq. units = \(\frac{1}{2}\) x 5.6 x (7 + 4.8) sq. units
= \(\frac{1}{2}\) x 5.6 x 11.8 = 33.04 sq.cm
Question 6.
BELT with \(\overline { BE } \) ∥ \(\overline { TL } \), BT = 7 cm ∠EBT = 85° and ∠BEL = 110°
Solution:
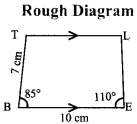
Given:
In the trapezium BELT
BE = 10 cm, BT = 7cm,
∠EBT = 85°, ∠BEL = 110° and \(\overline { BE } \) ∥ \(\overline { TL } \)
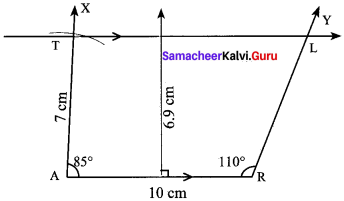
Construction:
Steps:
- Draw a line segment BE = 10 cm.
- Construct two angles ∠TBE = 85° and ∠BEL =110° respectively at the points B and E.
- With B as centre, draw an arc of radius 7 cm cutting BX at T.
- Draw TL ∥ BE
- BELT is the required trapezium
Question 7.
CITY with \(\overline { CI } \) ∥ \(\overline { YT } \) Cl = 7 cm, IT = 5.5 cm, TY = 4 cm and YC = 6 cm.
Solution:
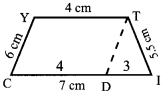
Given:
In the trapezium CITY,
Cl = 7 cm
IT = 5.5 cm
TY = 4 cm
YC = 6 cm, and \(\overline { CI } \) ∥ \(\overline { YT } \)
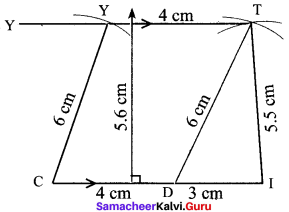
Construction:
Steps:
- Draw a line segment Cl = 7 cm.
- Mark a point D on Cl such that CD = 4cm
- With D and I as centres, draw arcs of radii 6 cm and 5.5 cm respectively. Let them cut at T. Join DT and IT.
- With C as centre, draw an arc of radius 6 cm.
- Draw TY parallel to CL Let the line cut the previous arc at Y.
- Join CY. CITY is the required trapezium.
Calculation of area:
Area of the trapezium CITY = \(\frac{1}{2}\) x h x (a + b) sq. units
= \(\frac{1}{2}\) x 5.5 x (7 + 4) sq. units = \(\frac{1}{2}\) x 5.5 x 11
= 30.25 sq.cm
![]()
Question 8.
DICE with \(\overline { DI } \) ∥ \(\overline { EC } \), DI = 6 cm, IC = ED = 5 cm and CE = 3 cm. Solution:
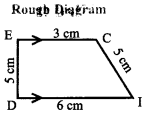
Given:
In the trapezium DICE,
DI = 6 cm
IC = ED = 5 cm
CE = 3 cm and \(\overline { DI } \) ∥ \(\overline { EC } \)
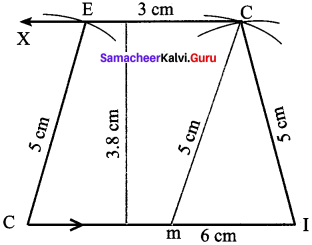
Construction:
Steps:
- Draw a line segment DI = 6 cm.
- Mark a point M on DI such that DM = 3cm
- With D and I as centres, draw arcs of radii 5 cm each Let them cut at C. Join MC and IC.
- Draw CX parallel to DI
- With D as centre, draw an arc of radius 5 cm. Let it cut CX at E
- Join DE. DICE is the required trapezium.
Calculation of area:
Area of the trapezium DICE = \(\frac{1}{2}\) x h x (a + b) sq. units = \(\frac{1}{2}\) x 3.8 x (6 + 3) sq. units
= \(\frac{1}{2}\) x 3.8 x 9 = 17.1 sq. cm