Students can Download Maths Chapter 1 Life Mathematics Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 1 Life Mathematics Intext Questions
Exercise 1.1
Try This (Text book Page no. 1)
Question 1.
Find the indicated percentage value of the given numbers
Solution:

Think (Text book page no. 6)
Question 1.
An increase from 200 to 600 ¡s clearly a 200%increase. Isn’t it? (check!). With a lot of pride, the traffic police commiuêener of a city reported that the accidents had decreased by 200% ¡n one year. He cameupwith this number stating that the accidents had gone down from 600 last year to 2this year. Is the decrease from 600 to 200, the same 200% as above? Justify.
Solution:
Increase from original value 200 to 600
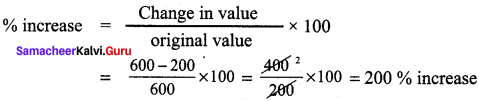
Decrease from original value 600 to 200
![]()
here original value is 600
% decrease = \(\frac{600-200}{600}\) x 100 = \(\frac{400}{600}\) x 100 = 66.67% decrease
Increase from 200 → 600 and % decrease from 600 → 200 are not the same
Try This (Text book page no. 7)
Question 1.
What percent of a day is 10 hours?
Solution:
In a day, there are 24 hours
10 hrs out of 24 hrs is \(\frac{10}{24}\)
As a percentage, we need to multiply by 100
∴ Percentage = \(\frac{10}{24}\) x 100 = 41.67%
![]()
Question 2.
Divide ₹ 350 among P, Q and R such that P gets 50% of what Q gets and Q gets 50% of what R gets.
Solution:
Let R get x, Q gets 50% of what R gets
∴ Q gets = \(\frac{50}{100}\) × x = \(\frac{x}{2}\)
P gets 50% of what Q gets
∴ P gets = \(\frac{50}{100}\) x \(\frac{x}{2}\) = \(\frac{x}{4}\)
Since 350 is divided among the three
∴ 350 = x + \(\frac{x}{2}\) + \(\frac{x}{4}\)
350 = \(\frac{4x+2x+x}{4}\) = \(\frac{7x}{4}\) = 350
x = \(\frac{350×4}{7}\) = 200
Q gets = \(\frac{x}{2}\) = \(\frac{200}{2}\) = 100,
P gets = \(\frac{x}{4}\) = \(\frac{200}{4}\) = 50
∴ P = 50
Q = 100
R = 200
Exercise 1.2
Think (Text book Page No. 13)
Question 1.
A shopkeeper marks the price of a marker board 15% above the cost price and then allows a discount of 15% on the marked price. Does he gain or lose in the transaction?
Solution:
Let cost price of marker board be 100
CP = 100 Marks it 15% above CP
∴ Marked price = MP = \(\frac{15}{100}\) x CP + CP = \(\frac{15}{100}\) 100 + 100 = 15 + 100 = 115
Discount % = 15%
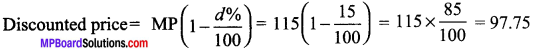
∴ He sells it 97.75 which is less than his cost price. Therefore he loses
Loss = 97.75 – 100 = – 2.25
Try This (Text book Page No. 14)
Question 1.
By selling 5 articles, a man gains the cost price of 1 article. Find his gain percentage.
Solution:
Let cost price of article be C.P. Let S.P of 1 articles be SP by selling 5 articles at SP he makes a gain of cost price of one article.
Gain on 1 article = SP – CP; ⇒ Gain% = \(\frac{SP-CP}{CP}\) x 100
Gain on 2 articles = 2 x (SP – CP)
Gain on 5 articles = 5 x (SP – CP)
Given than gain on 5 articles is CP of 1 article
∴ 5(SP – CP) = CP
\(\frac{SP-CP}{CP}\) = \(\frac{1}{5}\)
Gain percentage \(\frac{SP-CP}{CP}\) x 100 = \(\frac{1}{5}\) x 100 % = 20%
![]()
Question 2.
By selling 8 articles, a shopkeeper gains the selling price of 3 articles. Find his gain percentage.
Solution:
Let cost price of 1 article be CP. Let selling price of 1 article be SP.
Gain on 1 article = SP – CP
Gain on 8 articles = 8 x (SP – CP)
Given that gain on 8 articles in selling price of 3 articles
8(SP – CP) = 3 x SP
∴ \(\frac{SP-CP}{CP}\) = \(\frac{3}{8}\)
∴ \(\frac{SP}{SP-CP}\) = \(\frac{8}{3}\)
Subtracting 1 on both sides
\(\frac{SP}{SP-CP}\) – 1 = \(\frac{8}{3}\) – 1 = \(\frac{SP-(SP-CP)}{SP-CP}\)= \(\frac{8-3}{3}\)
\(\frac{SP-SP-CP}{SP-CP}\) = \(\frac{5}{3}\) ⇒ \(\frac{CP}{SP-CP}\) = \(\frac{5}{3}\)
\(\frac{SP-CP}{CP}\) = \(\frac{3}{5}\) (taking reciprocals on both sides)
Gain% \(\frac{SP-CP}{CP}\) x 100 = \(\frac{3}{5}\) x 100 = 3 x 20 = 60%
Question 3.
If the C.P of 20 articles is equal to the S.P of 15 articles, find the profit or loss percentage.
Solution:
Given CP of 20 article = SP of 15 articles
∴ SP of 15 articles = CP of 20 articles
∴ SP of 1 article = \(\frac{1}{15}\) x CP of 20 articles
SP = \(\frac{1}{15}\) x 20 CP = \(\frac{20}{15}\) CP = \(\frac{4}{3}\) CP
∴ SP = \(\frac{4}{3}\) CP ⇒ SP is greater than CP
It is a profit.

Exercise 1.3
Try This (Text book Page No. 23)
![]()
Question 1.
Find the principal which gives ₹ 420 as C.I @ 20% p.a compounded half yearly for one year.
Solution:
CI = ₹420
Rate = ₹ 20% p.a
Principle = ₹ [required to find] Time period (n) = 1 year.
However, let us value of r to be 20% p.a so for half yearly, r is \(\frac{20}{2}\) = 10%
Formula for Amount (A) when compounded half yearly is

Question 2.
The price of a laptop depreciates @ 4% p.a. If its present price is ₹ 24,000, find its price after 3 years.
Solution:
Let original price of laptop be ‘P’, Rate of depreciation is 4% p.a,
Present price is ₹ 24,000 (D).
Formula for depreciation is

Price after 3 years from now is
P(1 – \(\frac{4}{100}\))n+3 = ? ⇒ (1 – \(\frac{4}{100}\))n (1 – \(\frac{4}{100}\))3
From (1)
24,000 x (1 – \(\frac{4}{100}\))3
24,000 x \(\frac{96}{100}\) x \(\frac{96}{100}\) x \(\frac{96}{100}\) = 21233.66
Actvity I (text book Page No. 23)
Question 1.
Mukunthan invests 30,000/- for 3 months in a bank which gives C.I at the rate of 12% compounded monthly. A private company offers his S.l at the rate of 12% p.a What is the difference in the interests received by Mukunthan? Do by traditional method and verify your answer by calculator.
Solution:
Principal = 30,000
Time period = 3 months
In Bank rate of interest for CI = 12% compounded monthly
∴ A = (1 + \(\frac{r}{100}\))n = 30,000(1 + \(\frac{12}{100}\))3
30,000 x \(\frac{112}{100}\) x \(\frac{112}{100}\) x \(\frac{112}{100}\) = 42147.84
∴ CI = A – P = 42147.84 – 30,000
CI = 12147.84
In private company,
Rate of single Interest SI = 12% p.a
So, for 3 months, i.e \(\frac{3}{12}\) = \(\frac{1}{4}\) year,
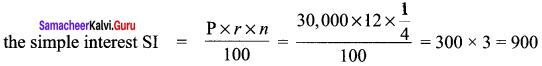
∴ Difference in interest = CI – SI = 12,147.84 – 900 = 11247.84
Read More: BHARTIARTL Pivot Calculator