Samacheer Kalvi 8th Maths Guide Chapter 2 அளவைகள் Ex 2.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 அளவைகள் Ex 2.1 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 2 அளவைகள் Ex 2.1

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக :

(i) வட்டத்தின் பரிதிக்கும் அதன் விட்டத்திற்கும் இடையேயான விகிதம் …………………
(ii) ஒரு வட்டத்தின் மீதுள்ள ஏதேனும் இரண்டு புள்ளிகளை இணைக்கும் கோடு …………………
(iii) ஒரு வட்டத்தின் மிகப்பெரிய நாண் …………………ஆகும்.
(iv) 24செ.மீ விட்ட அளவுள்ள ஒரு வட்டத்தின் ஆரம் …………………
(v) வட்டப்பரிதியின் ஒரு பகுதியே ………………… ஆகும்.
தீர்வு :
(i) π
(ii) நாண்
(iii) விட்டம்
(iv) 12செ.மீ
(v) வட்டவில்

கேள்வி 2.
பின்வருவனவற்றைப் பொருத்துக :
(i) வட்டத்தின் பரப்பளவு – அ) \(\frac{1}{4} \pi r^{2}\)
(ii) வட்டத்தின் சுற்றளவு – ஆ) (π + 2)r

(iii) வட்டக்கோணப் பகுதியின் பரப்பளவு – இ) πr²
(iv) அரைவட்டத்தின் சுற்றளவு – ஈ) 2πr
(v) கால்வட்டத்தின் பரப்பளவு – உ) \(\frac{\theta^{\circ}}{360^{\circ}} \times \pi r^{2}\)
விடை :
(i) இ) πr²
(ii) ஈ) 2πr
(i) உ) \(\frac{\theta^{\circ}}{360^{\circ}} \times \pi r^{2}\)
(iv) ஆ) (π + 2)r
(v) அ) \(\frac{1}{4} \pi r^{2}\)

கேள்வி 3.
நிழலிடப்பட்டுள்ள வட்டக்கோணப் பகுதிகளின் மையக்கோணங்களைக் காண்க. (ஒவ்வொரு வட்டமும் சம அளவு வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்பட்டுள்ளன).
im
தீர்வு :
(i) மையக்கோணம் = \(\frac{360^{\circ}}{n}=\frac{360^{\circ}}{2}=180^{\circ}\)
(ii) மையக் கோணம் = \(\frac{360^{0}}{n}=\frac{360^{\circ}}{5}=72^{0}\)
(iii) மையக்கோணம் = \(\frac{360^{\circ}}{n}=\frac{360^{\circ}}{8}=45^{0}\)
(iv) மையக்கோணம் = \(\frac{360^{0}}{n}=\frac{360^{0}}{10}=36^{0}\)

கேள்வி 4.
கீழே கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்ட வட்டக்கோணப் பகுதிகளின் வில்லின் நீளம், பரப்பளவு மற்றும் சுற்றளவு ஆகியவற்றைக் காண்க. (π = 3.14).
(i) மையக்கோணம் 45°, r = 16 செ.மீ.
(ii) மையக்கோணம் 120°,d= 12.6 செ.மீ
தீர்வு :
(i) θ = 45°, r = 16 செ.மீ
I = \(\frac{\theta^{\circ}}{360^{\circ}} \times 2 \pi \mathrm{r}\)அலகுகள்
= \(\frac{45}{360} \times 2 \times 3.14 \times 16^{2}\)
= 4 x 3.14
l = 12.56 செ.மீ.)
A = \(\frac{\theta^{\circ}}{360^{\circ}}\) x πr² ச.அ
= \(\frac{45}{360} \times 3.14 \times 16 \times 16^{2}\)
= 32 x 3.14
A = 100.48 செ.மீ²
p = 1 + 2r அலகுகள்
= 12.56 + 2 x 16
= 12.56 + 32
p = 44.56 செ.மீ

(ii) θ =120°, d = 12.6 செ.மீ
r = 6.3 செ.மீ.

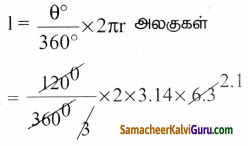
= 2 x 3.14 x 2.1
l = 13.19 செ.மீ

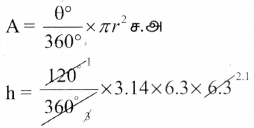
= 3.14 x 2.1 x 6.3
A = 41.54 ச செ.மீ
p = l + 2r அ
= 13.19 + 2 (6.3)
= 13.19+ 12.6
P = 25.79 செ.மீ

கேள்வி 5.
கீழே கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்ட வட்டக்கோணப் பகுதிகளின் பரப்பளவு காண்க.
(i) வட்ட வில்லின் நீளம் = 48மீ, r = 10மீ
(ii) வட்ட வில்லின் நீளம் = 50செ.மீ, r= 13.5செ.மீ
தீர்வு :
(i) l = 48e, r = 10மீ.
பரப்பு = \(\frac{l r}{2}\) ச.அ.
\(\frac{48 \times 10}{2}\)
A = 240 மீ²

(ii) l = 50 செ.மீ, r = 13.5 செ.மீ
பரப்பு = \(\frac{l r}{2}\) ச.அ.
\(\frac{50 \times 13.5}{2}\)
A= 337.5 செ.மீ²

கேள்வி 6.
கீழே கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்ட வட்டக்கோண பகுதிகளின் மையக்கோணம் காண்க. π = \(\frac{22}{7}\)
(i) பரப்பளவு = 462 செ.மீ r= 21 செ.மீ
(ii) வட்ட வில்லின் நீளம் = 44மீ, r = 35 மீ
தீர்வு :
(i) A = 462 செ.மீ² , r = 21 செ.மீ
பரப்பு = \(\frac{l r}{2}\) ச.அ.

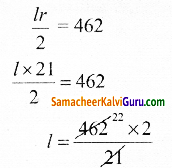
l = 44 செ.மீ

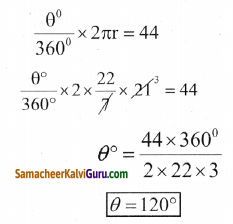
(ii) l = 44t, r = 35மீ
A = \(\frac{l r}{2}\) ச.அ
= \(\frac{44 \times 35}{2}\)
A = 770 செ.மீ²

கேள்வி 7.
(i) 120மீ ஆரமுள்ள வட்டமானது 8 சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்படுகிறது. அவை ஒவ்வொன்றின் வில்லின் நீளத்தையும் காண்க.
தீர்வு :
r = 120மீ, n = 8
வில்லின் நீளம் = \(\frac{1}{n}\) x 2πr அ.
= \(\frac{1}{8}\) x 2 x 1 x 120
l = 30π மீ.

கேள்வி 8.
70 செ.மீ ஆரமுள்ள வட்டமானது 5 சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்படுகிறது. அவை ஒவ்வொன்றின் பரப்பளவைக் காண்க.
தீர்வு :
(ii) r = 70 செ.மீ, n = 5.
பரப்பு = \(\frac{1}{n}\) x 2πr² ச.அ
= \(\frac{1}{5}\) x π x 70 x 70
A = 980π ச.செ.மீ (அ)
A = 980 x 22/7
A = 3080 செ.மீ²

கேள்வி 9.
தாமு தனது வீட்டின் தரைப்பகுதியில் 30 செ.மீ பக்க அளவுள்ள சதுரவடிவ ஒட்டினைப் பதித்துள்ளார். அந்த ஒடானது படத்தில் உள்ளவாறு வடிவமைப்பைப் பெற்றுள்ளது எனில், அதிலுள்ள வட்டக்கோணப் பகுதியின் பரப்பளவைக் காண்க . ( π = 3.14)
தீர்வு :
சதுரத்தின் பக்கம் = 30 செ.மீ
ஆரம் r= 30 செ.மீ, 0° = 90°

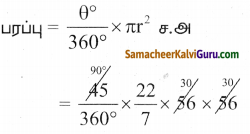
= 225 x 3.14
A = 706.5 செ.மீ²