Students can Download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 3 Algebra Ex 3.3
Miscellaneous Practice problems
Question 1.
Using identity, find the value of
(i) (4.9)2
(ii) (100.1)2
(iii) (1.9) × (2.1)
Solution:
(i) (4.9)2
(4.9)2 = (5 – 0.1)2
Substituting a = 5 and b = 0.1 in
(a – b)2 = a2 – 2ab + b2, we have
(5 – 0.1)2 = 52 – 2(5) (0.1) + (0.1)2
(4.9)2 = 25 – 1 + 0.01 = 24 + 0.01
(4.9)2 = 24.01
(ii) (100.1)2
(100.1)2 = (100 + 0.1)2
Substituting a = 100 and b = 0.1 in
(a + b)2 = a2 + 2ab + b2, we have
(100 + 0.1)2 = (100)2 + 2(100) (0.1) + (0.1)2
(100.1)2 = 10000 + 20 + 0.01
(100.1)2 = 10020.01
![]()
(iii) (1.9) × (2.1)
(1.9) × (2.1) = (2 – 0.1) × (2 + 0.1)
Substituting a = 100 and b = 0.1 in
(a – b) (a + b) = a2 – b2 we have
(2 – 0.1) (2 + 0.1) = 22 – (0.1)2
(1.9) × (2.1) = 4 – 0.01
(9.9) (2.1) = 3.99
Question 2.
Factorise: 4x2 – 9y2
Solution:
4x2 – 9y2 = 22 x2 – 32 y2 = (2x)2 – (3y)2
Substituting a = 2x and b = 3y in
(a2 – b2) = (a + b) (a – b), we have
(2x)2 – (3y)2 = (2x + 3y) (2x – 3y)
∴ Factors of 4x2 – 9y2 are (2x + 3y) and (2x – 3y)
Question 3.
Simplify using identities
(i) (3p + q) (3p + r)
(ii) (3p + q) (3p – q)
Solution:
(i) (3p + q) (3p + r)
Substitute x = 3p,a = q and b = r in
(x + a) (x + b) = x2 + x(a + b) + ab
(3p + q)(3p + r) = (3p)2 + 3p (q + r) + (q × r)
= 32 p2 + 3p (q + r) + qr
(3p + q)(3p + r) = 9p2 + 3p(q + r) + qr
(ii) (3p + q) (3p – q)
Substitute a = 3p and b = q in
(a + b) (a – b) = a2 – b2, we have
(3p + q) (3p – q) = (3p)2 – q2 = 32 p2 – q2
(3P + q) (3p – q) = 9p2 – q2
![]()
Question 4.
Show that (x + 2y)2 – (x – 2y)2 = 8xy.
Solution:
LHS = (x + 2y)2 – (x – 2y)2
= x2 + (2 × x × 2y) + (2y)2 – [x2 – (2 × x × 2y) + (2y)2]
= x2 + 4xy + 4y2 – [x2 – 4xy + 22y2]
= x2 + 4xy + 4y2 – x2 + 4xy – 4y2
= x2 – x2 + 4xy + 4xy + 4y2 – 4y2
= x2 (1 – 1) + xy (4 + 4) + y2 (4 – 4)
= 0x2 + 8xy + 0y2 = 8xy = RHS
∴ (x + 2y)2 – (x – 2y)2 = 8xy
[∵ (a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2]
Question 5
The pathway of a square paddy field has 5 m width and length of its side is 40 m. Find the total area of its pathway. (Note: Use suitable identity)
Solution:
Given side of the square = 40 m
Also width of the pathway = 5 m
∴ Side of the larger square = 40m + 2(5)m = 40m + 10m = 50m
Area of the path way = area of large square – area of smaller square
= 502 – 402
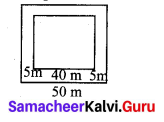
Substituting a = 50 and b = 40 in
a2 – b2 = (a + b) (a – b) we have
502 – 402 = (50 + 40) (50 – 40)
Area of pathway = 90 × 10
Area of the pathway = 900 m2
![]()
Challenge Problems
Question 1.
If X = a2 – 1 and Y = 1 – b2, then find X + Y and factorize the same.
Solution:
Given X = a2 – 1
Y = I – b2
X + Y = (a2 – 1) + (1 – b2)
= a2 – 1 + 1 – b2
We know the identity that a2 – b2 = (a + b) (a – b)
∴ X + Y = (a + b) (a – b)
Question 2.
Find the value of (x – y) (x + y) (x2 + y2).
Solution:
We know that (a – b) (a + b) = a2 – b2
Put a = x and b = y in the identity (1) then
(x – y) (x + y) = x2 – y2
Now (x – y) (x + y)(x2 + y2) = (x2 – y2) (x2 + y2)
Again put a = x2 and b = y2 in (1)
We have (x2 – y2) (x2 + y2) = (x2)2 – (y2)2 = x4 – y4
So (x – y) (x + y) (x2 + y2) = x4 – y4
![]()
Question 3.
Simplify (5x – 3y)2 – (5x + 3y)2.
Solution:
We have the identities
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
So (5x – 3y)2 – (5x + 3y)2 = (5x)2 – (2 × 5x × 3y) + (3y)2
= 52x2 – 30xy + 32 y2 – [52x2 – 30xy + 32 y2]
= 25x2 – 30xy + 9y2 – [25x2 + 30xy + 9y2]
= 25x2 – 30xy + 9y2 – 25x2 – 30xy – 9y2
= x2 (25 – 25) – xy (30 + 30) + y2 (9 – 9)
= 0x2 – 60xy + 0y2 = – 60 xy
∴ (5x – 3y)2 – (5x + 3y)2 = -60xy
Question 4.
Simplify : (i) (a + b)2 – (a – b)2
(ii) (a + b)2 + (a – b)2
Solution:
Applying the identities
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(i) (a + b)2 – (a – b)2 = a2 + 2ab + b2 – [a2 – 2ab + b2]
= a2 + 2ab + b2 – a2 + 2ab – b2
= a2 (1 – 1) + ab (2 + 2) + b2 (1 – 1)
= 0a2 + 4 ab + 0b2 = 4ab
(a + b)2 – (a – b)2 = 4ab
(ii) (a + b)2 + (a – b)2 = a2 + 2ab + b2 + (a2 – 2ab + b2)
= a2 + 2ab + b2 + a2 – 2ab + b2
= a2 (1 + 1) + ab (2 – 2) + b2 (1 + 1)
= 2a2 + 0 ab + 2b2 = 2a2 + 2b2 = 2 (a2 + b2)
∴ (a + b)2 – (a – b)2 = 2 (a2 + b2)
![]()
Question 5.
A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 m2, find the area of lawn.
Solution:
Let the side of the lawn = a m
then side Of big square = (a + 2(2)) m
= (a + 4)m
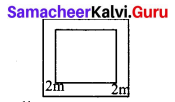
Area of the path – Area Of large square – Area of smaller square
136 = (a + 4)2 – a2
136 = a2 + (2 × a × 4) + 42 – a2
136 = a2 + 8a + 16 – a2
136 = 8a + 16
136 = 8 (a + 2)
Dividing by 8
17 = a + 2
Subtracting 2 on both sides
17 – 3 = a + 2 – 2
15 = a
∴ side of small square = 15 m
Area of square = (side × side) Sq. units
∴ Area of the lawn = (15 × 15)m2 = 225 m2
∴ Area of the lawn = 225 m2
![]()
Question 6.
Solve the following inequalities.
(i) 4n + 7 > 3n + 10, n is an integer
(ii) 6(x + 6) > 5 (x – 3), x is a whole number.
(iii) -13 < 5x + 2 < 32, x is an integer.
Solution:
(i) 4n + 7 > 3n + 10, n is an integer.
4n + 7 – 3n > 3n + 10 – 3n
n(4 – 3) + 7 > 3n + 10 – 3n
n (4 – 3) + 7 > n (3 – 3) + 10
n + 7 > 10
Subtracting 7 on both sides
n + 7 – 7 > 10 – 7
n > 3
Since the solution is an integer and is greater than or equal to 3, the solution will be 3,
4, 5, 6, 7, …..
n = 3, 4, 5, 6,7, ….
(ii) 6 (x + 6) > 5 (x – 3), x is a whole number.
6x + 36 > 5x – 15
Subtracting 5x on both sides
6x + 36 – 5x > 5x – 15 – 5x
x (6 – 5) + 36 > x(5 – 5) – 15
x + 36 > -15
Subtracting 36 on both sides
x + 36 – 36 > -15 -36
x > -51
The solution is a whole number and which is greater than or equal to -51
∴ The solution is 0, 1, 2, 3, 4,…
x = 0,1,2, 3,4,…
![]()
(iii) -13 < 5x + 2 < 32, x is an integer.
Subtracting throughout by 2
-13 – 2 < 5x + 2 – 2 < 32 – 2
-15 < 5x < 30
Dividing throughout by 5
\(\frac { -15 }{ 5 } \) < \(\frac { 5x }{ 5 } \) < \(\frac { 30 }{ 5 } \)
– 3 < x < 6
∴ Since the solution is an integer between -3 and 6 both inclusive, we have the solution
as -3, -2, -1,0, 1,2, 3, 4, 5, 6.
i.e. x = -3, -2, 0, 1, 2, 3,4, 5 and 6.