Students can Download English Poem 1 The Computer Swallowed Grandma Questions and Answers, Summary, Notes Pdf, Activity, Samacheer Kalvi 7th English Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th English Solutions Term 1 Poem Chapter 1 The Computer Swallowed Grandma
B. Read these lines and answer the questions given below.
The Computer Swallowed Grandma Poem Questions And Answers Question 1.
The computer swallowed grandma.
Answer:
Who swallowed Whom?
The computer swallowed grandma.
The Computer Swallowed Grandma Poem Question 2.
She pressed ‘Control’ and ‘Enter’
And disappeared from view.
How did Grandma disappear from view?
Answer:
Grandma disappeared from the view on the computer screen when she pressed the control’ and enter’ keys.
The Computer Swallowed Grandma Question 3.
It devoured her completely.
Who does ’if refer to?
Answer:
‘It’ refers to the computer.
The Computer Swallowed Grandma Poem Summary Question 4.
She must have caught a virus Or been eaten by a worm.
What happened to Grandma?
Answer:
Grandma was affected by computer ‘virus’.
The Computer Swallowed Grandma Poem Answers Question 5.
I’ve searched through the recycle bin And files of every kind;
I’ve even used the Internet,
But nothing did I find.
Where did the author search for grandma?
Answer:
The author searched Grandma in the recycle bin, files and on the internet.
C. Work in pairs. Read the last two stanzas of the poem and answer the following questions.
The Computer Swallowed Grandma Poem Paragraph Question 1.
Who did the author ask for grandma?
Answer:
The author asked Jeeves.
Computer Swallowed Grandma Poem Question 2.
Did the author get a positive reply?
Answer:
No, the author did not get a positive reply.
The Computer Swallowed Grandma Poem Book Back Answers Question 3.
What is the author’s plea?
Answer:
The author pleads to send grandma back to him by an email, if anyone sees her in their Inbox
D. Pick out the rhyming pairs and write them in the blanks given.
Answer:

The Computer Swallowed Grandma Additional Questions
Poem Comprehension – Additional
7th English Poem The Computer Swallowed Grandma Question 1.
In desperation, I asked Jeeves
My searches to refine.
The reply from him was negative,
Not a thing was found Online’.
(a) Why was the poet desperate?
Answer:
The poet was desperate as her old Grandmother had disappeared.
(b) Who was Jeeves?
Answer:
Jeeves was a software engineer called to repair the computer to bring back Grandma.
(c) Did Jeeves spot Grandma?
Answer:
No, he could not find Grandma.
(d) What do you understand from the last line?
Answer:
Not only Grandma, nothing was found ‘online’. That means the computer was not connected to the internet.
I. One Word Two Meanings.
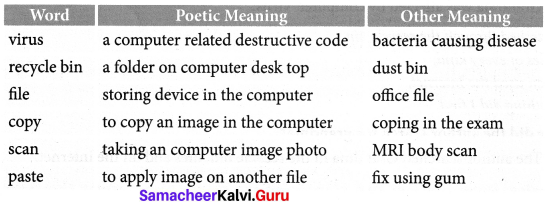
II. Short Questions and Answers.
7th Standard English The Computer Swallowed Grandma Question 1.
List the computer terms used in the poem.
Answer:
Control, enter, virus, recycle bin, files, internet, online, inbox, copy, scan, paste.
The Computer Swallowed Grandma Poem Summary In Tamil Question 2.
Did Grandma really got swallowed by the computer?
Answer:
No, Grandma did not get swallowed by the computer. Only her image on the computer screen disappeared.
III. Paragraph Questions with Answers.
The Computer Swallowed Grandma Poem Explanation Questions 1.
Why was Jeeves called ? Was his visit successful ? Give reasons.
Answer:
Jeeves was called to find out ‘Why grandma was swallowed and consumed by the computer or if she had been caught by a virus or eaten by a worm?’ The computer repairer Jeeves refined the search for grandma everywhere in the computer and in the end, he gave only a negative reply. He said that not only grandma but nothing was found ‘online’. This means that the computer’s internet connection has been snapped for reasons unknown.
The Computer Swallowed Grandma Summary Question 2.
When and how did grandma disappear? Explain the different efforts put by the poet to get back her grandma.
Answer:
The poet’s grandma was an old tech savvy modern lady who lived far away from the poet. They loved each other and often had ‘online’ video chatting. On one such day, grandma mistakenly pressed ‘control’ and ‘enter’ and completely disappeared from the view of the poet on the other end.
The poet took many measures to get back grandma. She searched for grandma in the recycle bin and all the files. She also used the internet to find her. Then the poet called a computer mechanic Jeeves to identify the cause and bringing back grandma, but even that was a failure. Finally the poet desperately requests all the readers of her poem to send grandma back to her if they find her in their ‘inbox’, by email, after copying’, ‘scanning’ and ‘pasting’.
Figures of speech in this poem
1. Personification: the poet personifies the computer to a human being and says it had swallowed/ consumed Grandma.
Line 1 : The computer swallowed grandma.
Line 5 : It devoured her completely.
2. Hyperbole is extravagant exaggeration of an incident. Here the poet exaggerates and says the computer had swallowed and consumed grandma.
Line 1 : The computer swallowed grandma.
Line 5 : It devoured her completely.
3. Pun : It’s a play of words. In the poem the poet writes that her grandma was caught by a virus. Virus means medically a bacteria that causes disease. But in computer it denotes to a defect which erases and destroys the data in it.
Warm up
Look at the picture, discuss in pairs and present it before the class.
If your grandmother is …
The Computer Swallowed Grandma Poem Meaning In Tamil Question 1.
ready for a bicycle race, ______
Answer:
I will go for a race with her.
The Computer Swallowed Grandma Poem Lesson Plan Question 2.
willing to play hide and seek, _______
Answer:
I will play with her.
Question 3.
grabbing a lollipop from you, _______
Answer:
I will give mine to her.

Question 4.
How will you react to these situations?
Answer:
Grandma’s are always a blessing for us. So I would try to fulfill her wishes and make her happy.
The Computer Swallowed Grandma Summary
This childrens poem ‘The Computer Swallowed Grandma, was written by an Anonymous. Ever since it was published in ‘The Daily Mail’ national newspaper in July 2004, it was welcomed the world over for its humour, imagination and language.
The poet was chatting with her grandma online. Suddenly by mistake when grandma presses ‘Control’ and ‘Enter’, her image vanishes from the screen. The upset poet thinks that a virus must have attacked her computer and searches for her in the recycle bin, all files and on the internet. But she couldn’t find grandma, so she calls software engineer Jeeves to search grandma and he too couldn’t find. In the end, the poet requests all the readers of her poem to send grandma by email by copying, scanning and pasting her, if they happen to find grandma in their ‘in-box’.