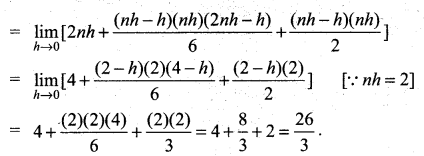Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.2

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.2

Question 1.
Evaluate the following integrals as the limits of sums:

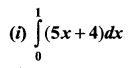
Solution:
We use the formula

(ii) \(\int_{1}^{2}\left(4 x^{2}-1\right) d x\)
Solution:
We use the formula

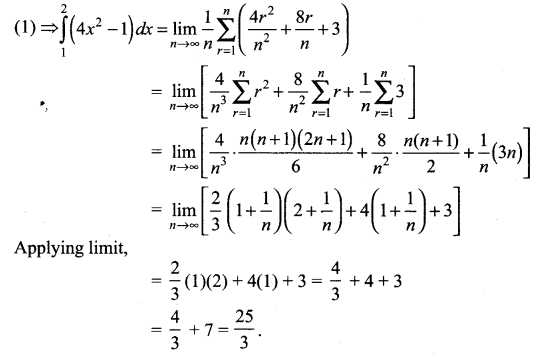
Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.2 Additional Problems

Question 1.
Evaluate as the limit of sums: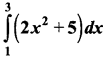
Solution:
Let f(x) = 2x² +5; a = 1; b = 3 and nh = 3 – 1 = 2

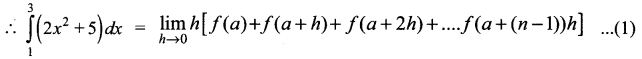
Here, f(a) = f(1) = 2(1)² + 5
f(a + h) = f(1 + h) = 2(1 + h)² + 5
f(a + 2h) = f(1 + 2h) = 2 (1 + 2h)² + 5
f[a+(n – 1)h = f[1 + (n – 1)h] = 2[1 + (n – 1)h]² + 5

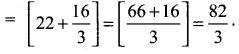
Question 2.
Evaluates as the limit of sums: \(\int_{1}^{2}\left(x^{2}-1\right) d x\)
Solution:
Let f(x) = x² – 1 for 1 ≤ x ≤ 2
We divide the interval [1, 2] into n equal sub-intervals each of length h.
We have a = 1, b = 2

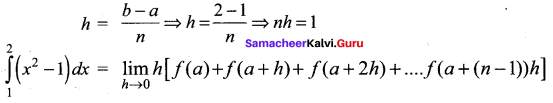
Here, f(a) = f(1) = (1)² – 1 = 0
f(a + h) = f(1 + h) = (1 + h)² – 1 = 1 + h² + 2h – 1 = h² + 2h
f(a + 2h) = f(1 + 2h) = (1 + 2h)² – 1 = 1 + 4h² + 4h – 1 = 4h² + 4h
f[a + (n -1)h] = f[1 + (n – 1)h] = [1 + (n – 1)h]² – 1
= 1 + (n – 1)² h² + 2(n – 1 )h – 1 = (n – 1)² h² + 2 (n – 1 )h

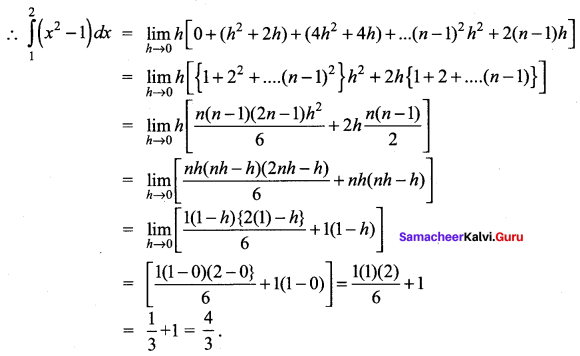
Question 3.
Evalute: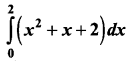
Solution:
Let f(x) = x² + x + 2, for 0 ≤ x ≤ 2 Here, a = 0,b = 2
We divide the closed interval [0, 2] into n subintervals each of length h.

By definition,