You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.4
Question 1.
Find the non-parametric form of vector equation and Cartesian equations of the straight line passing through the point with position vector \(4 \hat{i}+3 \hat{j}-7 \hat{k}\) and parallel to the vector \(2 \hat{i}-6 \hat{j}+7 \hat{k}\)
Solution:
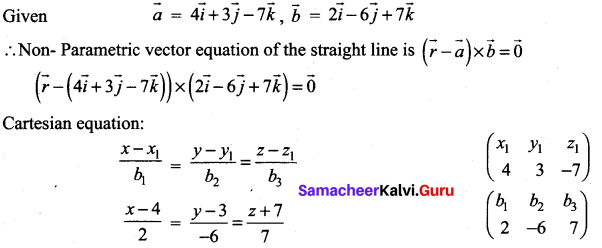
Question 2.
Find the parametric form of vector equation and Cartesian equations of the straight line passing through the point (-2, 3, 4) and parallel to the straight line \(\frac{x-1}{-4}=\frac{y+3}{5}=\frac{8-z}{6}\)
Solution:

Question 3.
Find the points where the straight line passes through (6, 7, 4) and (8, 4, 9) cuts the xz and yz planes.
Solution:
Given straight line passing through the points (6, 7, 4) and (8, 4, 9).
Direction ratio of the straight line joining these two points 2, -3, -5.
Cartesian equation:
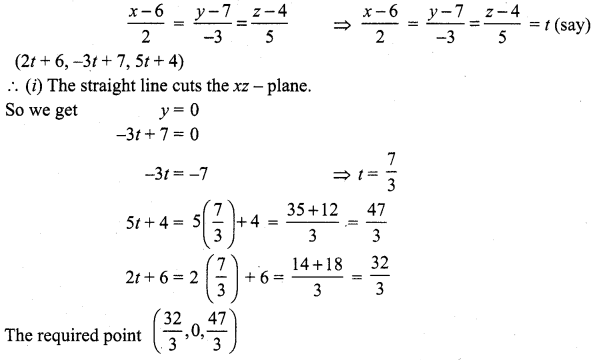
(ii) The straight Line cuts yz-plane
So we get x = 0
2t + 6 = 0 ⇒ 2t = -6
t = -3
-3t + 7 = -3 (-3) + 7 = 9 + 7 = 16
5t + 4 = 5(-3) + 4 = -15 + 4 = -11
The required point (0, 16, -11).
![]()
Question 4.
Find the direction cosines of the straight line passing through the points (5, 6, 7) and (7,9,13). Also, find the parametric form of vector equation and Cartesian equations of the straight line passing through two given points.
Solution:
Given straight line passing through the points (5, 6, 7) and (7, 9, 13)
∴ d.r.s : 2, 3, 6

Note: Selection of \(\vec{a}\) and \(\vec{b}\) is your choice.
Question 5.
Find the acute angle between the following lines.
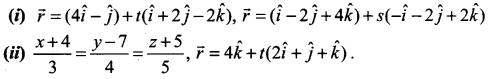
(iii) 2x = 3y = -z and 6x = -y = -4z
Solution:
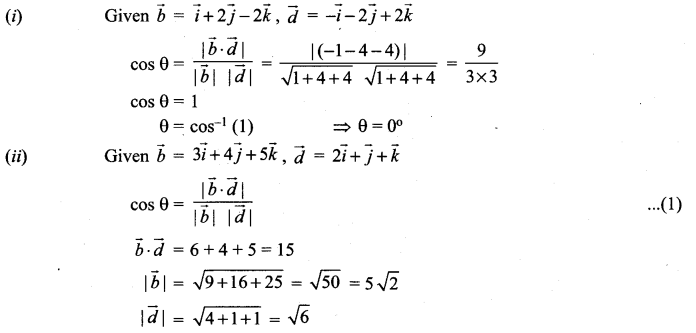

Question 6.
The vertices of ∆ABC are A(7, 2, 1), B(6, 0, 3), and C(4, 2, 4) . Find ∠ABC.
Solution:
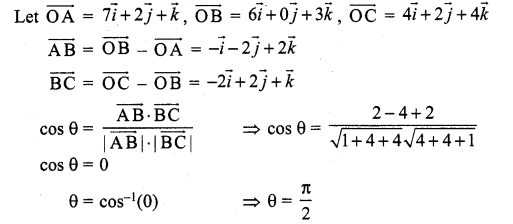
Question 7.
If the straight line joining the points (2, 1, 4) and (a – 1, 4, -1) is parallel to the line joining the points (0, 2, b – 1) and (5, 3, -2), find the values of a and b.
Solution:


Question 8.
If the straight lines ![]() are perpendicular to each other, find the value of m.
are perpendicular to each other, find the value of m.
Solution:
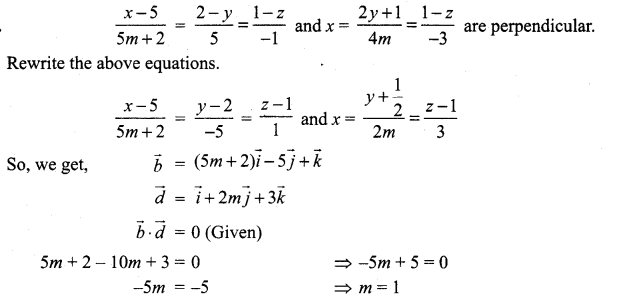
![]()
Question 9.
Show that the points (2, 3, 4),(-1, 4, 5) and (8, 1, 2) are collinear.
Solution:
Given points are (2, 3, 4), (-1, 4, 5) and (8, 1, 2) Equation of the line joining of the first and second point is
\(\frac{x-2}{-3}=\frac{y-3}{1}=\frac{z-4}{1}\) = m (say)
(-3m + 2, m + 3, m + 4)
On putting m = -2, we get the third point is (8, 1, 2)
∴ Given points are collinear.
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.4 Additional Problems
Question 1.
Find the vector and cartesian equations of the straight line passing through the point A with position vector \(3 \vec{i}-\vec{j}+4 \vec{k}\) and parallel to the vector \(-5 \vec{i}+7 \vec{j}+3 \vec{k}\).
Solution:
We know that vector equation of the line through the point with position vector \(\vec{a}\) and parallel to \(\vec{v}\) is given by \(\vec{r}=\vec{a}+t \vec{v}\) where t is a scalar.
Here \(\vec{a}=3 \vec{i}-\vec{j}+4 \vec{k}\) and \(\vec{v}=-5 \vec{i}+7 \vec{j}+3 \vec{k}\)
Vector equation of the line is
\(\vec{r}=(3 \vec{i}-\vec{j}+4 \vec{k})+t(-5 \vec{i}+7 \vec{j}+3 \vec{k})\) ………………. (1)
The cartesian equation of the line passing through (xp yx, zx) and parallel to a vector whose d.r.s are l, m, n is
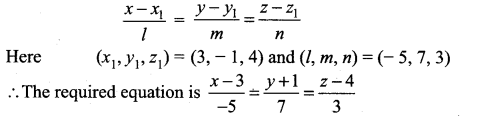
Question 2.
Find the vector and cartesian equations of the straight line passing through the points (- 5, 2, 3) and (4, – 3, 6).
Solution:
Vector equation of the straight line passing through two points with position vectors \(\vec{a}\) and \(\vec{b}\) is given by

Question 3.
Find the angle between the lines.
![]()
Solution:
Let the given lines be in the direction of \(\vec{u}\) and \(\vec{v}\)
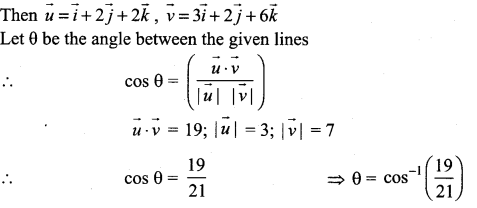
![]()
Question 4.
Find the angle between the following lines 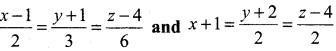
Solution:
Angle between two lines is the same as angle between their parallel vectors.
