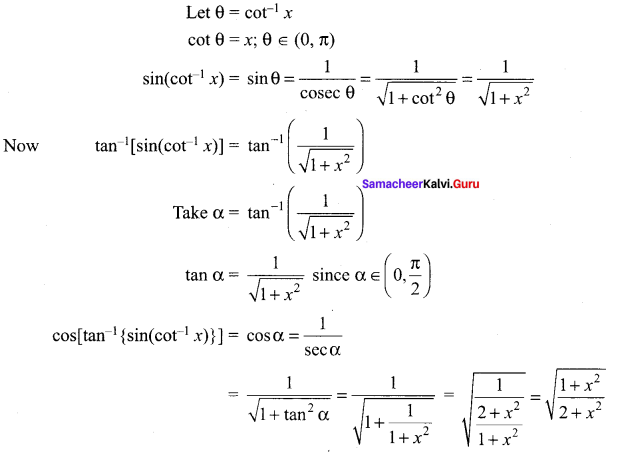You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.5
Question 1.
Find the value, if it exists. If not, give the reason for non-existence.
(i) sin-1(cos π)
(ii) \(\tan ^{-1}\left(\sin \left(-\frac{5 \pi}{2}\right)\right)\)
(iii) sin-1[sin 5]
Solution:
(i) sin-1(cos π) = sin-1(-1) = \(-\frac{\pi}{2}\)
(ii) \(\tan ^{-1}\left(\sin \frac{5 \pi}{2}\right)=\tan ^{-1}\left(-\sin \frac{\pi}{2}\right)=\tan ^{-1}(-1)=-\frac{\pi}{4}\)
(iii) sin-1(sin 5) = sin-1[sin (5 – 2π)] = 5 – 2π
Question 2.
Find the value of the expression in terms of x, with the help of a reference triangle.
(i) sin(cos-1(1 – x))
(ii) cos(tan-1(3x – 1))
(iii) \(\tan \left(\sin ^{-1}\left(x+\frac{1}{2}\right)\right)\)
Solution:
(i) Let cos-1(1 – x) = θ
1 – x = cos θ
We know sin2 θ = 1 – cos2 θ


![]()
Question 3.
Find the value of
(i) \(\sin ^{-1}\left(\cos \left(\sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)\right)\right.\)
(ii) \(\cot \left(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{4}{5}\right)\)
(iii) \(\tan \left(\sin ^{-1} \frac{3}{5}+\cot ^{-1} \frac{3}{2}\right)\)
Solution:
(i) \(\sin ^{-1} \frac{\sqrt{3}}{2}=\frac{\pi}{3} \text { and } \cos \left(\frac{\pi}{3}\right)=\frac{1}{2} \text { and }\)

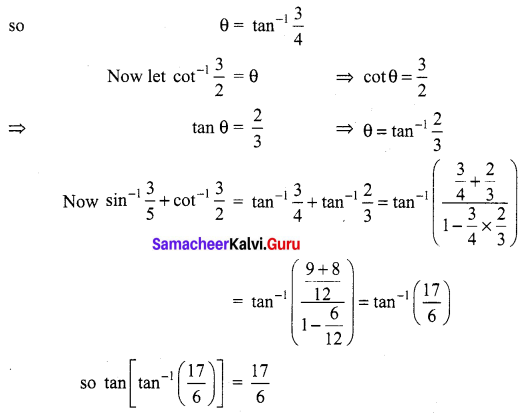
Question 4.
Prove that
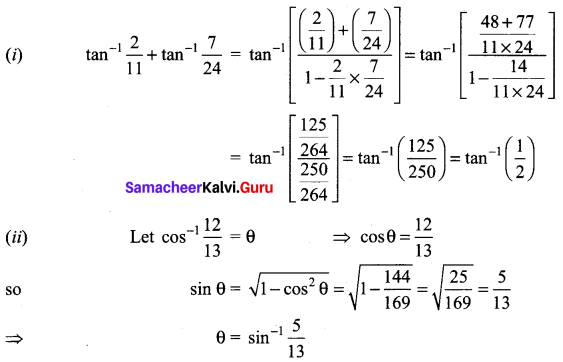
(i) \(\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}\)
(ii) \(\sin ^{-1} \frac{3}{5}-\cos ^{-1} \frac{12}{13}=\sin ^{-1} \frac{16}{65}\)
Solution:

Question 5.
Prove that tan-1 x + tan-1 y + tan-1 z = tan-1 \(\left[\frac{x+y+z-x y z}{1-x y-y z-z x}\right]\)
Solution:

Question 6.
If tan-1 x + tan-1 y + tan-1 z = π, show that x + y + z = xyz.
Solution:
Given tan-1 x + tan-1 y + tan-1 z = π
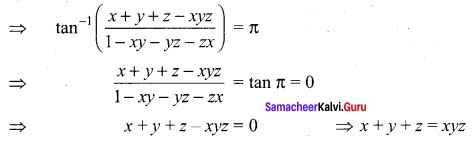
Question 7.
Prove that \(\tan ^{-1} x+\tan ^{-1} \frac{2 x}{1-x^{2}}=\tan ^{-1} \frac{3 x-x^{3}}{1-3 x^{2}},|x|<\frac{1}{\sqrt{3}}\)
Solution:
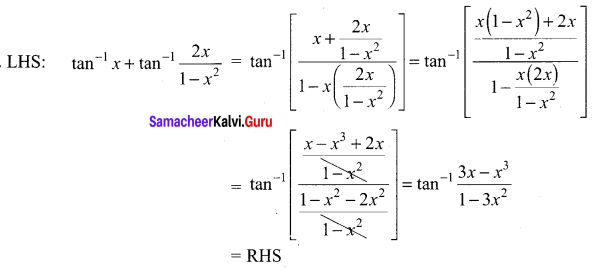
![]()
Question 8.
Simplify: \(\tan ^{-1} \frac{x}{y}-\tan ^{-1} \frac{x-y}{x+y}\)
Solution:
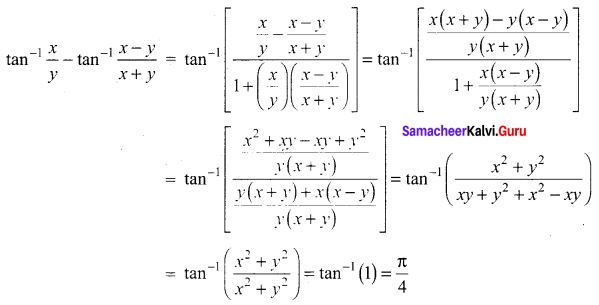
Question 9.
Find the value of
(i) \(\sin ^{-1} \frac{5}{x}+\sin ^{-1} \frac{12}{x}=\frac{\pi}{2}\)
(ii) \(2 \tan ^{-1} x=\cos ^{-1} \frac{1-a^{2}}{1+a^{2}}-\cos ^{-1} \frac{1-b^{2}}{1+b^{2}}\), a > 0, b > 0
(iii) 2 tan-1(cos x) = tarn-1 (2 cosec x)
(iv) cot-1 x – cot-1 (x + 2) = \(\frac{\pi}{12}\), x > 0
Solution:




Question 10.
Find the number of solution of the equation tan-1(x – 1) + tan-1 x + tan-1 (x + 1) = tan-1(3x).
Solution:
tan-1(x – 1) + tan-1 x + tan-1 (x + 1) = tan-1(3x)
tan-1(x – 1) + tan-1 (x + 1) = tan-1 3x – tan-1 x
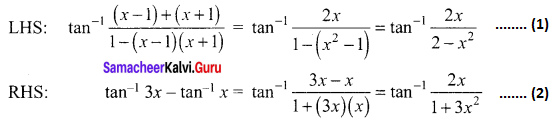
LHS = RHS
⇒ \(\tan ^{-1} \frac{2 x}{2-x^{2}}=\tan ^{-1} \frac{2 x}{1+3 x^{2}}\)
⇒ \(\frac{2 x}{2-x^{2}}=\frac{2 x}{1+3 x^{2}}\)
⇒ 2 – x2 = 1 + 3x2
⇒ 4x2 = 1
⇒ x2 = \(\frac{1}{4}\)
⇒ x = ±\(\frac{1}{2}\)
So, the equation has 2 solutions.
Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.5 Additional Questions
Question 1.
Solve the following equation: sin-1(1 – x) – 2 sin-1 x = \(\frac{\pi}{2}\)
Solution:
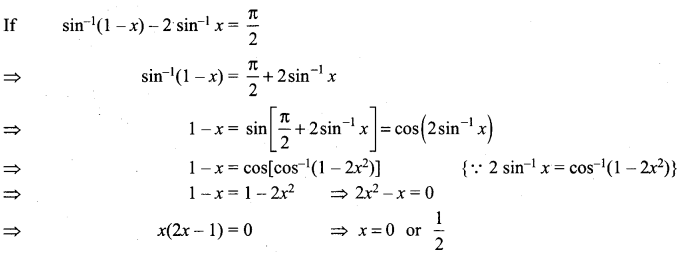
![]()
Question 2.
Solve: tan-1 2x + tan-1 3x = \(\frac{\pi}{4}\)
Solution:
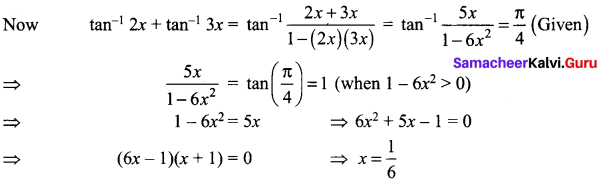
Question 3.
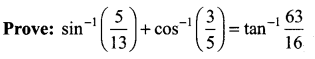
Solution:
Do it yourself
Question 4.
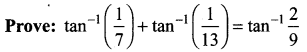
Solution:
Do it yourself
Question 5.
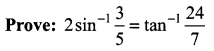
Solution:
Do it yourself
Question 6.
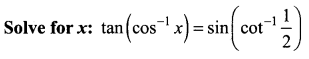
Solution:
Do it yourself
Question 7.
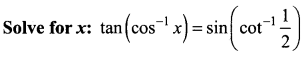
Solution:
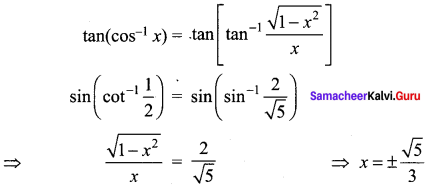
![]()
Question 8.
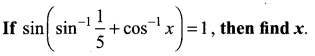
Solution:

Question 9.
![]()
Solution:
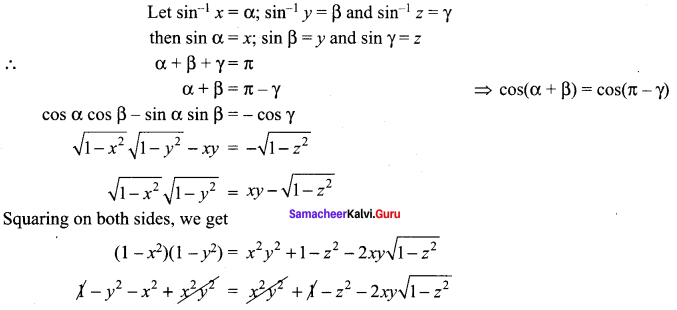
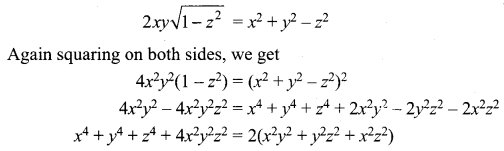
Question 10.
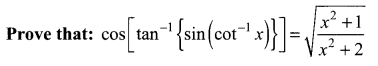
Solution: