You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.7
Question 1.
Solve the following system of homogeneous equations.
(i) 3x + 2y + 7z = 0, 4x – 3y – 2z = 0, 5x + 9y + 23z = 0
(ii) 2x + 3y – z = 0, x – y – 2z = 0, 3x + y + 3z = 0
Solution:
(i) The matrix form of the above equations is
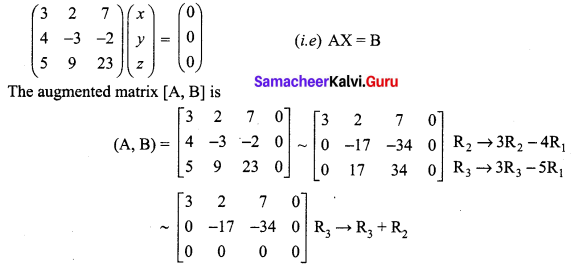
The above matrix is in echelon form.
Here ρ(A, B) = ρ(A) < number of unknowns.
The system is consistent with infinite number of solutions. To find the solutions.
Writing the equivalent equations.
We get 3x + 2y + 7z = 0 ……. (1)
-17y – 34z = 0 ……. (2)
Taking z = t in (2) we get -17y – 34t = 0
⇒ -17y = 34t
⇒ y = -2t
Taking z = t, y = -2t in (1) we get
3x + 2(-2t) + 7t = 0
⇒ 3x – 4t + 7t = 0
⇒ 3x = -3t
⇒ x = -t
So the solution is x = -t; y = -2t; and z = t, t ∈ R
(ii) The matrix form of the equations is
\(\left(\begin{array}{ccc}{2} & {3} & {-1} \\ {1} & {-1} & {-2} \\ {3} & {1} & {3}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{0} \\ {0} \\ {0}\end{array}\right)\)
(i.e) AX = B
The augmented matrix [A, B] is

The above matrix is in echelon form also ρ(A, B) = ρ(A) = 3 = number of unknowns
The system is consistent with unique solution, x = y = z = 0
(i.e) The system has trivial solution only.
![]()
Question 2.
Determine the values of λ for which the following system of equations.
x + y + 3z = 0, 4x + 3y + λz = 0, 2x +y + 2z = 0 has
(i) a unique solution
(ii) a non-trivial solution
Solution:
The matrix form of the equation is
\(\left(\begin{array}{lll}{1} & {1} & {3} \\ {4} & {3} & {\lambda} \\ {2} & {1} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{0} \\ {0} \\ {0}\end{array}\right)\)
(i.e) AX = B
The augmented matrix [A, B] is
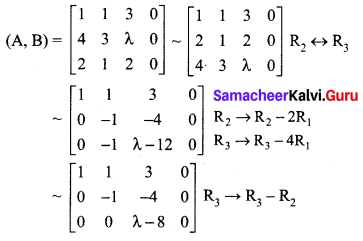
The above matrix is in echelon form
Case 1: When λ ≠ 8, ρ(A, B) = ρ(A) = 3 = number of unknowns
The system is consistent with a unique solution.
Case 2: When λ = 8, ρ(A, B) = ρ(A) = 2 < number of unknowns.
The system is consistent with non-trivial solutions.
Question 3.
By using the Gaussian elimination method, balance the chemical reaction equation:
C2H6 + O2 → H2O + CO2
Solution:
We are searching for positive integers x1, x2, x3 and x4 such that
x1C2H6 + x2O2 = x3H2O + x4CO2 ……. (1)
The number of carbon atoms on LHS of (1) should be equal to the number of carbon atoms on the RHS of (1).
So we get a linear homogeneous equation.
2x1 = x4
⇒ 2x1 – x4 = 0 …… (2)
Similarly considering hydrogen and oxygen atoms we get respectively.
2x2 = x3 + 2x4
⇒ 2x2 – x3 – 2x4 = 0 …… (3)
and -2x3+ 3x4 = 0 …… (4)
Equations (2), (3) and (4) constitute a homogeneous system of linear equations in four unknowns.
The augmented matrix (A, B) is
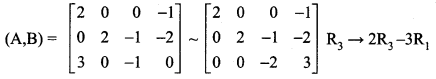
Now ρ(A, B) = ρ(A) = 3 < number of unknowns.
So the system is consistent and has an infinite number of solutions.
Writing the equations using the echelon form we get
2x1 – x4 = 0 …… (5)
2x2 – x3 – 2x4 = 0 ……. (6)
-2x3 + 3x4 = 0 ……. (7)

Since x1, x2, x3 and x4 are positive integers. Let us choose t = 4t.
Then we get x1 = 2, x2 = 7, x3 = 6, and x4 = 4
So the balanced equation is 2C2H6 + 7O2 → 6H2O + 4CO2.
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.7 Additional Problems
Question 1.
Solve the following homogeneous linear equations.
x + 2y – 5z = 0,
3x + 4y + 6z = 0,
x + y + z = 0
Solution:
The given system of equations can be written in the form of matrix equation
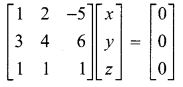
AX = B
The augmented matrix is

This is in the echelon form.
Clearly ρ[A, B] = 3 and ρ(A) = 3
∴ ρ(A) = ρ[A, B] = 3 = number of unknowns
∴ The given system of equations is consistent and has a unique solution. i.e., trivial solution
∴ x = 0, y = 0 and z = 0
Note: Since ρ(A) = 3, | A | ≠ 0 i.e. A is non-singular;
∴ The given system has only trivial solution x = 0, y = 0, z = 0
Question 2.
For what value of n the equations.
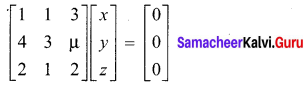
x + y + 3z = 0,
4x + 3y + µz = 0,
2x + y + 2z = 0 have a
(i) trivial solution,
(ii) non-trivial solution.
Solution:
The system of equations can be written as AX = B
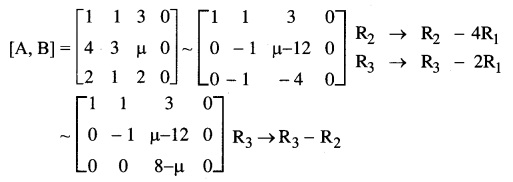
![]()
Case (i): If µ ≠ 8 then 8 – µ ≠ 0 and hence there are three non-zero rows.
∴ ρ[A] = ρ[A, B] = 3 = the number of unknowns.
∴ The system has the trivial solution x = 0, y = 0, z = 0
Case (ii): If µ = 8 then.
ρ[A, B] = 2 and ρ(A) = 2
∴ ρ(A) = ρ[A, B] = 2 < number of unknowns.
The given system is equivalent to
x + y + 3z = 0; y + 4z = 0
∴ y= – 4z ; x = z
Taking z = k, we get x = k,y = – 4k, z = k [k ∈ R – {0}] which are non-trivial solutions.
Thus the system is consistent and has infinitely many non-trivial solutions.
Note: In case (ii) the system also has trivial solution. For only non-trivial solutions we removed k = 0.