You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.4
Question 1.
Solve the following systems of linear equations by Cramer’s rule:
(i) 5x – 2y + 16 = 0, x + 3y – 7 = 0
(ii) \(\frac{3}{x}+2 y=12, \frac{2}{x}+3 y=13\)
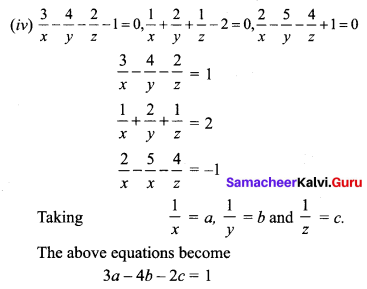
(iii) 3x + 3y – z = 11, 2x – y + 2z = 9, 4x + 3y + 2z = 25
![]()
Solution:
(i) 5x – 2y + 16 = 0, x + 3y – 7 = 0
The above equations are 5x – 2y = -16 and x + 3y = -7
The matrix form of two above equations is
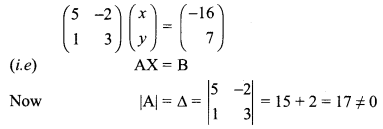

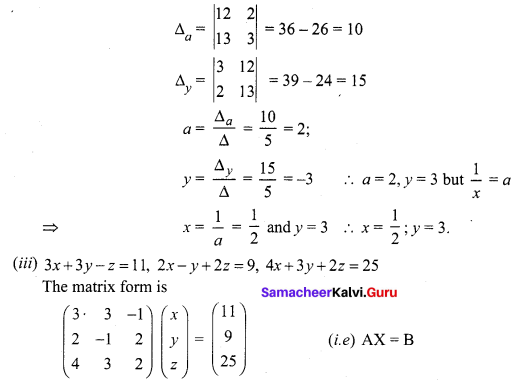



![]()
Question 2.
In a competitive examination, one mark is awarded for every correct answer while \(\frac { 1 }{ 4 }\) mark is deducted for every wrong answer. A student answered 100 questions and got 80 marks. How many questions did he answer correctly? (Use Cramer’s rule to solve the problem).
Solution:
No. of Questions answered = 100
Let the No. of questions answered correctly be x and the No. of questions answered wrongly be y
Here, x + y = 100 and x – \(\frac { 1 }{ 4 }\) y = 80
(i.e) x + y = 100 and 4x – y = 320
The matrix form is

No. of questions answered correctly x = 84.
Question 3.
A chemist has one solution which is 50% acid and another solution which is 25% acid. How much each should be mixed to make 10 litres of a 40% acid solution? (Use Cramer’s rule to solve the problem).
Solution:
Let the no. of litres in 50% acid used be x litres and the no. of litres in 25% acid used be y litres
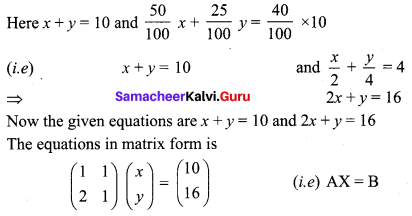
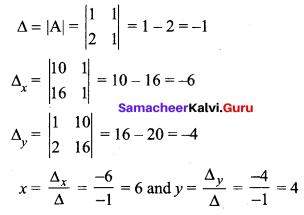
(i.e) we have to mix 6 litres in 50% acid and 4 litres in 25% acid.
Question 4.
A fish tank can be filled in 10 minutes using both pumps A and B simultaneously. However, pump B can pump water in or out at the same rate. If pump B is inadvertently run in reverse, then the tank will be filled in 30 minutes. How long would it take each pump to fill the tank by itself? (Use Cramer’s rule to solve the problem).
Solution:
Time is taken for pump A to fill the tank be x minutes and time taken for pump B to fill the tank be y minutes


(i.e) Pump A can fill the tank in 15 minutes and pump B can fill the tank in 30 minutes.
![]()
Question 5.
A family of 3 people went out for dinner in a restaurant. The cost of two dosai, three idlies and two vadais is ₹ 150. The cost of the two dosai, two idlies and four vadais is ₹ 200. The cost of five dosai, four idlies and two vadais is ₹ 250. The family has ₹ 350 in hand and they ate 3 dosai and six idlies and six vadais. Will they be able to manage to pay the bill within the amount they had?
Solution:
Let the cost of 1 dosai be ₹ x the cost of 1 idli be ₹ y and the cost of 1 vadai be ₹ z
Here 2x + 3y + 2z = 150
2x + 2y + 4z = 200
5x + 4y + 2z = 250
Writing the above equations in matrix form


So, cost of 1 dosai = x = ₹ 30
cost of 1 idli = y = ₹ 10 and
cost of 1 vadai = z = ₹ 30
Now cost of 3 dosai and 6 idlis and 6 vadais = 3 × 30 + 6 × 10 + 6 × 30 = 90+ 60+ 180 = ₹ 330
and they are having ₹ 350. So they will be able to manage to pay the bill.
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.4 Additional Problems
Question 1.
Solve the following non-homogeneous system of linear equations by determinant method: 3x + 2y = 5, x + 3y = 4.
Solution:

Solution is (x, y) = (1, 1).
Question 2.
Solve the following non-homogeneous system of linear equations by determinant method: x + y + z = 4 ; x – y + z = 2 ; 2x + y – z = 1
Solution:
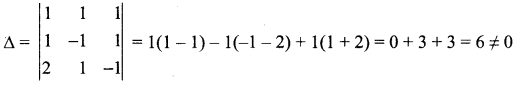
Since ∆ ≠ 0, the system has unique solution

Solution is x, y, z = 1, 1, 2
Question 3.
Solve the following non-homogeneous system of linear equations by determinant method: 3x + y – z = 2; 2x – y + 2z = 6; 2x + y – 2z = -2
Solution:

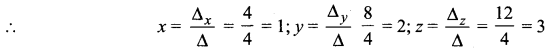
Solution is x, y, z = 1, 2, 3
![]()
Question 4.
Solve the following non-homogeneous system of linear equations by determinant method:
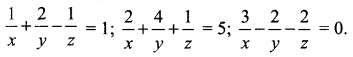
Solution:
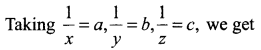
a + 2b – c = 1 … (1)
2a + 4b + c = 5 ….. (2)
3a – 2b – 2c = 0 …… (3)
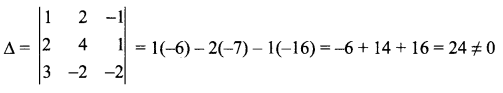
∴ The system has unique solution.
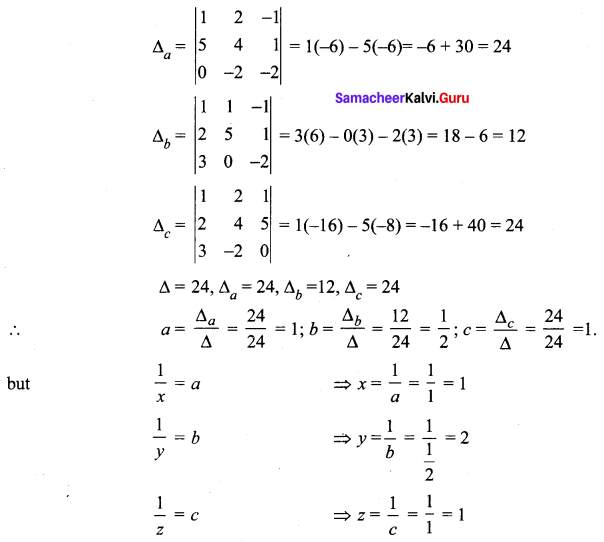
∴ Solution is x, y, z = 1, 2, 1.