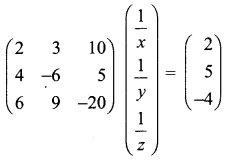You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.3
Question 1.
Solve the following system of linear equations by matrix inversion method:
(i) 2x + 5y = -2, x + 2y = -3
(ii) 2x – y = 8, 3x + 2y = -2
(iii) 2x + 3y – z = 9, x + y + z = 9, 3x – y – z = -1
(iv) x + y + z – 2 = 0, 6x – 4y + 5z – 31 = 0, 5x + 2y + 2z = 13
Solution:
(i) 2x + 5y = -2, x + 2y = -3
The matrix form of the above equations is \(\left(\begin{array}{ll}{2} & {5} \\ {1} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y}\end{array}\right)=\left(\begin{array}{l}{-2} \\ {-3}\end{array}\right)\)
(i.e) AX = B

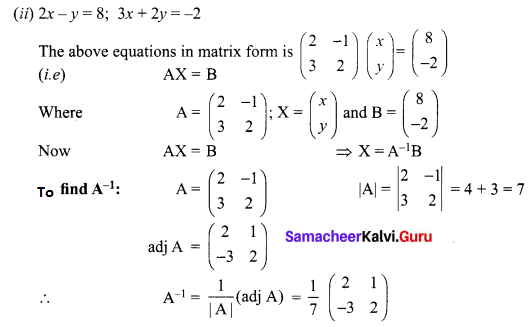




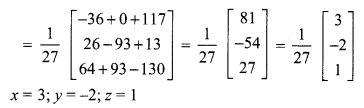
![]()
Question 2.
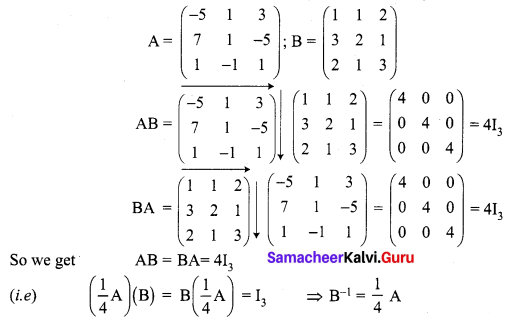
If A = \(\left[\begin{array}{ccc}{-5} & {1} & {3} \\ {7} & {1} & {-5} \\ {1} & {-1} & {1}\end{array}\right]\) and B = \(\left[\begin{array}{lll}{1} & {1} & {2} \\ {3} & {2} & {1} \\ {2} & {1} & {3}\end{array}\right]\) find the products AB and BA and hence solve the system of equations x + y + 2z = 1, 3x + 2y + z = 7, 2x + y + 3z = 2.
Solution:

Question 3.
A man is appointed in a job with a monthly salary of certain amount and a fixed amount of annual increment. If his salary was ₹ 19,800 per month at the end of the first month after 3 years of service and ₹ 23,400 per month at the end of the first month after 9 years of service, find his starting salary and his annual increment. (Use matrix inversion method to solve the problem.)
Solution:
Let his monthly salary be ₹ x and his annual increment be ₹ y
Given x + 3y = 19800 and x + 9y = 23400
Writing the above equations in matrix form, we get
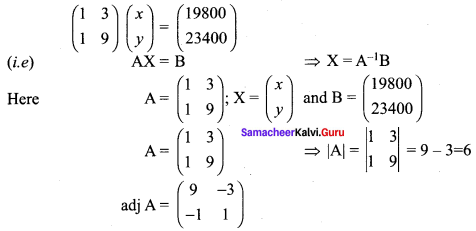
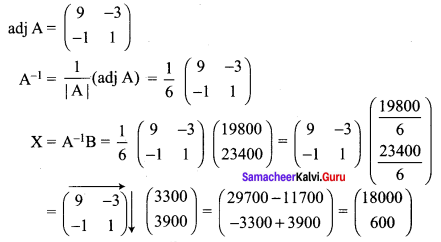
x = ₹ 18000 and y = ₹ 600
(i.e) monthly salary = ₹ 18000 and annual increment = ₹ 600
Question 4.
4 men and 4 women can finish a piece of work jointly in 3 days while 2 men and 5 women can finish the same work jointly in 4 days. Find the time taken by one man alone and that of one woman alone to finish the same work by using matrix inversion method.
Solution:
Let the work done by man in 1 day be x and the work done by a woman in 1 day be y
Now we are given
4x + 4y = \(\frac { 1 }{ 3 }\) ⇒ 12x + 12y = 1
and 2x + 5y = \(\frac { 1 }{ 4 }\) ⇒ 8x + 20y = 1
The matrix form of the above equations is \(\left(\begin{array}{cc}{12} & {12} \\ {8} & {20}\end{array}\right)\left(\begin{array}{l}{x} \\ {y}\end{array}\right)=\left(\begin{array}{l}{1} \\ {1}\end{array}\right)\)
(i.e) AX = B ⇒ X = A-1B
Here
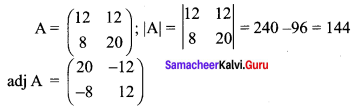
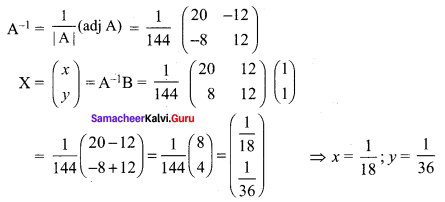
(i.e) The work done by a man in 1 day = x = \(\frac{1}{18}\)
The time taken by a man to finish the work = 18 days.
The work done by a woman in 1 day = y = \(\frac{1}{36}\)
The time is taken by a woman to finish the work = 36 days.
Question 5.
The prices of three commodities A, B and C are ₹ x, y and z per units respectively. A person P purchases 4 units of B and sells two units of A and 5 units of C. Person Q purchases 2 units of C and sells 3 units of A and one unit of B . Person R purchases one unit of A and sells 3 unit of B and one unit of C. In the process, P, Q and R earn ₹ 15,000, ₹ 1,000 and ₹ 4,000 respectively. Find the prices per unit of A,B and C. (Use matrix inversion method to solve the problem.)
Solution:
Price of A = ₹ x /unit
Price of B = ₹ y /unit
Price of C = ₹ z /unit
We are given
2x – 4y + 5z = 15000
3x + y – 2z = 1000
-x + 3y + z = 4000
The matrix form of the above equations is \(\left(\begin{array}{rrr}{2} & {-4} & {5} \\ {3} & {1} & {-2} \\ {-1} & {3} & {1}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{r}{15000} \\ {1000} \\ {4000}\end{array}\right)\)
(i.e) AX = B ⇒ X = A-1B
Here

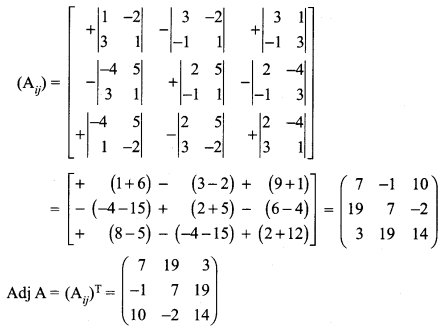

![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.3 Additional Problems
Question 1.
Using matrix method, solve the following system of equations:
x + 2y + z = 7, x + 3z = 11, 2x – 3y = 1
Solution:
The system of equations can be written in the form AX = B, where
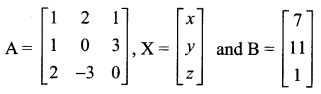

= 9 + 12 – 3 = 18 ≠ 0 Non-singular matrix.
A11 = (0 + 9) = 9, A12 = -(0 – 6) = 6,
A13 = (-3 – 0) = -3
A21 = – (0 + 3) = -3, A22 = (0 – 2) = -2
A23 = -(-3 – 4) = 7
A31 = (6 – 0) = 6, A32 = -(-3 – 1) = -2,
A33 = (0 – 2) = -2
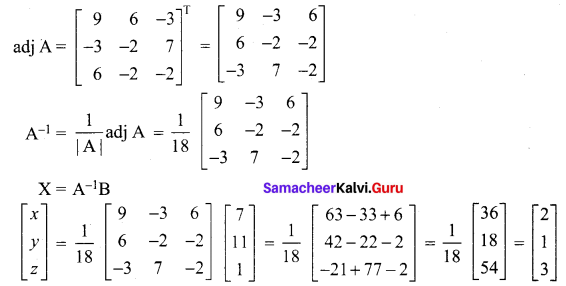
Thus x = 2 ,y = 1 and z = 3.
Question 2.
Using matrices, solve the following system of linear equations: x + 2y – 3z = -4, 2x + 3y + 2z = 2, 3x – 3y – 4z = 11.
Solution:
The system of equations can be written in the form AX = B, where


Thus x = 3,
y = -2 and z = 1
![]()
Question 3.
If 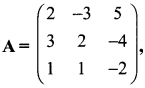 Find A-1. Hence using A-1 solve the system of equations.
Find A-1. Hence using A-1 solve the system of equations.
2x – 3y + 5z = 11,
3x + 2y – 4z = -5,
x + y – 2z = -3.
Solution:

Question 4.
Use product 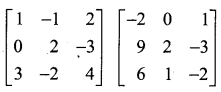 to solve the system of equations
to solve the system of equations
x + 3z = 9,
-x + 2y – 2z = 4,
2x – 3y + 4z = -3
Solution:

Question 5.
Use product 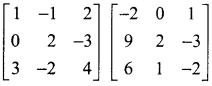 to solve the system of equations
to solve the system of equations
x – y + 2z = 1,
2y – 3z = 1,
3x – 2y + 4z = 2
Solution:

The system of equations can be written in the form AX = C, where

Question 6.
An amount of ₹ 7000 is invested in three types of investments x, y and z at the rate of 3%, 4% and 5% interest respectively. The total annual income is ₹ 280. If the combined income from x and y is ₹ 80 more than that from z, then
(i) Represent the above situation in form of linear equations .
(ii) Is it possible to frame the given linear equations in the form of matrix to obtain the three values x, y and z using matrix multiplication? If yes, find.
(iii) Which value is more beneficial to invest?
Solution:

⇒ -40 + 30 + 0 = -10 ≠ 0
Cofactors C11 = +(-20 – 20) = -40
C21 = -(5 – 4) = 9
C31 = +(5 – 4) = 1
C12 = +(-15 – 15) = -30
C22 = +(-5 – 3) = -8
C32 = -(5 – 3) = -2
C13 = +(12 – 12) = 0
C23 = -(4 – 3) = -1
C33 = +(4 – 3) = 1

Thus, the three values x = ₹ 2000, y = ₹ 3000 and z = ₹ 2000
(iii) The value of y is more beneficial to invest
Question 7.

Solution:

In matrix form