Samacheer Kalvi 12th Maths Guide Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.10

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.10 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.10

கொடுக்கப்பட்ட நான்கு மாற்குவிடைகளிலிருந்து சரியான அல்லது மிகவும் ஏற்புடைய விடையினைத் தேர்ந்தெடுக்கவும்:

கேள்வி 1.
\(\int_{0}^{\frac{2}{3}} \frac{d x}{\sqrt{4-9 x^{2}}}\)_இன் மதிப்பு
(1) \(\frac{\pi}{6}\)
(2) \(\frac{\pi}{2}\)
(3) \(\frac{\pi}{4}\)
(4) π
விடை:
(1) \(\frac{\pi}{6}\)
குறிப்பு:

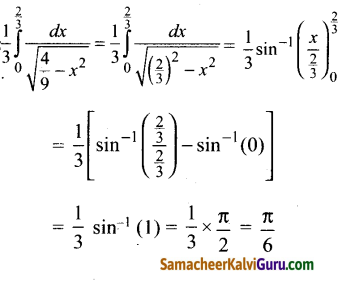
கேள்வி 2.
\(\int_{-1}^{2}|x| d x\) இன் மதிப்பு
(1) \(\frac{1}{2}\)
(2) \(\frac{3}{2}\)
(3) \(\frac{5}{2}\)
(4) \(\frac{7}{2}\)
விடை:
(3) \(\frac{5}{2}\)

குறிப்பு:

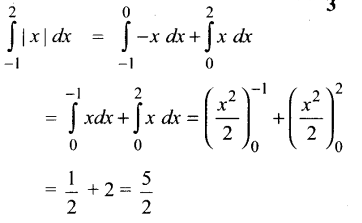
கேள்வி 3.
ஒவ்வொருா ℤ-க்கும்) \(\int_{0}^{\pi} e^{\cos ^{2} x} \cos ^{3}[(2 n+1) x]\) இன் மதிப்பு –
(1) \(\frac{\pi}{2}\)
(2) π
(3) 0
(4) 2
விடை:
(3) 0

குறிப்பு:
\(\int_{0}^{\pi} e^{\cos ^{2} x} \cos ^{3}[(2 n+1) x]\)
e ^cos2s cos³ [(2n + 1)x] என்க
f(-x) = e^cost(-x)2 cos³[(2n + 1)(-x)]
= e^cosx2 – cos³[(2n + 1)x]
= – f (x)
∴ f(x) ஒரு ஒற்றைச் சார்பு

கேள்வி 4.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\) sin² x cosx dx இன் மதிப்பு
(1) \(\frac{3}{2}\)
(2) \(\frac{1}{2}\)
(3) 0
(4) \(\frac{2}{3}\)
விடை:
(4) \(\frac{2}{3}\)

குறிப்பு:

கேள்வி 5.
\(\int_{-4}^{4}\left[\tan ^{-1}\left(\frac{x^{2}}{x^{4}+1}\right)+\tan ^{-1}\left(\frac{x^{4}+1}{x^{2}}\right)\right] d x\) இன் மதிப்பு
(1) π
(2) 2π
(3) 3π
(4) 4π
விடை:
(4) 4π

குறிப்பு:

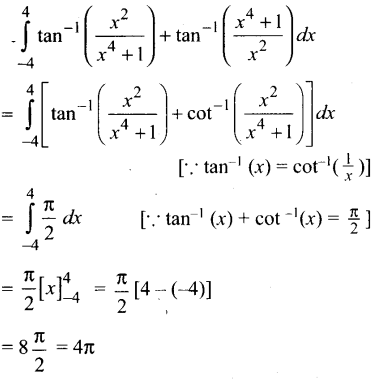
கேள்வி 6.
\(\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\left(\frac{2 x^{7}-3 x^{5}+7 x^{3}-x+1}{\cos ^{2} x}\right) d x\) இன் மதிப்பு
(1) 4
(2) 3
(3) 2
(4) 0
விடை:
(3) 2

குறிப்பு:

[∵ இவைகள் ஒற்றைச் சார்புகள்]
= \([\tan x]_{-\frac{\pi}{4}}^{\frac{\pi}{4}}=\tan \left(\frac{\pi}{4}\right)-\tan \left(-\frac{\pi}{4}\right)\)
= 1 – (-1) = 2

கேள்வி 7.
\(\int_{0}^{x}\) t cos t dt, எனில் \(\frac{d f}{d x}\)
(1) cos x-x sin x
(2) sin x+x cos x
(3) x cos x
(4) x sin x
விடை:
(3) x cos x

குறிப்பு:
\(\int_{0}^{x}\) t cos t dt
\(\frac{d f}{d x}=\frac{d}{d x}\left(\int_{0}^{x} t \cos t d t\right)\) = x cos x
[தொகை நுண்கணிதத்தின் முதலாம் அடிப்படை தேற்றத்தை பயன்படுத்தி]

கேள்வி 8.
y² = 43 என்ற பரவளையத்திற்கும் அதன் செவ்வகலத்திற்கும் இடையே பரப்பானது
(1) \(\frac{2}{3}\)
(2) \(\frac{4}{3}\)
(3) \(\frac{8}{3}\)
(4) \(\frac{5}{3}\)
விடை:
(3) \(\frac{8}{3}\)

குறிப்பு:

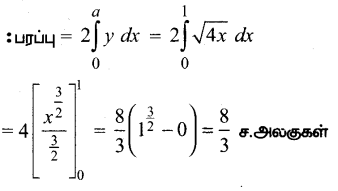
கேள்வி 9.
\(\int_{0}^{x}\) x (1 – x)⁹⁹ dx இன் மதிப்பு
(1) \(\frac{1}{11000}\)
(2) \(\frac{1}{10100}\)
(3) \(\frac{1}{10010}\)
(4) \(\frac{1}{10001}\)
விடை:
(2) \(\frac{1}{10100}\)

குறிப்பு:

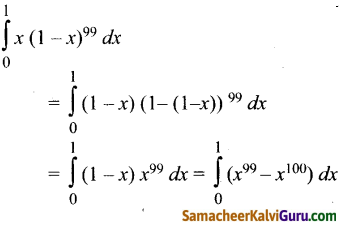
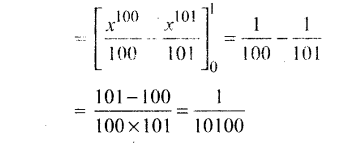
கேள்வி 10.
\(\int_{0}^{\pi} \frac{d x}{1+5^{\cos x}}\) இன் மதிப்பு
(1) \(\frac{\pi}{2}\)
(2) π
(3) \(\frac{3\pi}{2}\)
(4) 2π
விடை:
(1) \(\frac{\pi}{2}\)

கேள்வி 11.
\(\frac{\Gamma(n+2)}{\Gamma(n)}\) = 90 எனில் 10 இன் மதிப்பு
(1) 10
(2) 5
(3) 8
(4) 9
விடை:
(4) 9

குறிப்பு:
⇒ \(\frac{\Gamma(n+2)}{\Gamma(n)}\) = 90
⇒ \(\frac{(n+1) \Gamma(n+1)}{\Gamma(n)}\) = 90
⇒ \(\frac{(n+1)(n) \Gamma(n)}{\Gamma(n)}\) = 90
⇒ n² + n – 90 = 0
⇒ (n + 10) (n – 9) = 10, 9
⇒ n = 9

கேள்வி 12.
\(\int_{0}^{\frac{\pi}{6}}\) cos³ 3 x dx இன் மதிப்பு
(1) \(\frac{2}{3}\)
(2) \(\frac{2}{9}\)
(3) \(\frac{1}{9}\)
(4) \(\frac{1}{3}\)
விடை:
(2) \(\frac{2}{9}\)

குறிப்பு:

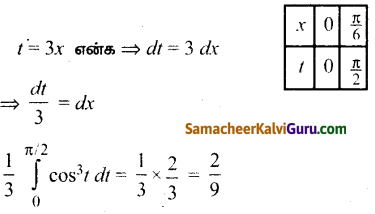
கேள்வி 13.
\(\int_{0}^{\pi}\) sin⁴ x dx இன் மதிப்பு
(1) \(\frac{3\pi}{10}\)
(2) \(\frac{3\pi}{8}\)
(3) \(\frac{3\pi}{4}\)
(4) \(\frac{3\pi}{2}\)
விடை:
(2) \(\frac{3\pi}{8}\)

குறிப்பு:

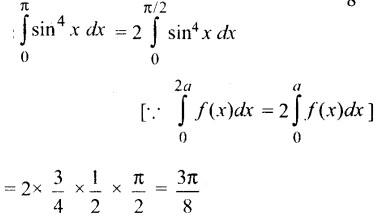
கேள்வி 14.
\(\int_{0}^{\infty}\) e^-3x x² dx இன் மதிப்பு
(1) \(\frac{7}{27}\)
(2) \(\frac{5}{27}\)
(3) \(\frac{4}{27}\)
(4) \(\frac{2}{27}\)
விடை:
(4) \(\frac{2}{27}\)

^{குறிப்பு:}

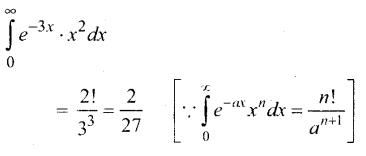
கேள்வி 15.
\(\int_{a}^{a} \frac{1}{4+x^{2}} d x=\frac{\pi}{8}\)எனில் 14 இன் மதிப்பு
(1) 4
(2) 1
(3) 3
(4) 2
விடை:
(4) 2

குறிப்பு:

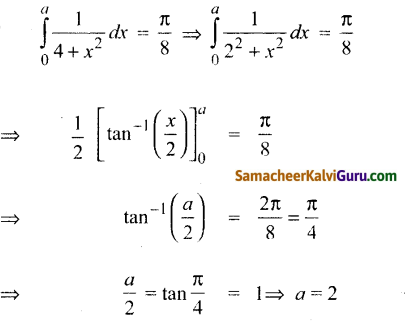
கேள்வி 16.
y² = x(a – x) என்ற வளைவரையில் அடைபடும் அரங்கத்தின் பரப்பை x- அச்சைப் பொருத்து சுழற்றுவதால் உருவாகும் திடப்பொருளின் கன அளவு
(1) πa³
(2) \(\frac{\pi a^{3}}{4}\)
(3) \(\frac{\pi a^{2}}{5}\)
(4) \(\frac{\pi a^{3}}{6}\)
விடை:
(4) \(\frac{\pi a^{3}}{6}\)

குறிப்பு:
கன அளவு

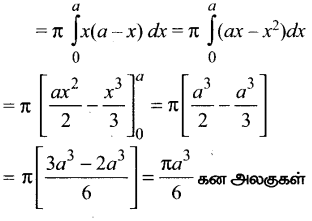
கேள்வி 17.
f(x) = \(\int_{1}^{x} \frac{e^{\sin u}}{u} d u\), x > 1 மற்றும் \(\int_{1}^{3} \frac{e^{\sin x^{2}}}{x} d x=\frac{1}{2}[f(a)-f(1)]\) எனில் பெறக்கூடிய ஒரு மதிப்பு
(1) 3
(2) 6
(3) 9
(4) 5
விடை:
(3) 9

குறிப்பு:

கேள்வி 18.
\(\) (sin^-1x)² இன் மதிப்பு
(1) \(\frac{\pi^{2}}{4}\) – 1
(2) \(\frac{\pi^{2}}{4}\) + 2
(3) \(\frac{\pi^{2}}{4}\) + 1
(4) \(\frac{\pi^{2}}{4}\) – 2
விடை:
(4) \(\frac{\pi^{2}}{4}\) – 2

குறிப்பு:

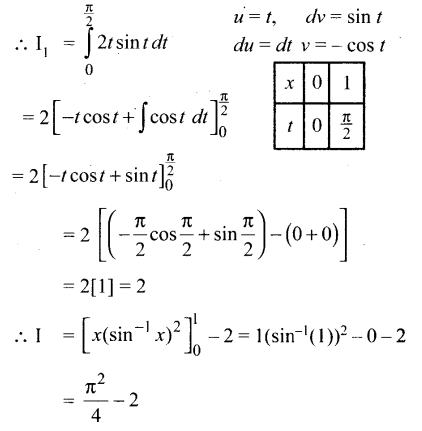
கேள்வி 19.
\(\int_{0}^{a}\left(\sqrt{a^{2}-x^{2}}\right)^{2} d x\) இன் மதிப்பு

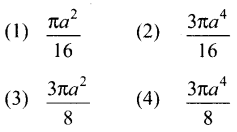
விடை:
(2) \(\frac{3 \pi a^{4}}{16}\)

குறிப்பு:
I = \(\int_{0}^{a}\left(\sqrt{a^{2}-x^{2}}\right)^{2} d x\)
x = a sin θ என பிரதியிட ⇒ dx = a cos θ dθ

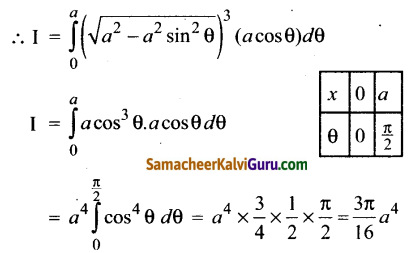
கேள்வி 20.
\(\int_{0}^{x} f(t) d t=x+\int_{x}^{1} t f(t) d t\), எனில் f(1) இன் மதிப்பு
(1) \(\frac{1}{2}\)
(2) 2
(3) 1
(4) \(\frac{3}{4}\)
விடை:
(1) \(\frac{1}{2}\)

குறிப்பு:
\(\int_{0}^{x} f(t) d t=x+\int_{x}^{1} t f(t) d t\)
இருபுறமும் X-ஐ பொறுத்து வகைப்படுத்த கிடைப்பது
f(x) = 1 – x f (x)
∴ f(1) = 1- f (1)
2f(1) = 1
f(1) = \(\frac{1}{2}\) [தொகை நுண் கணிதத்தின் முதலாம் அடிப்படை தேற்றத்தை பயன்படுத்தி]