Samacheer Kalvi 12th Maths Guide Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.2

கேள்வி 1.
பின்வரும் சார்புகளுக்கு வகையீடு dy காண்க :
(i) y = \(\frac{(1-2 x)^{3}}{3-4 x}\)
(ii) y = (3 + sin(2x))^{\(\frac{2}{3}\)}
(iii) y = e^x2-5x+7 cos (x² – 1)
தீர்வு:
y = \(\frac{(1-2 x)^{3}}{3-4 x}\)
கொடுக்கப்பட்ட y = \(\frac{(1-2 x)^{3}}{3-4 x}\)
வகையீடு எடுக்க

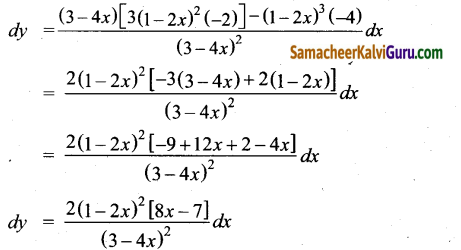
(ii) y = (3+sin(2x))^{\(\frac{2}{3}\)}
கொடுக்கப்பட்ட y = (3+sin(2x))^{\(\frac{2}{3}\)}
வகையீடு எடுக்க
dy = \(\frac{2}{3}(3+\sin 2 x)^{\frac{2}{3}-1}(\cos 2 x)(2) d x\)
dy = \(\frac{4}{3} \cdot \frac{\cos 2 x}{(3+\sin 2 x)^{\frac{1}{3}}} d x\)

(iii) y = e^{x2 – 5x + 7} cos (x² – 1)
கொடுக்கப்பட்ட y = e^{x2 – 5x + 7} cos (x² – 1)
வகையீடு எடுக்க
dy = ( e^{x2 – 5x + 7} (-sin (x² – 1)(2x)) + cos (x² – 1) e^{x2 – 5x + 7} (2x -5))dx
= e^{x2 – 5x + 7} [(2x – 5) cos (x² – 1) – 2x sin (x² -1)]dx

கேள்வி 2.
f(x)= x + 3x என்ற சார்பிற்கு ரி காண்க மற்றும்
(i) x = 2, dx = 0.1
(ii) x = 3 மற்றும் dx = 0.02 எனும் போது df -ஐ மதிப்பிடுக.
தீர்வு:
(i) x= 2, dx = 0.1
வகையீடு எடுக்க
df = (2x + 3) dx
x = 2 எனில், dx = 0.1
df = (2(2) + 3) (0.1)
= 7(0.1) = 0.7

(ii) x= 3 மற்றும் dx = 0.02
x = 3 எனில் dr = 0.02,
df = (6+ 3) (0.02)
= 9(0.02)
= 0.18

கேள்வி 3.
f என்ற சார்பிற்கு கொடுக்கப்பட்ட x, ∆x மதிப்புகளுக்கு ∆f மற்றும் df காண்க. மேலும் அவற்றை ஒப்பிடுக.
(i) f(x) = x³ – 2x²; x = 2, ∆x = dx= 0.5
(ii) f(x) = x² + 2x + 3; x=-0.5, ∆x = dx = 0.1
தீர்வு:
(i) f(x) = x³ – 2x²; x = 2, ∆x = dx = 0.5
கொடுக்கப்பட்ட f(x) = x³ – 2x²; x = 2, ∆x = d =0.5
df = f'(x).∆x = (3x² – 4x) ∆R
= [3(2)² – 4(2)] (0.5)
= 4(0.5) = 2.0

∆f = f (x + ∆x) – f(x)
= f(2.5) – f (2)
= [(2.5)³ – 2 (2.5)²] – [2³ – 2(2²)]
= 15.625 – 12.5 – 0 = 3.125

(ii) f(x) = x² + 2x + 3; x =-0.5, ∆x = dx = 0.1
df = f'(x) ∆r = (2x+ 2) (∆x)
x = -0.5, ∆x = dx = 0.1
df = (2(-0.5) + 2)0.1 = 0.1
∆f = f (x + ∆x) – f(x)
= f (-0.5 +0.1) – f (-0.5)
= f (-0.4) – f (-0.5)
= [(-0.4)² + 2 (-0.4) + 3] – [[-0.5)² + 2 (-0.5) + 3]
= (0.16 – 0.8 + 3) – (0.25 – 1 + 3)
= 2.36 – 2.25 = 0.11

கேள்வி 4.
log₁₀e = 0.4343 எனக்கொண்டு log₁₀1003-ன் தோராய மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட log₁₀e = 0.4343
கண்டுபிடிக்க வேண்டியது log₁₀1003
f(x) = log₁₀x, x₀ = 1000, dx = 3
f(1000) = log₁₀¹⁰⁰⁰
= log₁₀¹⁰³ = 3 log₁₀¹⁰
= 3(1) = 3
f'(x) = \(\frac{1}{x}\) log₁₀^e
f'(1000) = \(\frac{1}{1000}\) log₁₀^e
= \(\frac{1}{1000}\) (0.4343)
∴ L(x) = f(x) + f”(x) (x – x₀)
= 3 + \(\frac{1}{1000}\) (0.4343) (3)
= 3 + \(\frac{1.3029}{1000}\)
= 3 +0.0013029
log₁₀¹⁰⁰³ = 3.0013029

கேள்வி 5.
ஒரு மரத்தின் அடிப்பகுதியின் விட்டம் 30 செ.மீ. அடுத்த ஆண்டு அதன் சுற்றளவு 6 செ.மீ அதிகரிக்கின்றது எனில்
(i) தோராயமாக மரத்தின் விட்டம் எவ்வளவு வளர்ந்துள்ளது?
(ii) அதன் குறுக்கு வெட்டுப் பரப்பானது எவ்வளவு சதவீதம் அதிகரித்திருக்கும்?
தீர்வு:
(i) மூலை விட்டம் = 30 செ.மீ
ஆரம் = 15 செ.மீ
சுற்றளவு (c) = 2πr
= 2π(3) = 6π செ.மீ
dc = 2πdr
6 செ.மீ = 2πdr
\(\frac{6}{2 \pi}\) செ.மீ = dr
\(\frac{3}{\pi}\) செ.மீ = dr
மூலைவிட்டத்தின் தோராயமான வளர்ச்சி
2dr = 2 × \(\frac{3}{\pi}\) செ.மீ
= \(\frac{6}{\pi}\) செ.மீ

(ii) A = πr²
dA = π2r dr
dA = π 2 (15) \(\frac{3}{\pi}\) செ.மீ.
dA = 90 செ.மீ
பரப்பளவு = πr²
= π × 15 × 15 செ.மீ²
அதிகரிக்கும் சதவீதம் = \(\frac{90}{\pi \times 15 \times 15} \times 100=\frac{40}{\pi} \%\)

கேள்வி 6.
ஒரு குறிப்பிட்ட பறவையின் முட்டை கிட்டத்தட்ட கோள வடிவமாக உள்ளது. முட்டையின் ஆரம் ஓட்டிற்கு உள்ளே 5 மி.மீ ஆகவும் ஒட்டிற்கு வெளியே 5.3 மி.மீ ஆகவும் உள்ளது எனில் ஓட்டின் தோராய கன அளவைக் காண்க.
தீர்வு:
கோளத்தின் கன அளவு = \(\frac{4}{3}\) πr³
⇒ கொடுக்கப்பட்ட r = 5 மி.மீ
dr = (5.3 – 5) = 0.3 மி.மீ
தோராய கன அளவு = \(\frac{4}{3}\) π. 3r² dr
= 4π (5²)(0.3)
= 1001 (0.3)
= 30π மி.மீ³

கேள்வி 7.
மனிதனின் இரத்தக் குழாயின் (தமனியின்) குறுக்கு வெட்டானது வட்ட வடிவம் எனக் கொள்க. ஒரு நோயாளிக்கு இரத்தக் குழாய் விரிவடைவதற்கான மருந்து கொடுக்கப்பட்டுள்ளது. இரத்தக் குழாயின் ஆரம் 2 மி.மீ இலிருந்து 2.1 மி.மீ ஆக அதிகரிக்கும் போது அதன் குறுக்கு வெட்டின் பரப்பு தோராயமாக எந்த அளவு அதிகரிக்கும்? !
தீர்வு:
கொடுக்கப்பட்ட r = 2 மி.மீ
dr = (2.1 – 2) = 0.1 மி.மீ
பரப்பளவு = πr²
தோராயமான பரப்பு dA = 2πrdr
= 2π (2) (0.1)
= 4π (0.1) = 0.4 π மி.மீ.²

கேள்வி 8.
புதிதாக உருவாக்கப்பட்ட ஒரு நகரத்தின் வாக்காளர்களின் எண்ணிக்கையின் (ஆயிரங்களில்) அதிகரிப்பு V(t) = 30 + 12t² – t³, 0 ≤ t ≤ 8 என்பதால் மதிப்பிடப்படுகின்றது. இங்கு t என்பது ஆண்டுகளை குறிக்கின்றது. காலம் 4-இலிருந்து 4\(\frac{1}{6}\) வருடமாக இருக்கும் போது ஏற்படும் தோராய வாக்காளர்களின் எண்ணிக்கை மாற்றத்தைக் காண்க.
தீர்வு:
V(I) = 30 + 12t² – t³, 0 ≤ t ≤ 8
கொடுக்கப்பட்ட t = 4, dt = 4 \(\frac{1}{6}\) – 4 = 1
தோராயமாக வாக்காளர்களின் எண்ணிக்கை மாற்றம்
= (24t – 3t²) dt
= [24(4)- 3(4)²]\(\frac{1}{6}\)
= (96 – 48)\(\frac{1}{6}\) = \(\frac{48}{6}\) = 3
தோராயமாக வாக்காளர்களின் எண்ணிக்கை மாற்றம் = 8000.

கேள்வி 9.
ஒரு மனிதன் : மணி நேரத்தில் கற்கும் வார்த்தைகளுக்கான தொடர்பு ) = 52\(\sqrt{x}\), 0 ≤ x ≤ 9 எனக் கொடுக்கப்பட்டுள்ளது. x -ன் மதிப்பு பின்வருமாறு மாறும் போது கற்றல் வார்த்தைகளின் எண்ணிக்கையில் ஏற்படும் தோராய மாற்றத்தைக் காண்க.
(i) 1 இலிருந்து 1.1 மணி?
(ii) 4 இலிருந்து 4.1 மணி?
தீர்வு:
y = 52\(\sqrt{x}\), 0 ≤ x ≤ 9
(i) கொடுக்கப்பட்ட x = 1, dx = 1.1 – 1 = 0.1
தோராயமாக கற்ற வார்த்தைகளின் எண்ணிக்கை
= \(52 \cdot \frac{1}{2} x^{\frac{1}{2}-1}=\frac{26}{\sqrt{x}} d x\)
= \(\frac{26}{\sqrt{1}}\) (0.1) = 2.6
≅ 3 வார்த்தைகள்

(ii) x = 4 எனில், dx = 4.1 – 4 = 0.1
தோராயமாக கற்ற வார்த்தைகளின் எண்ணிக்கை
\(=\frac{26}{\sqrt{x}} d x=\frac{26}{\sqrt{4}}(0.1)=\frac{26}{2}(0.1)\)
= 13(0.1) = 1.3
≅ 1 வார்த்தை .

கேள்வி 10.
ஒரு வட்ட வடிவத் தகடு வெப்பத்தினால் சீராக விரிவடைகின்றது என்க. அதன் ஆரம் 10.5 செ.மீ – இலிருந்து 10.75 செ.மீ – ஆக அதிகரிக்கும் போது அதன் பரப்பில் ஏற்படும் தோராய அதிகரிப்பு மற்றும் தோராய சதவீத அதிகரிப்பு ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட r = 10.5 செ.மீ
dr = 10.75 – 10.5 = 0.25
பரப்பு = πr²
பரப்பில் ஏற்படும் தோராய மாற்றம் = π (2r) dr
= 2π (10.5) (0.25)
= 5.251 செ.மீ²
பரப்பில் ஏற்படும் தோராய சதவீத மாற்றம்
= \(\frac{5.25 \pi}{\pi(10.5)(10.5)} \times 100\)
= \(\frac{5.25}{110.25} \times 100\)
= 0.0476 × 100 = 4.76%

கேள்வி 11.
10 செ.மீ பக்க அளவு கொண்ட ஒரு கன சதுரத்தின் பக்கங்களுக்கு 0.2 செ.மீ கனத்திற்கு வர்ணம் பூசப்படுகின்றது. வகையீடுகளைப் பயன்படுத்தி அந்த கன சதுரத்தின் வர்ணப்! பூச்சிற்கு தோராயமாக எத்தனை கன செ.மீ அளவிற்கு வர்ணம் பயன்படுத்தப்பட்டது எனக் காண்க . மேலும் துல்லியமாக எவ்வளவு வர்ணம் பயன்படுத்தப்பட்டது என்பதையும் காண்க.
தீர்வு:
கொடுக்கப்பட்ட a = கன சதுரத்தின் பக்க அளவு |
= 10 செ.மீ மற்றும்
dx = 0.2 செ.மீ
கன சதுரத்தின் கன அளவு = a³
தோராயமாக பயன்படுத்தப்பட்ட வர்ணத்தின் கன
செ.மீ அளவு = 3a² da
= 3(10²) (0.2)
= 300\(\left(\frac{2}{10}\right)\) = 60 செ.மீ³
துல்லியமாக பயன்படுத்தப்பட்ட வர்ணத்தின் அளவு
= f (x + ∆x) – f (x)
= f (10.2) – f (10)
= 10.2³ – 10³
= 1061.208 – 1000
= 61.208 செ.மீ³