Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.10 Textbook Questions and Answers, Notes.
TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.10
சரியான அல்லது மிகப் பொருத்தமான விடையினை தேர்ந்தெடுத்து எழுதுக :
கேள்வி 1.
ஒரு கோளத்தின் கன அளவு வினாடிக்கு 3π செ.மீ3 வீதத்தில் அதிகரிக்கிறது. ஆரம் \(\frac{1}{2}\) செ.மீ ஆக இருக்கும் போது ஆரத்தின் மாறுபட்டு வீதம்
(1) 3 செ.மீ/வி
(2) 2 செ.மீ/வி
(3) 1 செ.மீ/வி
(4) \(\frac{1}{2}\) செ.மீ/வி
விடை:
(1) 3 செ.மீ/வி
குறிப்பு:

![]()
கேள்வி 2.
ஒரு பலூனானது செங்குத்தாக மேல் நோக்கி 10 மீ/வி வீதத்தில் செல்கிறது. பலூன் செலுத்தப்பட்ட இடத்திலிருந்து 40மீ தொலைவில் இடமிருந்து ஒருவர் இதனைப் பார்க்கிறார். பலூனின் ஏற்றக் கோணத்தில் ஏற்படும் மாறுபாட்டு வீதத்தை பலூன் தரையிலிருந்து 30 மீட்டர் உயரத்தில் இருக்கும் போது காண்க.
(1) \(\frac{3}{25}\) ரேடியன்கள்/ வினாடி
(2) \(\frac{4}{25}\) ரேடியன்கள்/ வினாடி
(3) \(\frac{1}{5}\) ரேடியன்கள்/ வினாடி
(4) \(\frac{1}{3}\) ரேடியன்கள்/ வினாடி
விடை:
(2) \(\frac{4}{25}\) ரேடியன்கள்/ வினாடி
குறிப்பு:
tan θ = \(\frac{h}{40}\)

கேள்வி 3.
t என்ற காலத்தில் கிடைமட்டமாக நகரும் துகளின் நிலை s(t) = 3t2 -2t — 8 எனக் கொடுக்கப்பட்டுள்ளது. துகள் ஓய்வு நிலைக்கு வரும் நேரம்
(1) t = 0
(2) t = \(\frac{1}{3}\),
(3) t = 1
(4) t = 3
விடை:
(2) t = \(\frac{1}{3}\)
குறிப்பு:
S(t) = 3t2 – 2t – 8
\(\frac{d s}{d t}\) = 6t – 2
⇒ \(\frac{d s}{d t}\) = 0
⇒ 6t – 2 = 0
⇒ t = \(\frac{1}{3}\)
![]()
கேள்வி 4.
ஒரு கல்லானது செங்குத்தாக மேல்நோக்கி எறியப்படுகின்றது. t நேரத்தில் அது அடைந்த உயரம் x = 80t – 16t2. கல் அதிகபட்ச உயரத்தை t வினாடி நேரத்தில் அடைந்தால் t ஆனது
(1) 2
(2) 2.5
(3) 3
(4) 3.5
விடை:
(2) 2.5
குறிப்பு:
x = 80t – 16t2
\(\frac{d x}{d t}\) = 80 – 32 t
\(\frac{d x}{d t}\) = 0
⇒ 80 – 32t = 0
⇒ t = \(\frac{80}{32}=\frac{10}{4}=\frac{5}{2}\) = 2.5 வினாடி
கேள்வி 5.
6y = x3 + 2 என்ற வளைவரையின் எப்புள்ளியில் y-ஆயத்தொலைவின் மாறுபாட்டு வீதம் x-ஆய்த்தொலைவின் மாறுபாட்டு வீதத்தைப் போல் 8 மடங்கு இருக்கும்.
(1) (4, 11)
(2) (4, -11)
(3) (-4, 11)
(4) (-4, -11)
விடை:
(1) (4, 11)
குறிப்பு:
கொடுக்கப்பட்ட \(\frac{d y}{d t}=8 \frac{d x}{d t}\)
6y = x3 + 2
⇒ 6\(\frac{d y}{d t}\) = 3x2 \(\frac{d x}{d t}\)
⇒ \(6\left(8 \frac{d x}{d t}\right)=3 x^{2}\left(\frac{d x}{d t}\right)\)
⇒ x2 = 16
⇒ x = ±4
x = 4 எனில், 6y = 64 + 2 = 66 ⇒ y = 11
![]()
கேள்வி 6.
f(x) = \(\sqrt{8-2 x}\) என்ற வளைவரையின் எந்த x – ஆயத்தொலைவில் வரையப்பட்ட தொடு கோட்டின் சாய்வு -0.25 இருக்கும்?
(1) -8
(2) -4
(3) -2
(4) 0
விடை:
(2) -4
குறிப்பு: _
f(x) = \(\sqrt{8-2 x}\)
f'(x) = \(\frac{-1}{\sqrt{8-2 x}}\)
∴ \(\frac{-1}{\sqrt{8-2 x}}\) = -0.25
⇒ \(\frac{1}{8-2 x}\) = 0.0625
⇒ 8 – 2x = \(\frac{1}{0.0625}\)
⇒ 8 – 2x = 16
⇒ 2x = -8
⇒ x = -4
கேள்வி 7.
f(x) = 2cos 4x என்ற வளைவரைக்கு x = \(\frac{\pi}{12}\) செங்கோட்டின் சாய்வு
(1) -4\(\sqrt{3}\)
(2) -4
(3) \(\frac{\sqrt{3}}{12}\)
(4) 4\(\sqrt{3}\)
விடை:
(3) \(\frac{\sqrt{3}}{12}\)
குறிப்பு:
f(x) = 2 cos 4x
⇒ f'(x) = -8 sin 4x
x = \(\frac{\pi}{12}\) -ல் செங்குத்தின் சாய்வு
= \(\frac{1}{8 \sin 4 x}=\frac{1}{8 \sin 4 \times \frac{\pi}{12}}=\frac{1}{8 \sin \frac{\pi}{3}}\)
= \(\frac{1}{8 \frac{\sqrt{3}}{2}}=\frac{1}{4 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{12}\)
![]()
கேள்வி 8.
y2 – xy + 9 = 0 என்ற வளைவரையின் தொடு கோடு எப்போது நிலைகுத்தாக இருக்கும்?
(1) y = 0
(2) y = ± \(\sqrt{3}\)
(3) y = \(\frac{1}{2}\)
(4) y = ± 3
விடை:
(4) y = ± 3
குறிப்பு:
y2 – xy + 9 = 0 …….. (1)
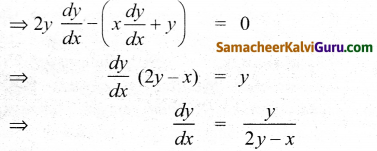
தொடுகோடு செங்குத்து எனில் θ = 90°
⇒ tan θ = ∞
⇒ \(\frac{d y}{d x}\) = ∞
⇒ 2y – x = 0
⇒ 2y = x
∴ (1) லிருந்து y – 2y2 + 9 = 0
⇒ -y2 = -9
⇒ y2 = 9
⇒ y = ±3
கேள்வி 9.
ஆதியில் y2= x மற்றும் x2 = y என்ற வளைவரைகளுக்கு இடைப்பட்ட கோணம்
(1) \(\tan ^{-1} \frac{3}{4}\)
(2) \(\tan ^{-1}\left(\frac{4}{3}\right)\)
(3) \(\frac{\pi}{2}\)
(4) \(\frac{\pi}{4}\)
விடை:
(3) \(\frac{\pi}{2}\)
குறிப்பு:
y2 = x …. (1)
⇒ 2y \(\frac{d y}{d x}\) = 1
⇒ \(\frac{d y}{d x}\) = \(\frac{1}{2y}\)
⇒ m1 = \(\left(\frac{d y}{d x}\right)_{(0,0)}=\frac{1}{0}\) = ∞
θ = \(\frac{\pi}{2}\)
x2 = y
⇒ 2x = \(\frac{d y}{d x}\)
⇒ m2 = 2(0) = 0
∴ θ = 0 [∵ tan θ = tan \(\frac{\pi}{2}\) = ∞]
![]()
கேள்வி 10.
\(\lim _{x \rightarrow 0}\left(\cot x-\frac{1}{x}\right)\) -ன் மதிப்பு
(1) 0
(2) 1
(3) 2
(4) ∞
விடை:
(4) ∞
கேள்வி 11.
sin4x + cos4x என்ற சார்பு இறங்கும் இடைவெளி
(1) \(\left[\frac{5 \pi}{8}, \frac{3 \pi}{4}\right]\)
(2) \(\left[\frac{\pi}{2}, \frac{5 \pi}{8}\right]\)
(3) \(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)
(4) \(\left[0, \frac{\pi}{4}\right]\)
விடை:
(3) \(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)
குறிப்பு:
sin4x + cos4x = f (x)
⇒ f'(x) = 4 sin3x cos x – 4 cos3x sinx
⇒ f'(x) = 4 sin x cos x (sin2x – cos2x)
= -2 sin 2x (cos 2 x)
f'(x) = -4 cos 4x
\(\left(\frac{\pi}{4}, \frac{\pi}{2}\right)\) இல் x = \(\frac{\pi}{3}\) என்க, f'(x) = -4 cos 4\(\frac{\pi}{3}\)
= -4 cos\(\left(\pi+\frac{\pi}{3}\right)\)
f'(x) = \(-4\left(-\cos \frac{\pi}{3}\right)\)
= \(4 \cos \frac{\pi}{3}=4\left(\frac{1}{2}\right)\)
= 2 = +ve
∴ sin4x + cos4x \(\left(\frac{\pi}{4}, \frac{\pi}{2}\right)\) -ல் இறங்கும் என்க.
![]()
கேள்வி 12.
x3 – 3x2, x ∈ [0, 3] என்ற சார்பிற்கு ரோலின் தேற்றத்தை நிறைவு செய்யும் எண்
(1) 1
(2) \(\sqrt{2}\)
(3) \(\frac{3}{2}\)
(4) 2
விடை:
(4) 2
குறிப்பு:
f(x) = x3 – 3x2,
⇒ f'(x) = 3x2 – 6x,
c எனும் எண் பின்வருமாறு உள்ளதெனில்
3c2 – 6c = 0
3c (c – 2) = 0
⇒ c = 0 அல்லது c = 2
கேள்வி 13.
\(\frac{1}{x}\), x ∈ [1, 9] என்ற சார்பிற்கு சராசரி மதிப்புத் தேற்றத்தை நிறைவு செய்யும் எண்
(1) 2
(2) 2.5
(3) 3
(4) 3.5
விடை:
(3) 3
குறிப்பு:

கேள்வி 14.
|3 – x| + 9 என்ற சார்பின் குறைந்த மதிப்பு
(1) 0
(2) 3
(3) 6
(4) 9
விடை:
(4) 9
குறிப்பு:
f(x) = |3 – x| + 9
⇒ |3 – x| ≥ 0 x ∈ R
⇒ |3 – x| – ன் குறைந்த மதிப்பு 0
∴ f(x) = 0 + 9 = 9 -ன் குறைந்த மதிப்பு
![]()
கேள்வி 15.
y = ex sin x, x ∈ [0, 2π] என்ற வளைவரையின் மீப்பெரு சாய்வு எங்கு அமையும்?
(1) x = \(\frac{\pi}{4}\)
(2) x = \(\frac{\pi}{2}\)
(3) x = π
(4) x = \(\frac{3\pi}{2}\)
விடை:
(2) x = \(\frac{\pi}{2}\)
குறிப்பு:
\(\frac{d y}{d x}\) ex (sin x + cos x)
\(\frac{d^{2} y}{d x^{2}}\) = ex (sin x + cos x) + ex(cos x – sin x)
= 2ex cos x
\(\frac{d^{2} y}{d x^{2}}\) = 0
x = \(\frac{\pi}{2}\)
கேள்வி 16.
x2e-2x, x > 0 என்ற சார்பின் பெரும் மதிப்பு
(1) \(\frac{1}{e}\)
(2) \(\frac{1}{2e}\)
(3) \(\frac{1}{e^{2}}\)
(4) \(\frac{4}{e^{4}}\)
விடை:
(3) \(\frac{1}{e^{2}}\)
குறிப்பு:
f(x) = x2e-2x
f'(x) = 2e-2x (- x2 + x)
f'(x) = 0
⇒ x = 0, 1
f”(x) = 2e-2x (- 2x2 + 1)
x = 1 எனில், f”(1) = 2-2 (-1) < 0
∴ x = 1 f (x) -ன் பெருமம் ஆகும்
∴ f(1) = 12 e-2 = \(\frac{1}{e^{2}}\)
![]()
கேள்வி 17.
(6, 0) என்ற புள்ளிக்கும் x2 – y2 = 4 என்ற வளைவரை மீதுள்ள புள்ளிக்கும் உள்ள தொலைவு குறைந்தபட்சம் எனில் அப்புள்ளி
(1) (2, 0)
(2) (\(\sqrt{5}\), 1)
(3) (3, \(\sqrt{5}\))
(4) (\(\sqrt{13}\), –\(\sqrt{3}\))
விடை:
(3) (3, \(\sqrt{5}\))
குறிப்பு:
h2 – k2 = 4

கேள்வி 18.
இரண்டு மிகை எண்களின் கூடுதல் 200 மேலும் அவற்றின் பெருக்கல் பலனின் பெரும மதிப்பு.
(1) 100
(2) 25\(\sqrt{7}\)
(3) 28
(4) 24\(\sqrt{14}\)
விடை:
(1) 100
குறிப்பு:
x2 + y2 = 200
⇒ y2 = 200 – x2
f (x) = xy
= x\(\sqrt{200-x^{2}}\)
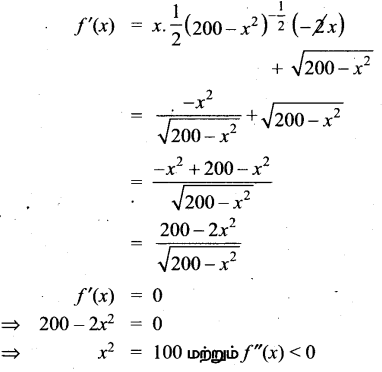
![]()
கேள்வி 19.
y = ax4 + bx2, ab > 0 என்ற வளைவரை
(1) கிடைமட்டத் தொடுகோடு பெறவில்லை
(2) மேற்புறமாக குழிவு
(3) கீழ்புறமாக குழிவு
(4) வளைவு மாற்றுப் புள்ளியை பெறவில்லை
விடை:
(4) வளைவுமாற்றுப்புள்ளியை பெறவில்லை
குறிப்பு:
y = ax4 + bx2
\(\frac{d y}{d x}\) = 4ax3 + 2bx|
\(\frac{d^{2} y}{d x^{2}}\) = 12ax2 + 26
⇒ 12ax2 = – 2b
⇒ x2 = \(\)
⇒ x = கற்பனை எண்
\(\frac{d^{3} y}{d x^{3}}\) = 24ax
![]()
கேள்வி 20.
y = (x – 1)3 என்ற வளைவரையின் வளைவு மாற்றுப் புள்ளி
(1) (0, 0)
(2) (0, 1)
(3) (1, 0)
(4) (1, 1)
விடை:
(3) (1, 0)
குறிப்பு:
y = (x – 1)3
\(\frac{d y}{d x}\) = 3(x- 1)2
\(\frac{d^{2} y}{d x^{2}}\) = 6 (x – 1) = 0
⇒ x = 1
\(\frac{d^{3} y}{d x^{3}}\) = 6 |
x = 1 எனில், \(\frac{d^{3} y}{d x^{3}}\) = 6 ≠ 0
வளைவு மாற்றுப் புள்ளி (1, f (1))
f(1) = (1 – 1)3 = 0