Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.9

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.9 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.9

கேள்வி 1.
\(\vec{r} \cdot(2 \hat{i}-7 \hat{j}+4 \hat{k})=3\) மற்றும் 3x – 5y + 4z + 11 = 0, என்ற தளங்களின் வெட்டுக்கோடு வழியாகவும் (-2, 1, 3) என்ற புள்ளி வழியாகவும் செல்லும் தளத்தின் சமன்பாடு காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளங்களின் சமன்பாடு
\(\vec{r} \cdot(2 \hat{i}-7 \hat{j}+4 \hat{k})=3\) மற்றும் 3x – 5y + 4z +11 = 0.
தளங்களின் வெட்டுக்கோட்டின் வழிச்செல்லும் தளத்தின் வெக்டர் சமன்பாடானது \(\vec{r} \cdot \vec{n}_{1}=d_{1}\) மற்றும் \(\vec{r} \cdot \vec{n}_{2}=d_{2}\)
\(\left(\vec{r} \cdot \vec{n}_{1}-d_{1}\right)+\lambda\left(\vec{r} \cdot \vec{n}_{2}-d_{2}\right)=0\) ………….. (1)
\(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) பிரதியிட
\(\vec{n}_{1}=2 \hat{i}-7 \hat{j}+4 \hat{k}, \vec{n}_{2}=3 \hat{i}-5 \hat{j}+4 \hat{k}\)
d₁ = +3, d₂ = -11 என (1) ல் பிரதியிட கிடைப்பது,
\([(x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}-7 \hat{j}+4 \hat{k}-3)]\) + \(\lambda[(x \hat{i}+y \hat{j}+z \hat{k}) \cdot(3 \hat{i}-5 \hat{j}+4 \hat{k})+11]\) = 0
⇒ (2x – 7y + 4z – 3) + λ (3x – 5y + 4z + 11) = 0 ………….. (2)
புள்ளி (-2, 1, 3) வழி தளம் செல்வதால் கிடைப்பது,
[2(-2) – 7(1) + 4(3) – 3] + 2 [-6 – 5 + 12 + 11] = 0
⇒ (-4 – 7 + 12 – 3) + λ (12) = 0
⇒ -2 + 12λ = 0 ⇒ 12λ = 2 ⇒ λ = \(\frac{1}{6}\)
λ = \(\frac{1}{6}\) என (1)ல் பிரதியிட கிடைப்பது,
(2x-7y +4z – 3) + \(\frac{1}{6}\) (3x – 5y + 4z + 11) = 0
6 ஆல் பெருக்க கிடைப்பது,
⇒ 12x – 42y + 24z – 18 + 3x – 5y + 4z + 11 = 0
⇒ 15x – 47y + 28z – 7 = 0 என்பது தேவையான தளத்தின் சமன்பாடு

கேள்வி 2.
x+2y + 3z = 2 மற்றும் x – y + z +11 = 3 என்ற தளங்களின் வெட்டுக்கோடு வழிச்செல்வதும், (3, 1, -1) என்ற புள்ளியிலிருந்து \(\frac{2}{\sqrt{3}}\) தொலைவில் உள்ளதுமான தளத்தின் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளங்களின் சமன்பாடுகள்
x + 2y + 3z = 2 மற்றும் x – y + z + 11 = 3
தளங்களின் வெட்டுக்கோட்டின் வழிச் செல்லும் தளத்தின் கார்டீசியன் வடிவம்
(a₁x + b₁y + c₁ z – d₁) + 2 (a₂x + b₂y + c₂z – d₂) = 0
∴ தேவையான தளத்தின் சமன்பாடு
(x + 2y + 3z – 2) + λ (x + y + z + 8) = 0 (1)
x(λ + 1) + y(2 + λ) + z(3 + λ) — 2 + 8λ = 0
(3, 1, -1) மற்றும் தளத்திற்கு இடையேயான தூரம் \(\frac{2}{\sqrt{3}}\)

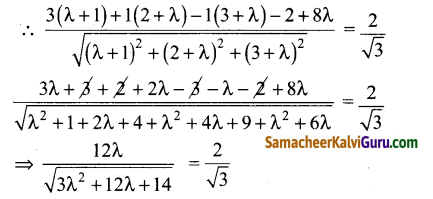
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது
⇒ \(\frac{144 \lambda^{2}}{3 \lambda^{2}+12 \lambda+14}=\frac{4}{3}\)
⇒ 432λ² = 12λ² + 48λ + 56
⇒ 420λ² – 48λ – 56 = 0 ÷ 2
⇒ 210λ² – 24λ – 28 = 0
⇒ 105λ² – 12λ – 14 = 0
1-ன் மதிப்பு காண, சமன்பாட்டை தீர்க்க. ஆனால் இந்த சமன்பாட்டிற்கு விகிதமுறா மூலங்கள் உள்ளன.

கேள்வி 3.
\(\overrightarrow{\boldsymbol{r}}=(2 \hat{\boldsymbol{i}}-\hat{\boldsymbol{j}}+\hat{\boldsymbol{k}})+t(\hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}-2 \hat{\boldsymbol{k}})\) என்ற கோட்டிற்கும் \(\vec{r} \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})\) = 8 என்ற தளத்திற்கும் இடைப்பட்ட கோணம் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளத்தின் சமன்பாடு
\(\vec{r} \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})\) = 8
∴ \(\vec{n}_{1}=6 \hat{i}+3 \hat{j}+2 \hat{k}\) மற்றும் அந்த கோடு
\(\overrightarrow{\boldsymbol{r}}=(2 \hat{\boldsymbol{i}}-\hat{\boldsymbol{j}}+\hat{\boldsymbol{k}})+t(\hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}-2 \hat{\boldsymbol{k}})\)
∴ \(\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}\)
தளம் மற்றும் கோட்டிற்கும் இடையேயான கோணம்

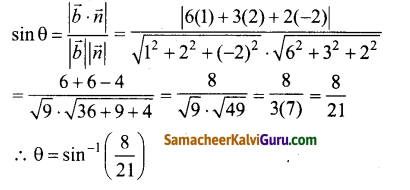
கேள்வி 4.
\(\vec{r} \cdot(\hat{i}+\hat{j}-2 \hat{k})\) = 3 மற்றும் 2x – 2y + z = 2 என்ற தளங்களுக்கு இடைப்பட்ட கோணம் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளங்கள் \(\vec{r} \cdot(\hat{i}+\hat{j}-2 \hat{k})\) = 3
மற்றும் 2x – 2y + z = 2 ⇒ \(\vec{r} \cdot(2 \hat{i}-2 \hat{j}+\hat{k})\) = 2
∴ \(\vec{n}_{1}=\hat{i}+\hat{j}-2 \hat{k}\) மற்றும் \(\vec{n}_{2}=2 \hat{i}-2 \hat{j}+\hat{k}\)
தளங்களுக்கு இடையேயான கோணம்

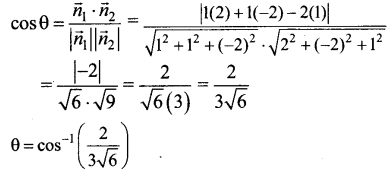
கேள்வி 5.
(3, 4, -1) என்ற புள்ளி வழிச் செல்வதும் 2x – 3y + 5z + 7 = 0 என்ற தளத்திற்கு இணை யானதுமான தளத்தின் சமன்பாட்டைக் காண்க. மேலும், இவ்விரு தளங்களுக்க இடைப்பட்ட தொலைவினைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளத்தின் சமன்பாடு
2x – 3y + 5z + 7 = 0
கொடுக்கப்பட்ட தளத்திற்கு இணையான தளத்தின்
சமன்பாடு 2x – 3y + 5z + k =0 …………..(1)
புள்ளி (3,4,-1) வழி தளம் செல்வதால் கிடைப்பது
2(3) – 3(4) + 5(-1) + k = 0
⇒ 6- 12 – 5 + k = 0
⇒ -11 + k = 0 ⇒ k = 11
∴ (1) லிருந்து, 2x – 3y + 5z + 11 = 0 என்பது! தேவையான தளத்தின் சமன்பாடு
இண்டு இணை தளங்களுக்கு இடையேயான
தூரம் = \(\frac{\left|d_{1}-d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
∴ d = \(\frac{|7-11|}{\sqrt{2^{2}+(-3)^{2}+5^{2}}}=\frac{|-4|}{\sqrt{4+9+25}}\)
= \(\frac{4}{\sqrt{38}}\) அலகுகள்

கேள்வி 6.
(1,-2, 3) என்ற புள்ளியிலிருந்து x – y + z = 5 என்ற தளத்திற்கு வரையப்பட்ட செங்குத்தின் நீளம் காண்க.
தீர்வு:
(x, y, z,) லிருந்து தளம் ax + by + cz – p = 0 க்கான
செங்குத்தின் நீளம் \(\left|\frac{a x_{1}+b y_{1}+c z_{1}-p}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)
∴ (1, -2, 3) லிருந்து தளத்துக்கான செங்குத்தின் நீளம்
x – y + z – 5 = 0. δ = \(\left|\frac{1-(-2)+3-5}{\sqrt{1^{2}+(-1)^{2}+1^{2}}}\right|\)
= \(\left|\frac{1+2+3-5}{\sqrt{1+1+1}}\right|=\left|\frac{1}{\sqrt{3}}\right|\)
= \(\frac{1}{\sqrt{3}}\) அலகுகள்

கேள்வி 7.
x – 1 = \(\), = z + 1 என்ற கோடும் 2x – y + 2z = 2 என்ற தளமும் சந்திக்கும் புள்ளியைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோட்டின் சமன்பாடு
\(\frac{x-1}{1}=\frac{y}{2}\) = z + 1 = s
⇒ x – 1 = s ⇒ x = s +1
\(\) = s ⇒ y = 2s
z + 1 = s ⇒ z = s – 1
∴ கோட்டிலுள்ள ஏதேனும் ஒரு புள்ளியின் வடிவம் (s + 1, 2s, s – 1)
இந்த புள்ளியானது 2x – y + 2z = 2 தளத்தில் அமைந்துள்ளது.
⇒ 2(s + 1) – (2s) + 2(s – 1) = 2
⇒ 2s + 2 – 2s + 26 -2 = 2
⇒ 2s = 2 ⇒ s = 1
s = 1, எனில் புள்ளியானது (1 + 1, 2(1), 1 – 1) = (2, 2, 0)
என்பது தளம் மற்றும் கோட்டின் வெட்டு புள்ளி

கேள்வி 8.
(4, 3, 2) என்ற புள்ளியில் இருந்து x + 2y + 3z = 2 என்ற தளத்திற்கு வரையப்படும் செங்குத்தின் அடியின் அச்சுத்தூரங்களையும், செங்குத்தின் நீளத்தையும் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளத்தின் சமன்பாடு
x + 2y + 3z = 2
(4, 3, 2) லிருந்து தளத்துக்கான செங்குத்தின் நீளம்
d = \(\frac{4+2(3)+3(2)}{\sqrt{1^{2}+2^{2}+3^{2}}}=\frac{4+6+6}{\sqrt{14}}\)
= \(\frac{14}{\sqrt{14}}=\frac{\sqrt{14} \cdot \sqrt{14}}{\sqrt{14}}=\sqrt{14}\) அலகுகள்
தளம் x + 2y + 3z = 2 யில் புள்ளி (4, 3, 2) க்கான பிம்பம் காண்போம்.
இங்கு \(\vec{u}=4 \hat{i}+3 \hat{j}+2 \hat{k}, \vec{n}=\hat{i}+2 \hat{j}+3 \hat{k}\) மற்றும் p = 38

= \(\frac{6 \hat{i}+2 \hat{j}-2 \hat{k}}{2}=3 \hat{i}+\hat{j}-\hat{k}\)
எனவே செங்குத்தின் அடிப்பகுதியின் ஆயத்தொலைவு (3, 1, -1)