Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.8 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.8

கேள்வி 1.
\(\vec{r}=(5 \hat{i}+7 \hat{j}-3 \hat{k})+s(4 \hat{i}+4 \hat{j}-5 \hat{k})\) மற்றும் \(\vec{r}=(8 \hat{i}+4 \hat{j}+5 \hat{k})+t(7 \hat{i}+\hat{j}+3 \hat{k})\) ஆகிய கோடுகள் ஒரே தளத்தில் அமையும் எனக் காண்பிக்க மேலும், இக்கோடுகள் அமையும் தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்
\(\vec{r}=(5 \hat{i}+7 \hat{j}-3 \hat{k})+s(4 \hat{i}+4 \hat{j}-5 \hat{k})\)
மற்றும் \(\vec{r}=(8 \hat{i}+4 \hat{j}+5 \hat{k})+t(7 \hat{i}+\hat{j}+3 \hat{k})\)
\(\vec{a}=5 \hat{i}+7 \hat{j}-3 \hat{k}, \vec{b}=4 \hat{i}+4 \hat{j}-5 \hat{k}\) என்க
\(\vec{c}=8 \hat{i}+4 \hat{j}+5 \hat{k}\) மற்றும் \(\vec{d}=7 \hat{i}+\hat{j}+3 \hat{k}\)
இரண்டு கோடுகள் ஒரு தளம் அமைவன எனில்

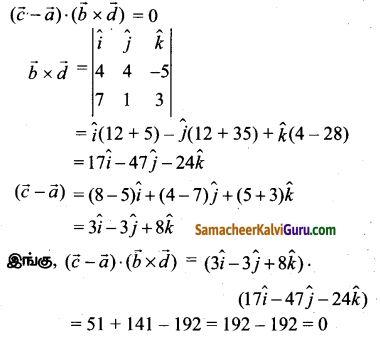
∴ கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமைவன. ஒரு தளம் அமையும் கோடுகளை கொண்ட தளம்.

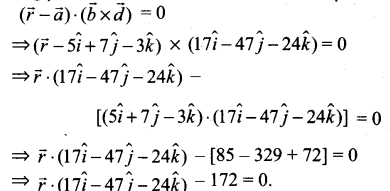
என்பது தேவையான வெக்டர் தளத்திற்கான சமன்பாடு

கேள்வி 2.
\(\frac{x-2}{2}=\frac{y-3}{1}=\frac{z-4}{3}\) மற்றும் \(\frac{x-1}{-3}=\frac{y-4}{2}=\frac{z-5}{1}\) என்ற கோடுகள் ஒரு தளத்தில் அமையும் எனக்காட்டுக. மேலும், இக்கோடுகள் அமையும் தளத்தினைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள் \(\frac{x-2}{2}=\frac{y-3}{1}=\frac{z-4}{3}\) மற்றும்

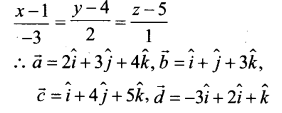
கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமைவன

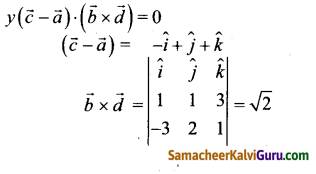
= \(\hat{i}(1-6)-\hat{j}(1+9)+\hat{k}(2+3)\)
= \(-5 \hat{i}-10 \hat{j}+5 \hat{k}\)
∴ \((\vec{c}-\vec{a}) \cdot(\vec{b} \times \vec{d})=(-\hat{i}+\hat{j}+\hat{k}) \cdot(-5 \hat{i}-10 \hat{j}+5 \hat{k})\)
= 5 – 10 + 5 = 10 – 10 = 0
எனவே கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமையும்.
அதனுடைய கார்டீசியன் சமன்பாடானது
\(\left|\begin{array}{ccc}
x-x_{2} & y-y_{2} & z-z_{2} \\
b_{1} & b_{2} & b_{3} \\
d_{1} & d_{2} & d_{3}
\end{array}\right|=0\)
⇒ \(\left|\begin{array}{ccc}
x-1 & y-4 & z-5 \\
1 & 1 & 3 \\
-3 & 2 & 1
\end{array}\right|=0\)
⇒ (x – 1) (1 – 6) – (y – 4) (1 + 9) + (z – 5) (2 + 3) =0
⇒ (x – 1) (- 5) – (y – 4) (10) + (z – 5) (5) = 0
⇒ -5x + 5 – 10y + 40 + 5z – 25 = 0
⇒ -5x – 10y + 5z + 20 = 0
÷ -5 கிடைப்பது,
x + 2y – z – 4 = 0 என்பது கொடுக்கப்பட்ட கோடுகள் கொண்ட தளத்தின் சமன்பாடு.

கேள்வி 3.
\(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{m^{2}}\) மற்றும் \(\frac{x-1}{1}=\frac{y-2}{m^{2}}=\frac{z-1}{2}\) ஆகிய கோடுகள் ஒரே தளத்தில் அமைகின்றன! எனில், m-ன் வேறுபட்ட மெய்மதிப்புகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள் \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{m^{2}}\)

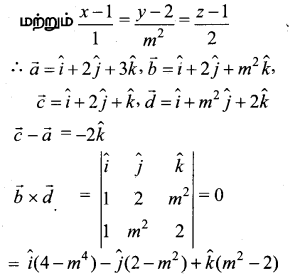
ஆகையால் கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமைவன,
\((\vec{c}-\vec{a}) \cdot(\vec{b} \times \vec{d})=0\)
⇒ \((-2 \hat{k}) \cdot\left[\left(4-\dot{m}^{4}\right) \hat{i}-\hat{j}\left(2-m^{2}\right)+\hat{k}\left(m^{2}-2\right)\right]=0\)
⇒ -2(m² – 2) = 0
⇒ m² – 2 = 0 [∵ -2 ≠ 0]
⇒ m² = 2
⇒ m = ±\(\sqrt{2}\)

கேள்வி 4.
\(\frac{x-1}{2}=\frac{y+1}{\lambda}=\frac{z}{2}\) மற்றும் \(\frac{x+1}{5}=\frac{y+1}{2}=\frac{z}{\lambda}\) ஆகிய கோடுகள் ஒரே தளத்தில் அமைகின்றன எனில், 2-ன் மதிப்பைக் காண்க. மேலும், இவ்விரு கோடுகளைக் கொண்ட தளங்களின் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்

கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமைவன ஆதலால்
\((\vec{c}-\vec{a}) \cdot(\vec{b} \times \vec{d})=0\)
⇒ \((-2 \vec{i}) \cdot\left[\left(\lambda^{2}-4\right) \hat{i}-\hat{j}(2 \lambda-10)+\hat{k}(4-5 \lambda)\right]=0\)
⇒ -2 (l² – 4) = 0
⇒ λ² = 4 [∵ -2 ≠ 0]
⇒ λ = ± \(\sqrt{4}\) = ±2
கொடுக்கப்பட்ட கோடுகளை கொண்டிருக்கும் தளத்தின் கார்டீசியம் சமன்பாடு
\(\left|\begin{array}{ccc}
x-x_{2} & y-y_{2} & z-z_{2} \\
b_{1} & b_{2} & b_{3} \\
d_{1} & d_{2} & d_{3}
\end{array}\right|=0\)
⇒ \(\left|\begin{array}{ccc}
x+1 & y+1 & z \\
2 & 2 & 2 \\
5 & 2 & 2
\end{array}\right|=0\) [∵λ = 2]
⇒ (x + 1) (4 – 4) – (y + 1) (4 – 10) + z (4 – 10) = 0
⇒ (x + 1) (0) – (y + 1) (-6) + z (-6) = 0
⇒ 6 (y + 1) – 6z = 0
⇒ y + 1 – z = 0 [÷6]
⇒ y – z + 1 = 0 என்பது கொடுக்கப்பட்ட கோடுகளை கொண்டிருக்கும் தேவையான தளத்தின் சமன்பாடு.