Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.2

கேள்வி 1.
\(\vec{a}\) = \(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) + 3\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = 2\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\), \(\vec{c}\) = 3\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + \(\hat{\boldsymbol{k}}\), எனில் \(\vec{a}\).(\(\vec{b}\) × \(\vec{c}\)) காண்க.
தீர்வு:
கொடுக்கப்பட்ட \(\vec{a}\) = \(\hat{\boldsymbol{i}}\) – 2\(\hat{\boldsymbol{j}}\) + 3\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = 2\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\), \(\vec{c}\) = 3\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) + \(\hat{\boldsymbol{k}}\)

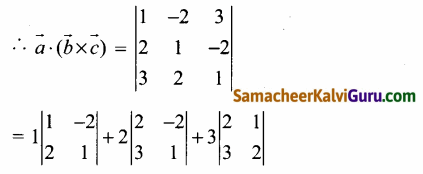
= 1 (1 + 4) + 2 (2 + 6) + 3 (4 – 3)
= 1(5) + 2(8) + 3(1) = 5 + 16 + 3 = 24
∴ \(\vec{a}\).(\(\vec{b}\) × \(\vec{c}\)) = 24 .

கேள்வி 2.
-6\(\hat{\boldsymbol{i}}\) + 14\(\hat{\boldsymbol{j}}\) + 10\(\hat{\boldsymbol{k}}\), 14\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) – 6\(\hat{\boldsymbol{k}}\) மற்றும் \(\vec{c}\) = 2\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\)
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) என்ற வெக்டர்களால் குறிப்பிடப்படும் ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளைக் கொண்ட இணைகரத் திண்மத்தின் கன அளவைக் காண்க.
தீர்வு:
\(\vec{a}\) = -6\(\hat{\boldsymbol{i}}\) + 14\(\hat{\boldsymbol{j}}\) + 10\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = 14\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) – 6\(\hat{\boldsymbol{k}}\)
மற்றும் \(\vec{c}\) = 2\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\)
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) என்ற வெக்டர்கள் ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளை கொண்ட இணைகரத் திண்மத்தின் கன அளவு \(\vec{a}\).(\(\vec{b}\) × \(\vec{c}\))

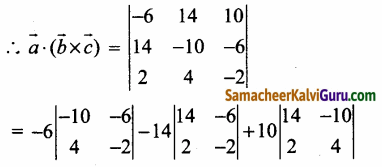
= -6(20 + 24) – 14(-28 + 12) + 10(56 + 20)
= -6(44) – 14(-16) + 10(76)
= -264 + 224 + 760 = 720.
∴ தேவையான இணைகரத்திண்மத்தின் கன அளவு = 720 கன அலகுகள்.

கேள்வி 3.
7\(\hat{\boldsymbol{i}}\) + λ\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\), \(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – \(\hat{\boldsymbol{k}}\) 3\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\) என்ற வெக்டர்களை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவு 90 கன அலகுகள்
எனில், -ன் மதிப்பைக் காண்க.
தீர்வு:
\(\vec{a}\) = 7\(\hat{\boldsymbol{i}}\) + λ\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = \(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – \(\hat{\boldsymbol{k}}\) மற்றும்
\(\vec{c}\) = 3\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\)
∴ இணைகரத்தின்மத்தின் கன அளவு = \(\vec{a}\) . (\(\vec{b}\) × \(\vec{c}\)) கொடுக்கப்பட்ட \(\vec{a}\) . (\(\vec{b}\) × \(\vec{c}\)) = 90
⇒ 7(10 + 7) – λ(5 – 3) – 3(7 + 6) = 90
⇒ 7(17) – λ(2) – 3(13) = 90
⇒ 119 – 2λ – 39 = 90
⇒ 119 – 39 – 90 = 2λ
⇒ -10 = 2λ
⇒ λ = -5

கேள்வி 4.
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) என்ற ஒரு தளம் அமையா மூன்று வெக்டர்களை ளை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவு 4 கன அலகுகள் எனில் (\(\vec{a}\) + \(\vec{b}\)) . (\(\vec{b}\) × \(\vec{c}\))+(\(\vec{b}\) + \(\vec{c}\)) . (\(\vec{c}\) × \(\vec{a}\)) + (\(\vec{c}\) + \(\vec{a}\)) . (\(\vec{a}\) × \(\vec{b}\)) – ன் மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட இணைகரத்தின் ஒரு புள்ளியில் சந்திக்கும் வெக்டர்கள் \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) மற்றும் அதனுடைய கொள்ளளவு 4 கன அலகுகள்
∴ \(\vec{a}\)(\(\vec{b}\) × \(\vec{c}\)) = ± 4 கன அலகுகள் …. (1)
கருதுக

கேள்வி 5.
\(\vec{b}\), \(\vec{c}\) என்ற வெக்டர்களால் உருவாக்கப்படும் இணைகரத்தை அடிப்பக்கமாக எடுத்துக் கொண்டு \(\vec{a}\) = -2\(\hat{\boldsymbol{i}}\) + 5\(\hat{\boldsymbol{j}}\) + 3\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = \(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) மற்றும் \(\vec{c}\) = -3\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + 4\(\hat{\boldsymbol{k}}\) என்ற வெக்டர்களால் உருவாக்கப்படும் இணைகரத் திண்மத்தின் உயரத்தைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட \(\vec{a}\) = -2\(\hat{\boldsymbol{i}}\) + 5\(\hat{\boldsymbol{j}}\) + 3\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = \(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) மற்றும் \(\vec{c}\) = -3\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + 4\(\hat{\boldsymbol{k}}\)
திண்ம இணைகரத்தின் கன அளவு = \(\vec{a}\) . (\(\vec{b}\) × \(\vec{c}\))

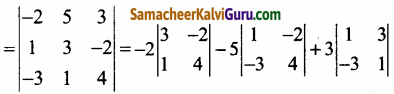
= -2(12 + 2) -5(4 – 6) + 3(1 + 9)
= -2(14) – 5(-2) + 3(10) = -28 + 10 + 30
= 12 ….. (1)
அடிப்பக்க இணைகரத்தின் வெக்டர் பரப்பு = \(\vec{b}\) × \(\vec{c}\)

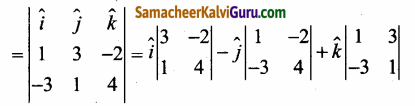
= \(\hat{\boldsymbol{i}}\)(12 + 2) – \(\hat{\boldsymbol{j}}\)(4 – 6) + \(\hat{\boldsymbol{k}}\)(1 + 9)
= \(\hat{\boldsymbol{i}}\)(14) – \(\hat{\boldsymbol{j}}\)(-2) + \(\hat{\boldsymbol{k}}\)(10) = 14\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) + 10\(\hat{\boldsymbol{k}}\)
இணைகரத்தின் பரப்பு = \(\sqrt{14^{2}+2^{2}+10^{2}}\)
= \(\sqrt{196+4+100}\) = \(\sqrt{300}\) = 10\(\sqrt{3}\) … (2)
திண்ம இணைகரத்தின் கன அளவு = அடிப்பரப்பு × உயரம்

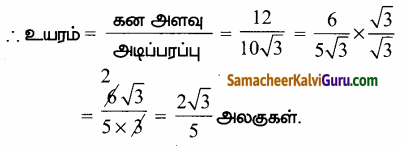
கேள்வி 6.
2\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) +\(\hat{\boldsymbol{k}}\), \(\hat{\boldsymbol{i}}\) – 2\(\hat{\boldsymbol{j}}\) + 2\(\hat{\boldsymbol{k}}\) மற்றும் 3\(\hat{\boldsymbol{i}}\)+ \(\hat{\boldsymbol{j}}\) + 3\(\hat{\boldsymbol{k}}\)
என்ற மூன்று வெக்டர்கள் ஒரு தள வெக்டர்களாகுமா எனக் காண்க.
தீர்வு:

= 2 (-6 – 2) – 3(3 – 6) + 1 (1 + 6)
= 2(-8) – 3(-3) + 1(7) = -16 + 9 + 7 = -16 + 16
= 0.
ஆகையால் கொடுக்கப்பட்ட வெக்டர்கள் ஒரு தள வெக்டர்களாகும்.

கேள்வி 7.
\(\overrightarrow{\boldsymbol{a}}\) = \(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + \(\hat{\boldsymbol{k}}\), \(\overrightarrow{\boldsymbol{b}}\) = \(\hat{\boldsymbol{i}}\) மற்றும் \(\overrightarrow{\boldsymbol{c}}\) = c₁\(\hat{\boldsymbol{i}}\) + c₂\(\hat{\boldsymbol{j}}\) + c₃\(\hat{\boldsymbol{k}}\) என்க. c₁ = 1 மற்றும் c₂ = 2 எனில் \(\overrightarrow{\boldsymbol{a}}\), \(\overrightarrow{\boldsymbol{b}}\), \(\overrightarrow{\boldsymbol{c}}\) என்ற வெக்டர்கள் ஒரு தள வெக்டர்களாக இருக்குமாறு c₃ -ன் மதிப்பினைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட

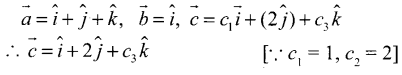
மேலும், கொடுக்கப்பட்ட \(\overrightarrow{\boldsymbol{a}}\), \(\overrightarrow{\boldsymbol{b}}\) மற்றும் \(\overrightarrow{\boldsymbol{c}}\) ஒரு தள வெக்டர்களாகும்.

கேள்வி 8.
\(\overrightarrow{\boldsymbol{a}}\) = \(\hat{\boldsymbol{i}}\) – \(\hat{\boldsymbol{k}}\), \(\overrightarrow{\boldsymbol{b}}\) = x\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + (1 – x)\(\hat{\boldsymbol{k}}\), \(\overrightarrow{\boldsymbol{c}}\) = y\(\hat{\boldsymbol{i}}\) + x\(\hat{\boldsymbol{j}}\) + (1 + x – y)\(\hat{\boldsymbol{k}}\), எனில் [\(\overrightarrow{\boldsymbol{a}}\), \(\overrightarrow{\boldsymbol{b}}\), \(\overrightarrow{\boldsymbol{c}}\)] என்பது x – யையும் y-யையும் பொறுத்து அமையாது என நிரூபிக்க.
தீர்வு:
கொடுக்கப்பட்ட \(\overrightarrow{\boldsymbol{a}}\) = \(\hat{\boldsymbol{i}}\) – \(\hat{\boldsymbol{k}}\), \(\overrightarrow{\boldsymbol{b}}\) = x\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) + (1 – x)\(\hat{\boldsymbol{k}}\), \(\overrightarrow{\boldsymbol{c}}\) = y\(\hat{\boldsymbol{i}}\) + x\(\overrightarrow{\boldsymbol{j}}\) + (1 – x – y)\(\hat{\boldsymbol{k}}\)

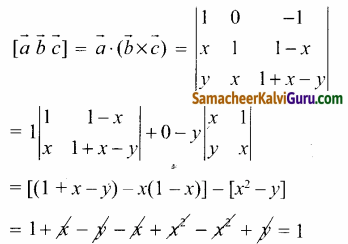
∴ [\(\overrightarrow{\boldsymbol{a}}\) \(\overrightarrow{\boldsymbol{b}}\) \(\overrightarrow{\boldsymbol{c}}\)] = 1 x- மற்றும் yஎன் எல்லா மதிப்புகளுக்கும்
∴ [\(\overrightarrow{\boldsymbol{a}}\) \(\overrightarrow{\boldsymbol{b}}\) \(\overrightarrow{\boldsymbol{c}}\)] x -யையும் y-யையும் பொறுத்து அமையாது.

கேள்வி 9.
a\(\hat{\boldsymbol{i}}\) + a\(\hat{\boldsymbol{j}}\) + c\(\hat{\boldsymbol{k}}\), \(\hat{\boldsymbol{i}}\)+\(\hat{\boldsymbol{k}}\) மற்றும் c\(\hat{\boldsymbol{i}}\) + c\(\hat{\boldsymbol{j}}\) + b\(\hat{\boldsymbol{k}}\) என்ற வெக்டர்கள் ஒரு தள வெக்டர்கள் எனில், a மற்றும் ம் ஆகியவற்றின் பெருக்குச் சராசரி c ஆகும் என நிரூபிக்க.
தீர்வு:
\(\vec{a}\) = a\(\hat{\boldsymbol{i}}\) + a\(\hat{\boldsymbol{j}}\) + c\(\hat{\boldsymbol{k}}\), \(\vec{b}\) = \(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{k}}\), \(\vec{c}\) = c\(\hat{\boldsymbol{i}}\) + c\(\hat{\boldsymbol{j}}\) + b\(\hat{\boldsymbol{k}}\) கொடுக்கப்பட்ட \(\vec{a}\), \(\vec{b}\) மற்றும் \(\vec{c}\) ஒரு தள வெக்டர்கள்

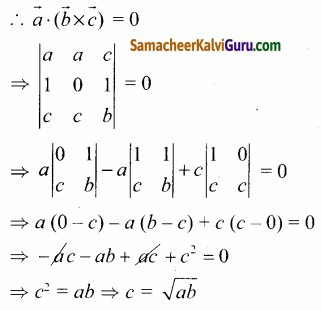
எனவே a மற்றும் b யின் பெருக்குச் சராசரி c ஆகும்.

கேள்வி 10.
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) என்ற பூச்சியமற்ற மூன்று வெக்டர்களில்
\(\vec{a}\), \(\vec{b}\) என்ற வெக்டர்களுக்கு செங்குத்தான அலகு வெக்டர் \(\vec{c}\) என்க. \(\vec{a}\), \(\vec{b}\) என்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் \(\frac{\pi}{6}\) எனில், [\(\vec{a}\), \(\vec{b}\), \(\vec{c}\)]² = \(\frac{1}{4}|\vec{a}|^{2}|\vec{b}|^{2}\) என நிறுவுக.
தீர்வு:
|\(\vec{c}\)| = 1 மற்றும் \(\vec{c}\) ⊥ \(\vec{a}\) மற்றும் \(\vec{b}\)
மேலும், \(\vec{a}\) மற்றும் \(\vec{b}\) க்கு இடையேயான கோணம் \(\frac{\pi}{6}\)