Samacheer Kalvi 12th Maths Guide Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.4

கேள்வி 1.
(5,2) என்ற புள்ளியிலிருந்து 2x² + 7y² = 14 என்ற நீள்வட்டத்திற்கு வரையப்படும் தொடு
கோடுகளின் சமன்பாடுகளைக் காண்க.
தீர்வு:
நீள் வட்டத்தின் சமன்பாடு 2x² + 7y² = 14
÷ 14 நமக்கு கிடைப்பது \(\frac{x^{2}}{7}\) + \(\frac{y^{2}}{2}\) = 1
∴ a²= 7, b² = 2
y = mx + c என்ற நேர்க்கோடு நீள்வட்டத்தின் தொடுகோடாக இருக்க கட்டுப்பாடு
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) …. (1)
(5, 2), (1) ன் மீதுள்ள து மற்றும் a² = 7, b² = 2
∴ 2 = m(5) ± \(\sqrt{7 m^{2}+2}\) + 2
2 – 5m = ± \(\sqrt{7 m^{2}+2}\)
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது
(2 – 5m)² = 7m² + 2
4 + 25m² – 20m = 7m² + 2
18m² – 2m + 2 = 0
9m² – 10m + 1 = 0 (÷2)

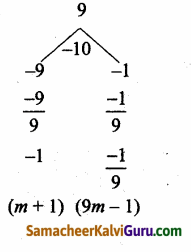
காரணிபடுத்த கிடைப்பது
(m – 1)(9m – 1) = 0
∴ m – 1 = 0 (அ)
9m – 1 = 0
⇒ m = 1 (அ)\(\frac{1}{9}\)
m = 1 எனில், (1) லிருந்து
y = 1(x) ± \(\sqrt{7 m^{2}+2}\)
⇒ y = x ± \(\sqrt{7+2}\) ⇒ y = x ± 3
y = x + 3 ⇒ x – y + 3 = 0
m = \(\frac{1}{9}\) எனில் (1)லிருந்து

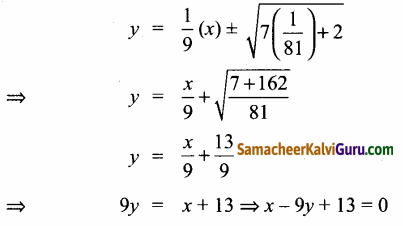
ஆகையால் தொடுகோட்டின் சமன்பாடுகள் x – y + 3 = 0 மற்றும் x – 9y + 13 = 0.

கேள்வி 2.
\(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{64}\) = 1 என்ற அதிபரவளையத்திற்கு, 10x – 3y + 9 = 0 என்ற நேர்க்கோட்டிற்கு இணையான தொடுகோட்டுச் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட அதிபரவளையத்தின் சமன்பாடு
\(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{64}\) = 1
y = mx + c என்பது தேவையான தொடுகோடு என்க.
⇒ a² = 16 மற்றும் b² = 64
தொடுகோடுகள் 10x – 3y + 9 = 0 க்கு இணையானது.
∴ தொடுகோட்டின் சாய்வு (m)
= 10x – 3y + 9 = 0 கோட்டின் சாய்வு.

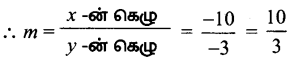
y = mx + c என்பது தேவையான தொடுகோடு என்க c² = a²m² – b²


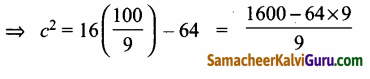
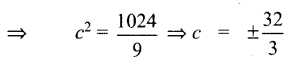
∴ தேவையான தொடுகோடுகள்
y = \(\frac{10}{3}\)x + \(\frac{32}{3}\), அல்லது y = \(\frac{10 x}{3}\) + \(\frac{32}{3}\)
⇒ 3y = 10x + 32 அல்ல து 3y = 10x – 32
⇒ 10x – 3y + 32 = 0 அல்ல து
10x – 3y – 32 = 0

கேள்வி 3.
x – y + 4 = 0 என்ற நேர்க்கோடு x² + 3y² = 12 என்ற நீள்வட்டத்தின் தொடுகோடு என நிறுவுக.
மேலும் தொடும் புள்ளியைக் காண்க.
தீர்வு:
நீள் வட்டத்தின் சமன்பாடு x² + 3y² = 12
÷ 12 கிடைப்பது \(\frac{x^{2}}{12}\) + \(\frac{y^{2}}{4}\) = 1
கோடு x – y + 4 = 0 ஐ y = x + 4 என திருத்தி எழுதலாம்.
∴ m = 1, c = 4
y = mx + 4 நீள் வட்டத்தின் தொடுகோடாக இருக்க கட்டுப்பாடு c² = a²m² + b²
∴ (4)² = 12(1)² + 4
⇒ 16 = 12 + 4
நிபந்தனை நிறைவு செய்யப்படுவதால், கோடு x – y + 4 = 0 நீள் வட்டம் x² + 3y² = 12 க்கு தொடுகோடாகும்.
மேலும் தொடுபுள்ளி \(\left(-\frac{a^{2} m}{c}, \frac{b^{2}}{c}\right)\)
\(\left(-\frac{12(1)}{4}, \frac{4}{4}\right)\) ⇒ (-3, 1)
∴ தொடுபுள்ளி (-3, 1).

கேள்வி 4.
y² = 16x என்ற பரவளையத்திற்கு, 2x + 2y + 3 = 0 என்ற கோட்டிற்குச் செங்குத்தான தொடு கோட்டுச் சமன்பாடு காண்க.
தீர்வு:
பரவளையத்தின் சமன்பாடு y² = 16x
∴ 4a = 16 ⇒ a = 4
y = mx + c என்க. …. (1)
என்பது பரவளையத்தின் தொடுகோடு என்க. 2x + 2y + 3 = 0, தொடுகோடுக்கு செங்குத்து
ஆதலால்

y = mx + c பரவளையத்திற்கு தொடுகோடாக இருக்க நிபந்தனை c = \(\frac{a}{m}\)
∴ c = \(\frac{4}{1}\) = 4
(1)லிருந்து , y = 1(x) + 4 ⇒ x – y + 4 = 0
தேவையான தொடுகோடு.

கேள்வி 5.
y² = 8x என்ற பரவளையத்திற்கு t = 2 இல் தொடு கோட்டுச் சமன்பாடு காண்க. (குறிப்பு : துணையலகு வடிவத்தைப் பயன்படுத்துக)
தீர்வு:
பரவளையத்திற்கான சமன்பாடு y² = 8x
∴ 4a = 8 ⇒ a = 2
பரவளையத்திற்கான தொடுகோட்டின் துணையலகு வடிவம் yt = x + at²
t = 2 எனில், தொடுகோட்டின் சமன்பாடு
y(2) = x + 2(2)² ⇒ 2y = x +8
⇒ x – 2y + 8 = 0 தேவையான தொடுகோட்டின் சமன்பாடாகும்.

கேள்வி 6.
12x² – 9y² = 108 என்ற அதிபரவளையத்திற்கு θ = \(\frac{\pi}{3}\) இல் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க. (குறிப்பு: துணையலகு வடிவத்தைப் பயன்படுத்துக)
தீர்வு:
அதிபரவளையத்தின் சமன்பாடு 12x² – 9y² = 108
÷ 108 கிடைப்பது, \(\frac{12 x^{2}}{108}\) – \(\frac{9 y^{2}}{108}\) = 1
⇒ \(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{12}\) = 1
∴ a² = 9, b² = 12
அதிபரவளையத்திற்கான தொடுகோட்டின் துணையலகு சமன்பாடு \(\frac{x \sec \theta}{a}\) – \(\frac{y \tan \theta}{b}\) = 1
θ = \(\frac{\pi}{3}\) எனில், சமன்பாடு

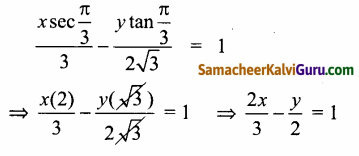
⇒ \(\frac{4 x-3 y}{6}\) = 1 ⇒ 4x – 3y – 6 = 0 தேவையான
தொடுகோட்டின் சமன்பாடு. பரவளையத்திற்கான செங்கோட்டின் துணையலகுச் சமன்பாடு

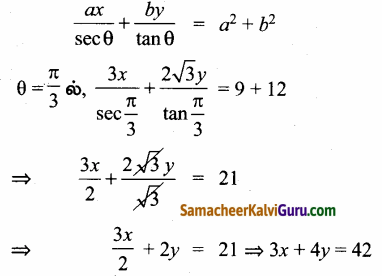
⇒ 3x + 4y – 42 = 0 தேவையான செங்கோட்டின் சமன்பாடாகும்.

கேள்வி 7.
y² = 4ax என்ற பரவளையத்திற்கு ‘t₁‘ மற்றும் ‘t₂‘ ஆகிய புள்ளிகளில் அமையும் தொடுகோடுகள் [at₁t₂a(t₁ + t₂)] என்ற புள்ளியில் சந்திக்கின்றன
என நிறுவுக.
தீர்வு:
y² = 4ax என்ற பரவளையத்திற்கு ‘t₁‘ -ல் தொடுகோட்டிற்கான துணையலகுச் சமன்பாடு yt₁ = x + \(a t_{1}^{2}\) …. (1)
மேலும், y² = 4ax என்ற பரவளையத்திற்கு ‘t₂‘ -ல் தொடுகோட்டிற்கான துணையலகுச் சமன்பாடு yt₂ = x + \(a t_{2}^{2}\) … (2)

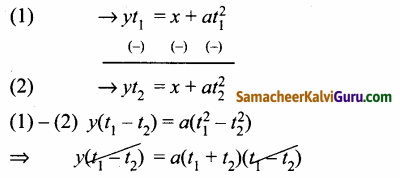
⇒ y = a(t₁ + t₂)
y = a(t₁ + t₂) என (1)-ல் பிரதியிட கிடைப்பது,
a(t₁ + t₂)t₁ = x + a\(t_{1}^{2}\)

இரண்டு நீளங்களின் வெட்டும் புள்ளி
[at₁t₂, a(t₁ + t₂)]

கேள்வி 8.
y² = 4ax என்ற பரவளையத்திற்கு ‘t₁‘ என்ற புள்ளியில் வரையப்படும் செங்கோடு, பரவளையத்தை மீண்டும் ‘t₂‘ என்ற புள்ளியில் சந்திக்குமெனில், t₂ = –\(\left(t_{1}+\frac{2}{t_{1}}\right)\) என நிறுவுக.
தீர்வு:
y² = 4ax என்ற பரவளையத்திற்கு ‘t₁‘ -ல் செங்கோட்டின் சமன்பாடு y + xt₁ = a\(t_{1}^{3}\) + 2at₁, …(1)
பரவளையம் y₂ = 4ax ஐ (1) ‘t₂ல் சந்திக்கிறது.
‘t₂‘-ல் பரவளையத்தின் மீதுள்ள புள்ளி, x = at², y = 2at₂, (2) ஆனது (1) ன் மீது அடைகிறது.
∴ (2) ஐ (1) -ல் பிரதியிட கிடைப்பது,

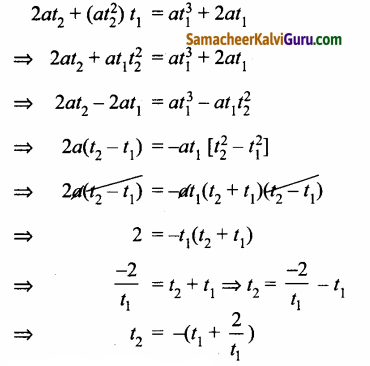
எனவே நிரூபிக்கப்பட்டது.