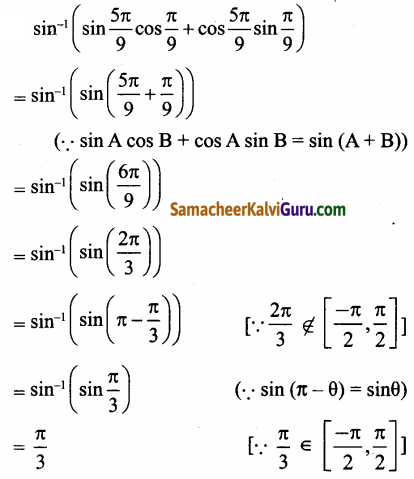Samacheer Kalvi 12th Maths Guide Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.1

Question 1.
x-ன் அனைத்து மதிப்புகளையும் காண்க.
(i) -10π ≤ x ≤ 10π மற்றும் sin x = 0
(ii) -8π ≤ x ≤ 8π and sin x = -1.
தீர்வு:
(i) கொடுக்கப்பட்ட sin x = 0
⇒ sin x = sin 0 ⇒ x = nπ, n ∈ Z.
-10π ≤ x ≤ 10π, n ஆனது-1 லிருந்து-10 லிருந்து +10 எடுத்துக் கொள்ளலாம்.
∴ x = nπ, இங்கு n = 0, ±1, ±2, ±3, ±4, ±5, ±6, ±7, ±8, ±9, ±10

(ii) sinx = -1
⇒ sin x = sin \(\left(\frac{-\pi}{2}\right)\) ⇒ x = \(\frac{-\pi}{2}\), \(\frac{3 \pi}{2}\), \(\frac{7 \pi}{2}\), ….
⇒ x = (4n – 1)\(\frac{\pi}{2}\) ; n ∈ z. ⇒ x= (4n – 1)\(\frac{\pi}{2}\); n எடுத்துக் கொள்ளும் மதிப்புகள் 0, ±1, ±2, ±3 மற்றும் ±4
ஆதலால் n = -4 எனில், x = \(\frac{-17 \pi}{2}\) < -8π.

Question 2.
பின்வருவனவற்றின் காலம் மற்றும் வீச்சு காண்க.
(i) y = sin 7x
(ii) y = – sin \(\left(\frac{1}{3} x\right)\)
(iii) y = 4sin(-2x).
தீர்வு:
(i) கொடுக்கப்பட்ட y = sin 7x
sinx- ன் வீச்சு 1 (சைன் வளைவரையின் மீப்பெரு மதிப்பு 1]
⇒ sin 7x -ன் வீச்சும் கூட 1.
சார்பின் காலம் p எனில் f(x + p) = f(x).
சைன் சார்பின் காலம் 2π. ஆதலால் sin 7x ன் காலம் \(\frac{2 \pi}{7}\) ஏனெனில் sin 7 \(\left(\frac{2 \pi}{7}\right)\) = sin 2π.

(ii) y = – sin\(\left(\frac{1}{3} x\right)\) sin x -ன் வீச்சு 1
⇒ – sin\(\left(\frac{1}{3} x\right)\)ன் வீச்சும் மேலும் 1.
– sin\(\left(\frac{1}{3} x\right)\) ன் காலம் \(\left(\frac{1}{3} x\right)\) = 2π ⇒ x = 6π.

(iii) y = 4 sin (-2x)
sin x -ன் வீச்சு1
⇒ sin (-2x) -ன் வீச்சு 1.
∴ 4 sin(-2x)-ன் வீச்சு 4 × 1 = 4.
sin(-2x) ன் காலம் 2x = 2π ⇒ x = \(\frac{2 \pi}{2}\) = π

Question 3.
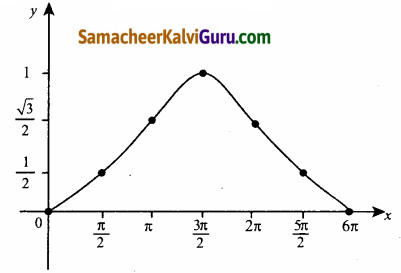
0 ≤ x ≤ 6π எனும் போது y = sin\(\left(\frac{1}{3} x\right)\) ன் வரைபடம் வரைக.
தீர்வு :

மற்றும் 6π, 0) என்ற புள்ளிகளை குறி

Question 4.
மதிப்பு காண்க
(i) \(\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)\)
(ii) \(\sin ^{-1}\left(\sin \left(\frac{5 \pi}{4}\right)\right)\)
தீர்வு:
(i)

(ii)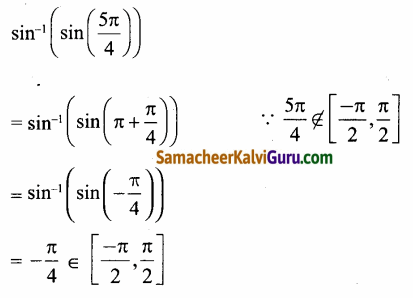

Question 5.
x-ன் எந்த மதிப்பிற்கு sin x = sin^-1x ஆகும்?
தீர்வு:
y = sin^-1x என்க.
y = 0, 0 = sin^-1x எனில்
⇒ sin(0) = sin(sin^-1(x))
⇒ sin 0 = x
⇒ x = 0
∴ x = 0 எனில் மட்டும் sin x = sin^-1x

Question 6.
பின்வருவனவற்றிற்கு சார்பகம் காண்க.
(i) f(x) = sin^-1\(\left(\frac{x^{2}+1}{2 x}\right)\)
(ii) g(x) = 2 sin^-1(2x – 1) – \(\frac{\pi}{4}\)
தீர்வு:
(i) கொடுக்கப்பட்ட f(x) = sin^-1\(\left(\frac{x^{2}+1}{2 x}\right)\)
நமக்கு தெரியும் sin(x) -ன் சார்பகம் [-1, 1]

(1) மற்றும் (2) லிருந்து சார்பகம் = {-1, 1}

(ii) g(x) = 2 sin^-1(2x – 1)-\(\frac{\pi}{4}\)
sin^-1x ன் வரையறையிலிருந்து
-1 ≤ 2x – 1 ≤ 1
⇒ -1+1 ≤ 2x ≤ 1 + 1 ⇒ 0 ≤ 2x ≤ 2
⇒ 0 ≤ x ≤ 1
∴ சார்பகம் = [0, 1]

Question 7.
மதிப்பு காண்க sin^-1 (sin \(\frac{5 \pi}{9}\) cos\(\frac{\pi}{9}\) + cos \(\frac{5 \pi}{9}\) sin\(\frac{\pi}{9}\))
தீர்வு: