Samacheer Kalvi 12th Maths Guide Chapter 3 சமன்பாட்டியல் Ex 3.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 சமன்பாட்டியல் Ex 3.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 3 சமன்பாட்டியல் Ex 3.5

கேள்வி 1.
பின்வரும் சமன்பாடுகளைத் தீர்க்க :
(i) sin² x – 5 sin x + 4 = 0
(ii) 12x³ + 8x = 29x² – 4
தீர்வு:
(i) sin² x – 5 sin x + 4 = 0
பிரதியிடு y = sinx
⇒ y – 5y + 4 = 0
⇒ (y – 4)(y – 1) = 0
⇒ y = 4, 1
நிலை (i)
y = 4 எனில், sin x = 4
மற்றும் sin x = 4-க்கு தீர்வு இல்லை அதனுடைய | வீச்சகம் [-1, 1] ஆகும்.
நிலை (ii)
sin x = 1
⇒ sin x = sin \(\frac{\pi}{2}\) [∵ sin \(\frac{\pi}{2}\) = 1]
x = 2nπ + \(\frac{\pi}{2}\), n ∈ ℤ
[∵ sin x = sin α ⇒ x = 2nπ + α n ∈ ℤ]

(ii) 12x³ + 8x = 29x² – 4
இந்த சமன்பாட்டை பின்வருமாறு திருத்தி எழுதலாம்.
12x³ – 29x² + 8x + 4 = 0

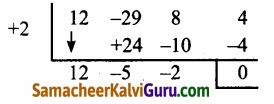
∴ x = 2 ஒரு மூலம் மற்றும் மீதியிருக்கும் காரணி 12x² – 5x – 2
⇒ (3x – 2)(4x + 1) = 0
3x – 2 = 0 (அ) 4x + 1 = 0

⇒ x = \(\frac{2}{3}\),
x = \(\frac{-1}{4}\)
∴ மூலங்கள் 2, \(\frac{2}{3}\) மற்றும் –\(\frac{1}{4}\).

கேள்வி 2.
விகிதமுறு மூலங்கள் உள்ளதா என ஆராய்க.
(i) 2x³ – x² – 1 = 0
(ii) x⁸ – 3x + 1 = 0
தீர்வு:
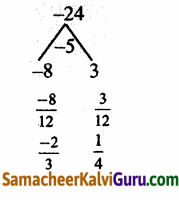
(i) 2x³ – x² – 1 = 0
கெழுக்களின் கூடுதல் = 2 – 1 – 1 = 0
x = 1 என்பது ஒரு மூலம்

∴ x = 1 ஒரு மூலம் மற்றும் மீதியிருக்கும் காரணி
2x² + x + 1

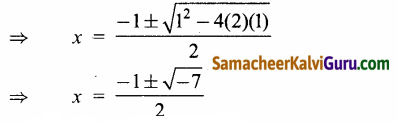
மூலம் என்பது ஒரு கலப்பெண்
⇒ x = \(\frac{-1 \pm i \sqrt{7}}{2}\)
∴x = 1 என்பது ஒரு விகிதமுறு மூலம்

(ii) x⁸ – 3x + 1 = 0
இங்கு a_n = 1, a₀ = 1
\(\frac{p}{q}\) பல்லுறுப்பு கோவையின் ஒரு மூலம்
இங்கு (p, q) = 1, a₀ = 1-ன் காரணி p மற்றும் a_n = 1-ன் காரணி q
1 க்கு காரணி இல்லை ஆதலால் கொடுக்கப்பட்ட சமன்பாட்டுக்கு விகிதமுறு மூலங்கள் இல்லை.

கேள்வி 3.
தீர்க்க : 8\(x^{\frac{3}{2 n}}\) – 8\(x^{\frac{-3}{2 n}}\) = 63
தீர்வு:

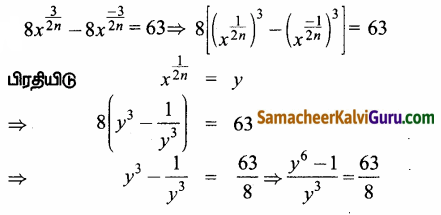
⇒ 8y⁶ – 8 = 63y³
⇒ 8y⁶ – 63y³ – 8 = 0
⇒ 8t² – 63t – 8 = 0 [இங்கு t = y³]
⇒ (8t – 1)(t – 8) = 0
⇒ t = \(\frac{1}{8}\), 8
நிலை (i) t = 8 எனில், ⇒ y³ = 8 ⇒ y³ = 2³
⇒ y = 2
நிலை (ii) t = \(\frac{1}{8}\) எனில், y³ = \(\frac{1}{8}\) = y ⇒ y = \(\frac{1}{2}\)
y = 2 எனில் \(x^{\frac{1}{2 n}}\) = 2
⇒ x = (2)²ⁿ ⇒ x = (2²)ⁿ
⇒ x = 4ⁿ

எனவே மூலங்கள் 4ⁿ.

கேள்வி 4.

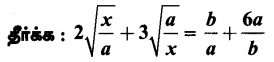
தீர்வு:

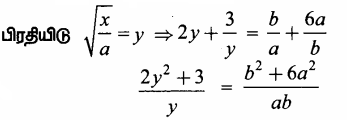
⇒ ab(2y² + 3) = (b² + 6a²)y
⇒ 2aby² + 3ab – y(b² + 6a²) = 0
⇒ 2aby² – y(b² + 6a²) + 3ab = 0
⇒ 2aby² – b²y – 6a²y + 3ab = 0
⇒ by(2ay – b) – 3a (2ay – b) = 0
⇒ (2ay – b) (by – 3a) = 0
⇒ 2ay = b, by = 3a
⇒ y = \(\frac{b}{2 a}\) y = \(\frac{3 a}{b}\)

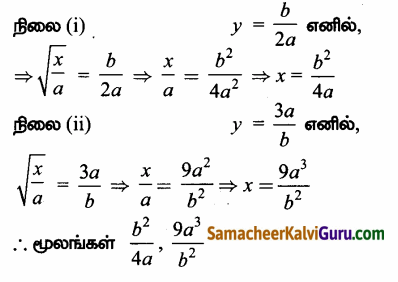
கேள்வி 5.
சமன்பாடுகளைத் தீர்க்க :
(i) 6x⁴ – 35x³ + 62x² – 35x + 6 = 0
(ii) x⁴ + 3x³ – 3x – 1 = 0
தீர்வு:
(i) 6x⁴ – 35x³ + 62x² – 35x + 6 = 0
இது இரட்டைப்படை முதல் வகை தலைகீழே சமன்பாடாகும்.
எனவே பின்வருமாறு எழுதலாம்.

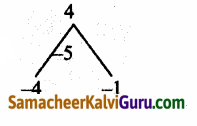
∴ (1) ஆனது,

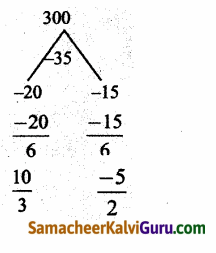
⇒ 6(y² – 2) – 35y + 62 = 0
⇒ 6y² – 12 – 35y + 62 = 0
⇒ 6y² – 35y + 50 = 0
⇒ (3y – 10) (2y – 5) = 0
⇒ y = \(\frac{10}{3}\), \(\frac{5}{2}\)
நிலை (i) y = \(\frac{10}{3}\)– எனில், x + \(\frac{1}{x}\) = \(\frac{10}{3}\)
⇒ \(\frac{x^{2}+1}{x}\) = \(\frac{10}{3}\)

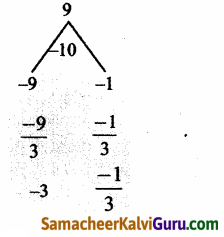
⇒ 3x² + 3 = 10x
⇒ 3x² – 10x + 3 = 0
⇒ (x – 3)(3x – 1) = 0
⇒ x = 3, \(\frac{1}{3}\)
நிலை (ii)
y = \(\frac{5}{2}\) எனில்,
x + \(\frac{1}{x}\) = \(\frac{5}{2}\) ⇒ \(\frac{x^{2}+1}{x}\) = \(\frac{5}{2}\)
⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0

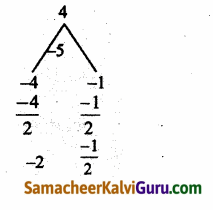
⇒ (x – 2) (2x – 1) = 0
⇒ x = 2, \(\frac{1}{2}\)
எனவே மூலங்கள் 2,\(\frac{1}{2}\), 3, \(\frac{1}{3}\)

(ii) x⁴ + 3x – 3x – 1=0
கெழுக்களின் கூடுதல் = 1 + 3 – 3 – 1 = 0
⇒ x = 1 என்பது ஒரு மூலம்
⇒ (x – 1) ஒரு காரணி

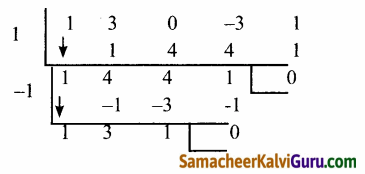
[தொகுமுறை வகுத்தலை பயன்படுத்தி]
x= 1,- 1 மூலங்கள் மற்றும் மீதியுள்ள காரணி x² + 3x + 1]

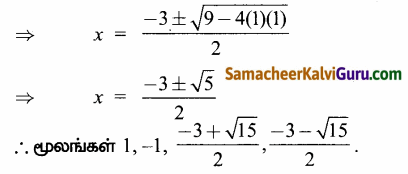
கேள்வி 6.
4^x – 3(2^x+2) + 2⁵ = 0 எனும் சமன்பாட்டை நிறைவு செய்யும் அனைத்து மெய்யெண்களையும் காண்க.
தீர்வு:
4^x – 3(2^x+2) + 25 = 0
⇒ (2²)^x – 3(2^x) + 2⁵ = 0
⇒ (2^x)² – 12(2^x) + 32 = 0

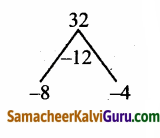
பிரதியிடு
2^x = y
y² – 12y + 32 = 0
(y – 8) (y – 4) = 0
y = 8, 4
நிலை (i)
y = 8 எனில், 2^x ⇒ 8 = 2^x = 2³ ⇒ x = 3 நிலை (ii)
y = 4 எனில், 2^x = 4 ⇒ 2^x = 2² ⇒ x = ± 2.
∴ மூலங்கள் 2, 3, -2.

கேள்வி 7.
6x⁴ – 5x³ – 38x² – 5x + 6 = 0 எனும் சமன்பாட்டின் ஒரு தீர்வு \(\frac{1}{3}\) எனில், சமன்பாட்டின் தீர்வு காண்க.
தீர்வு:
இது இரட்டைப்படை இரண்டாம் வகை தலைகீழ்
சமன்பாடாகும். எனவே இதனை பின்வருமாறு மாற்றி எழுதலாம்.
6(x² + \(\frac{1}{x^{2}}\)) – 5(x + \(\frac{1}{x}\)) – 38 = 0 … (1)
பிரதியிடு x + \(\frac{1}{x}\) ⇒ y = (x + \(\frac{1}{x}\))² = y²
⇒ x² + \(\frac{1}{x^{2}}\) + 2 = y² ⇒ x² + \(\frac{1}{x}\) = y² – 2
∴ (1) லிருந்து,
⇒ 6(y² – 2) – 5y – 38 = 0

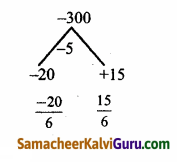
⇒ 6y² – 12 – 5y – 38 = 0
⇒ 6y² – 5y – 50 = 0
⇒ (3y – 10) (2y + 5) = 0
y = \(\frac{10}{3}\), \(\frac{-5}{2}\)
நிலை (i)
y = \(\frac{+10}{3}\)
x + \(\frac{1}{x}\) = \(\frac{+10}{3}\)
\(\frac{x^{2}+1}{x}\) = \(\frac{+10}{3}\)
⇒ 3x² + 3 = 10x
⇒ 3x² – 10x + 3 = 0
(x – 3)(x – \(\frac{1}{3}\)) = 0 ⇒ x = 3, \(\frac{1}{3}\)
நிலை (ii)
y = –\(\frac{5}{2}\) எனில்,
⇒ x + \(\frac{1}{x}\) = –\(\frac{5}{2}\) ⇒ \(\frac{x^{2}+1}{x}\) = \(\frac{-5}{2}\)
⇒ 2x² + 2 + 5x = 0 ⇒ 2x² + 5x + 2 = 0
⇒ (x + 2) (2x + 1) = 0 ⇒ x = -2, \(\frac{-1}{2}\)
∴ மூலங்கள் 3, \(\frac{1}{3}\), -2, \(\frac{-1}{2}\)