Samacheer Kalvi 12th Maths Guide Chapter 3 சமன்பாட்டியல் Ex 3.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 சமன்பாட்டியல் Ex 3.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 3 சமன்பாட்டியல் Ex 3.3

கேள்வி 1.
2x³ – x² – 18x + 9 = 0 எனும் முப்படி பல்லுறுப்புக்கோவைச் சமன்பாட்டின் மூலங்களில் இரண்டின் கூட்டுத்தொகை பூச்சியமெனில் சமன்பாட்டின் தீர்வு காண்க.
தீர்வு:
மூலங்களின் இரண்டின் கூட்டுத்தொகை பூச்சியம் ஆதலால் மூலங்கள் α, – α மற்றும் β என்க.
α – α + β = \(\frac{-b}{a}\) = \(\frac{1}{2}\)
β = \(\frac{1}{2}\)
மேலும், αβγ = \(\frac{-d}{a}\)
⇒ α(-α)(\(\frac{1}{2}\)) = \(\frac{-9}{2}\)
⇒ \(\frac{\alpha^{2}}{2}\) = \(\frac{9}{2}\) ⇒ α² = 9 ⇒ α = ±3
⇒ α = 3
∴ மூலங்கள் 3,-3 மற்றும் \(\frac{1}{2}\)

கேள்வி 2.
9x³ – 36x² + 44x – 16 = 0 -ன் மூலங்கள் கூட்டுத் தொடரில் அமைந்தவை எனில், சமன்பாட்டைத்
தீர்க்க.
தீர்வு:
இங்கு , a = 9, b = -36, c = 44, d = -16
மூலங்கள் கூட்டுத் தொடரில் அமைந்தவை ஆதலால், மூலங்கள் a – d, a மற்றும் a + d என்க.
மூலங்களின் கூடுதல் = \(\frac{-b}{a}\)
⇒ (a – d) + (a) + (a + d) = \(\frac{-(-36)}{9}\) = 4
⇒ 3a = 4 ⇒ a = \(\frac{4}{3}\) மற்றும்
மூலங்களின் பெருக்கல் பலன் = \(\frac{-d}{a}\)
\(\frac{-(-16)}{9}\) = \(\frac{(16)}{9}\)
⇒ (a – d) (a) (a + d) = \(\frac{(16)}{9}\)
(a² – d²) (a) = \(\frac{(16)}{9}\)

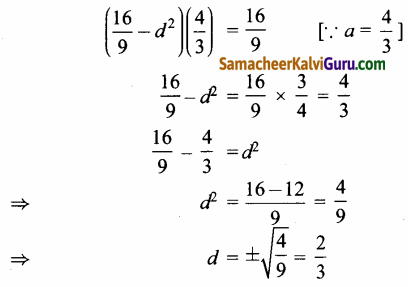
∴ மூலங்களாவன a – d, a, a + d
⇒ \(\frac{4}{2}\) – \(\frac{2}{3}\), \(\frac{4}{3}\), \(\frac{4}{3}\) + \(\frac{2}{3}\) ⇒ \(\frac{2}{3}\), \(\frac{4}{3}\), 2.

கேள்வி 3.
3x³ – 26x² + 52x – 24 = 0 – ன் மூலங்கள் பெருக்குத் தொடரில் அமைந்தவை எனில்,
சமன்பாட்டைத் தீர்க்க.
தீர்வு:
கொடுக்கப்பட்ட முப்படி சமன்பாடு
3x³ – 26x² + 52x – 24 = 0
இங்கு , a = 3, b = -2b, c = 52, d = -24.
மூலங்கள் பெருக்குத் தொடரில் அமைந்தவை ஆதலால்
மூலங்கள் \(\frac{a}{r}\) a, ar. மூலங்களின் கூடுதல் = –\(\frac{b}{a}\)
⇒ \(\frac{a}{r}\) + a + ar = \(\frac{26}{3}\) … (1)
மற்றும் மூலங்களின் பெருக்கல் பலன் = –\(\frac{d}{a}\)

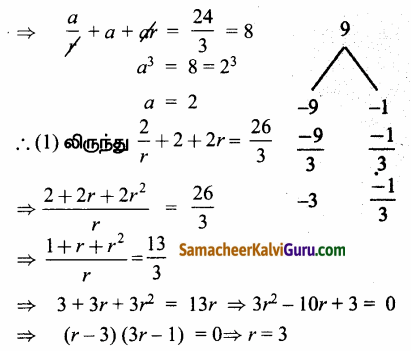
∴ மூலங்கள் \(\frac{a}{r}\), a, மற்றும் ar
⇒ \(\frac{2}{3}\) மற்றும் 2(3) ⇒ \(\frac{2}{3}\), 2 மற்றும் 6

கேள்வி 4.
2x³ – 6x² + 3x + k = 0 எனும் சமன்பாட்டின் ஒரு மூலம் மற்ற இரு மூலங்களின் கூடுதலின் இரு மடங்கு எனில், k – ன் மதிப்பைக் காண்க. மேலும் சமன்பாட்டைத் தீர்க்க.
தீர்வு:
கொடுக்கப்பட்ட முப்படி சமன்பாடு
2x³ – 6x² + 3x + k = 0
இங்கு , a = 2, b = -6, c = 3, d = k
α, β, γ என்பது மூலங்கள் என்க.
கொடுக்கப்பட்ட α = 2 (β + γ) ⇒ \(\frac{\alpha}{2}\) = β + γ …(1)


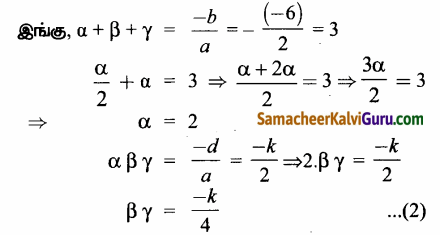
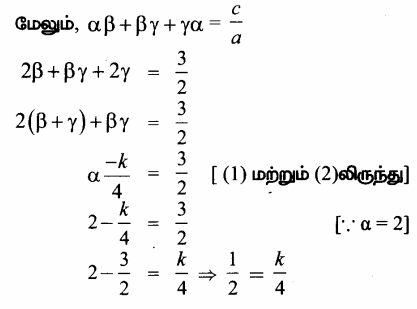
k = \(\frac{4}{2}\) ⇒ k = 2

கேள்வி 5.
1 + 2i மற்றும் \(\sqrt{3}\) ஆகியவைஸ்’ x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135, என்ற பல்லுறுப்புக் கோவையின் இரு பூச்சியமாக்கிகள் எனில்
அனைத்து பூச்சியமாக்கிகளையும் கண்டறிக.
தீர்வு:
f(x) = x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135 என்க.
கொடுக்கப்பட்ட (1 + 2i) ஒரு மூலம் ⇒ (1 – 2i) யும் ஒரு மூலம்
மேலும், \(\sqrt{3}\) ஒரு மூலம் –\(\sqrt{3}\) ஒரு மூலம்
எனவே f(x)-ன் காரணிகள் [x – (1 + 2i)]
[x – (1 – 2i)] [x – \(\sqrt{3}\)[x + \(\sqrt{3}\)]
[(x-1) – 2i] [(x – 1) + 2i][x – \(\sqrt{3}\)][x + \(\sqrt{3}\)] ((x – 1)² + 2²)(x² – 3)
= (x² – 2x + 1 + 4)(x² – 3)
⇒ f(x) ன் காரணிகள் (x² – 2x + 5)(x² – 3)
⇒ x⁴ – 3x² – 2x³ + 6x + 5x² – 15
⇒ (x⁴ – 2x³ + 2x² + 6x – 15), f(x)-ன் காரணி மற்ற காரணியை காண f(x) ஐ
x⁴ + 2x³ + 2x² + 6x – 15 ஆல் வகுக்க

மற்ற காரணியானது x² – x – 9

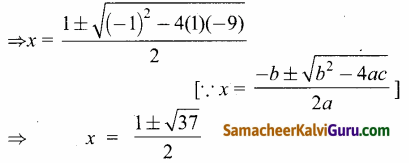
எனவே மற்ற மூலங்கள்
1 + 2i, 1 – 2i, \(\sqrt{3}\), –\(\sqrt{3}\), \(\frac{1+\sqrt{37}}{2}\), \(\frac{1-\sqrt{37}}{2}\)

கேள்வி 6.
பின்வரும் முப்படி சமன்பாடுகளைத் தீர்க்க :
(i) 2x³ – 9x² + 10x = 3,
(ii) 8x³ – 2x² – 7x + 3 = 0.
தீர்வு:
கெழுக்களின் கூடுதல்
2 – 9 + 10 – 3 = 12 – 12 = 0 ஆதலால்

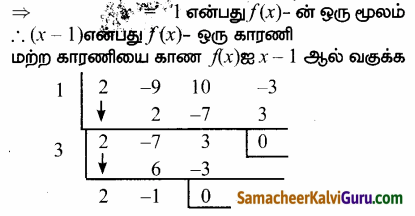
[தொகுமுறை வகுத்தலை பயன்படுத்தி)
f(x) = (x – 1) (x – 3) (2x – 1) = 0
⇒ x – 1 = 0, x – 3 = 0 or 2x – 1 = 0
⇒ x = 1, x = 3, x = \(\frac{1}{2}\)
எனவே மூலங்கள் 1, 3,\(\frac{1}{2}\)

(ii) f(x) = 8x³ – 2x² – 7x + 3 = 0 என்க இங்கு ஒற்றைப்படி உறுப்புகளின் கெழுக்களின் கூடுதல்
= 8 – 7 = 1
மற்றும் இரட்டைப்படி உறுப்புகளின் கெழுக்களின் கூடுதல்
= -2 + 3 = 1
எனவே, x = – 1 என்பது f(x) ன் ஒரு மூலமாகும் f(x) ஐ (x + 1) ஆல் வகுக்க

∴மற்ற காரணியானது 8x² – 10x + 3

கேள்வி 7.
x⁴ – 14x² + 45= 0 எனும் சமன்பாட்டைத் தீர்க்க.
தீர்வு:
x² = y என பிரதியிடு
⇒ y² – 14y+ 45 = 0

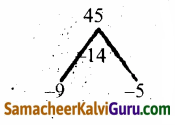
⇒ (y – 9) (y – 5) = 0
⇒ y = 9 (அ) y = 5
⇒ x² = 9 (அ) x² = 5
⇒ x = ±3 (அ) x = ±\(\sqrt{5}\)
எனவே, மூலங்கள் 3, -3, \(\sqrt{5}\) மற்றும் –\(\sqrt{5}\).