Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.4

கேள்வி 1.
கீழ்க்காணும் ஒரு சமவாய்ப்பு மாறி X-ன் நிகழ்தகவு நிறை சார்புகளுக்கு சராசரி மற்றும் பரவற்படி காண்க.
(i) f(x) = \(\left\{\begin{array}{ll}
\frac{1}{10} & x=2,5 \\
\frac{1}{5} & x=0,1,3,4
\end{array}\right.\)
(ii) f(x) = \(\left\{\frac{4-x}{6} x=1,2,3\right.\)

தீர்வு:
(i) கொடுக்கப்பட்ட f(x) = \(\left\{\begin{array}{ll}
\frac{1}{10} & x=2,5 \\
\frac{1}{5} & x=0,1,3,4
\end{array}\right.\)

f(x²) = Σx² f(x)

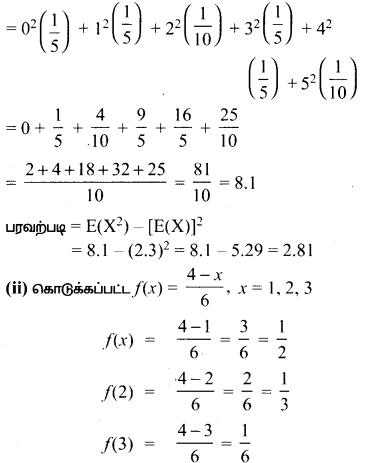
(ii) கொடுக்கப்பட்ட f(x) = \(\frac{4-x}{6}\), x = 1, 2, 3
f(x) = \(\frac{4-1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
f(2) = \(\frac{4-2}{6}\) \(\frac{2}{6}\) = \(\frac{1}{3}\)
f(3) = \(\frac{4-3}{6}\) = \(\frac{1}{6}\)
∴ நிகழ்தகவு நிறைச் சார்பு

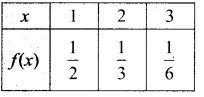
சராசரி = Σ(X) = Σxf(x)

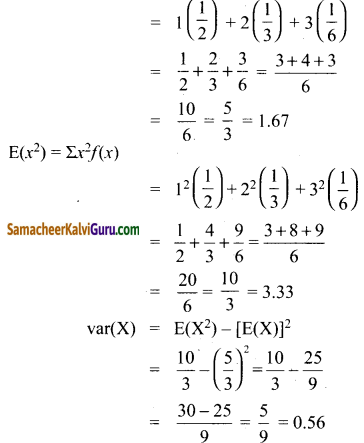
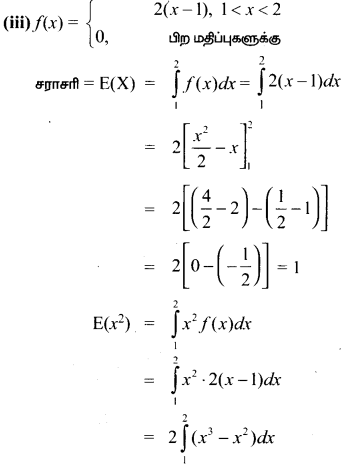
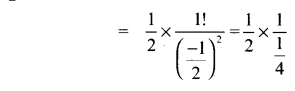
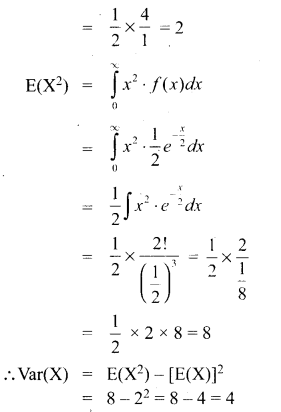
கேள்வி 2.
நான்கு சிவப்பு பந்துகள் மற்றும் மூன்று கருப்பு பந்துகள் கொண்ட ஒரு கூடையிலிருந்து பதிலீடாக இடாது அடுத்தடுத்து இரு பந்துகள் வெளியில் எடுக்கப்படுகின்றன. சிவப்பு பந்து வெளியில் எடுக்கும் சாத்திய கூறுகளை X என்க. X-ன் நிகழ்தகவு நிறை சார்பையும் சராசரியையும் காண்க.
தீர்வு:
கூறுவெளி = {4R, 3B}
X எடுக்கப்பட்ட சிவப்பு பந்துகளின் எண்ணிக்கை
X எடுத்துக் கொள்ளும் மதிப்புகள் 0, 1, 2
P(X = 0) = P(சிவப்பு பந்து இல்லை)

Σ(X) = Σx . f(x)
= 0(\(\frac{1}{7}\)) + 1(\(\frac{4}{7}\)) + 2(\(\frac{2}{7}\))
= \(\frac{4}{7}\) + \(\frac{4}{7}\) = 8

கேள்வி 3.
µ மற்றும் σ² ஆகியவை முறையே தனிநிலை சமவாய்ப்பு மாறி X-ன் சராசரி மற்றும் பரவற்படி மற்றும் E(X + 3) = 10 மற்றும் E(X + 3)² = 116 ,
எனில் 4 மற்றும் 5 காண்க.
தீர்வு:
கொடுக்கப்பட்ட E(X + 3) = 10
⇒ E(X) + 3 = 10
⇒ E(X) = 7
⇒ µ = 7 ……………….. (1)
E(X + 3)² = 116
E(X² + 6X + 9) = 116
E(X²) + 6E(X) + 9 = 116 [∵ E(9) = 9)
E(X²) + 6(7) + 9 = 116
E(X²) 116 – 42 – 9 = 116 – 51
E(X²) = 65 | ………..(2)
Var(X) = E(X²) – E(X)²
= 65 – 7² = 65 – 49 = 16
∴ u = 7 மற்றும் σ² = 16.

கேள்வி 4.
நான்கு சீரான நாணயங்கள் ஒரு முறை சுண்டப்படுகின்றன. தலைகளின் எண்ணிக்கை நிகழ்விற்கு நிகழ்தகவு நிறை சார்பு, சராசரி , மற்றும் பரவற்படி காண்க.
தீர்வு:
X என்பது தலைகளின் எண்ணிக்கையை குறிக்கிறது.
X எடுத்துக் கொள்ளும் மதிப்புகள் 0, 1, 2, 3, 4.
p(X = (0) = p(தலை இல்லை ) = p(TTT) = \(\frac{1}{16}\) } [∵ p(T) = \(\frac{1}{2}\), p(H) = \(\frac{1}{2}\)]

p(X = 1) = p(1 தலை) = 4C₁ × \(\frac{1}{16}\) = \(\frac{1}{4}\)

p(X = 2) = p(2 தலைகள்) = 4C₂ × \(\frac{1}{16}=\frac{4 \times 3}{\not 2 \times 1} \times \frac{1}{16}\)
= \(\frac{3}{8}\)

p(X = 3) = p(3 தலைகள்) = 4C₃ × \(\frac{1}{16}\) = 4 × \(\frac{1}{16}\)
= \(\frac{1}{4}\)

p(X = 4) = p(4 தலைகள்) = 4C₄ × \(\frac{1}{16}\) = \(\frac{1}{16}\)
∴ நிகழ்தகவு நிறைச் சார்பு

∴ Var(X) = E(X²) – [E(X)]²
= 5 – 2² = 5 – 4 = 1

கேள்வி 5.
ஒரு பயணிகள் இரயில் ஒவ்வொரு அரை மணி நேரத்திற்கும் ஒரு நிலையத்திற்கு சரியான நேரத்தில் வந்து சேரும். ஒவ்வொரு நாள் காலை யிலும், ஒரு மாணவர் தனது வீட்டிலிருந்து இரயில் நிலையத்திற்கு செல்கிறார். மாணவர் ரயில் நிலையத்தை அடையும் நேரத்திலிருந்து ரயிலுக்காக காத்திருக்கும் நேரத்தை X என நிமிடங்களில் குறிக்கலாம். X – ன் நிகழ்தகவு

எனில் சமவாய்ப்பு மாறி X-ன் நிகழ்தகவு அடர்த்தி சார்பு
தீர்வு:
கொடுக்கப்பட்ட f(x) =

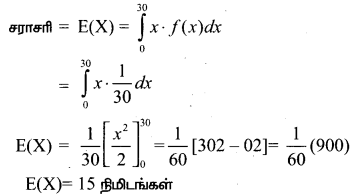
கேள்வி 6.
கணினி தயாரிக்கப்படும் போது ஆயிரக் கணக்கான மணிநேரம் பயன்படுத்தப்படும் ஒருமின்னணு சாதனமொன்றின் பழுதடையும் நேரத்தின் அடர்த்தி சார்பு

இம்மின்னனு சாதனத்தின் எதிர்பார்க்கப்படும் ஆயுட்காலத்தை காண்க.
தீர்வு:
கொடுக்கப்பட்ட f(x) =

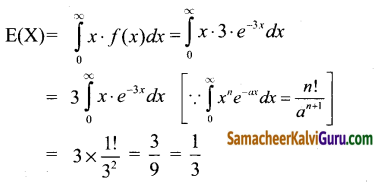
∴ மின்னனு சாதனத்தின் எதிர் பார்க்கப்படும் ஆயுட் காலம் \(\frac{1}{3}\) ஆகும்.

கேள்வி 7.
சமவாய்ப்பு மாறி X-ன்சராசரி நிகழ்தகவு அடர்த்தி சார்பு |
f (x) = \(\left\{\begin{aligned}
16 x e^{-4 x}, & x>0 \\
0, & x \leq 0
\end{aligned}\right.\) ஆகும் சமவாய்ப்பு மாறி X -ன் நிகழ்தகவு அடர்த்தி சார்பு.
தீர்வு:
கொடுக்கப்பட்ட f(x) =\(\left\{\begin{aligned}
16 x e^{-4 x}, & x>0 \\
0, & x \leq 0
\end{aligned}\right.\)

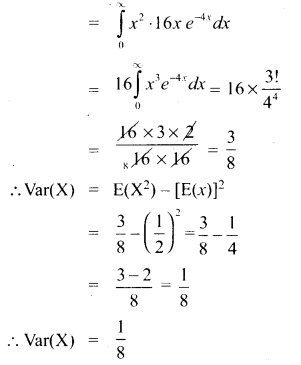
கேள்வி 8.
600 டிக்கெட்டுகள் கொண்ட ஒரு லாட்டரியில் ஒரு பரிசு 7.200 – க்கும் நான்கு பரிசுகள் ₹.100 – க்கும், ஆறு பரிசுகள் 1.50 – க்கும் எனக்கொடுக்கிறது. டிக்கெட் செலவு 7.2 என்றால், ஒரு டிக்கெட்டின் எதிர்பார்க்கப்படும் வெற்றி தொகையைக் கண்டறியவும்.
தீர்வு: