Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.1 Textbook Questions and Answers, Notes.
TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.1
கேள்வி 1.
பின்வரும் வகைக்கெழுச் சமன்பாடுகள் ஒவ்வொன்றின் வரிசை மற்றும் படி (இருக்குமானால்) ஆகியவற்றைத் தீர்மானிக்க.
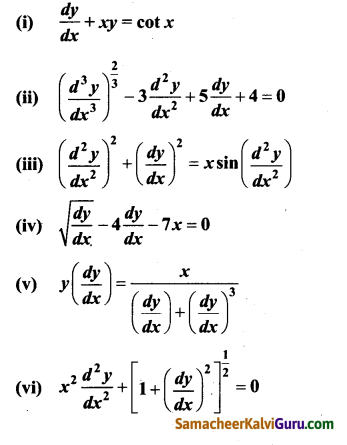
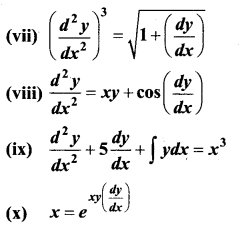
தீர்வு:
(i) \(\frac{d y}{d x}+x y=\cot x\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\frac{d y}{d x}\) + xy = cotx.
மிக உயர்ந்த வகைக்கெழு 1 மற்றும் அதனுடைய அடுக்கு 1
வரிசை 1, படி 1.
![]()
(ii) \(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{2}{3}}-3 \frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+4=0\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{2}{3}}-3 \frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+4=0\)
⇒ \(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{2}{3}}=3\left(\frac{d^{2} y}{d x^{2}}\right)-5\left(\frac{d y}{d x}\right)-4\)
மூன்றின் அடுக்கை இருபுறமும் எடுக்க கிடைப்பது,
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}=\left(3\left(\frac{d^{2} y}{d x^{2}}\right)-5\left(\frac{d y}{d x}\right)-4\right)^{3}\)
மிக உயர்ந்த வகைக்கெழு 3 மற்றும் அதனுடைய அடுக்கு 2
∴ வரிசை 3, படி 2.
(iii) \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\left(\frac{d y}{d x}\right)^{2}=x \sin \left(\frac{d^{2} y}{d x^{2}}\right)\)
மிக உயர்ந்த வகைக்கெழு 2
∴ வரிசை 2
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாட்டை வகைக்கெழுக்களால் ஆன பல்லுறுப்புக் கோவையாக எழுத இயலவில்லை. ஆதனால் அதனுடைய படி வரையறுக்கப்படவில்லை .
(iv) \(\sqrt{\frac{d y}{d x}}-4 \frac{d y}{d x}-7 x=0\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\sqrt{\frac{d y}{d x}}=4 \frac{d y}{d x}+7 x\)
இருபுறமும் வர்க்கப்படுத்த,

மிக உயர்ந்த வகைக்கெழு 1 மற்றும் அதனுடைய அதிகபட்ச அடுக்கு 2.
∴ வரிசை 1, படி 2.
(v) \(y\left(\frac{d y}{d x}\right)=\frac{x}{\left(\frac{d y}{d x}\right)+\left(\frac{d y}{d x}\right)^{3}}\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
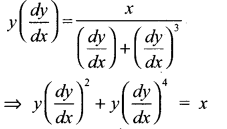
அதிகபட்ச வகைக்கெழு 1 மற்றும் அதனுடைய உயரிய அடுக்கு 4.
∴ வரிசை 4, படி 1
![]()
(vi) \(x^{2} \frac{d^{2} y}{d x^{2}}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{1}{2}}=0\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
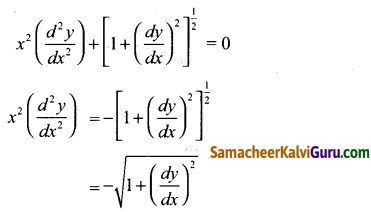
இருபுறமும் வகைப்படுத்த,
\(x^{4}\left(\frac{d^{2} y}{d x^{2}}\right)=1+\left(\frac{d y}{d x}\right)^{2}\)
உயரிய வகைக்கெழு 2 மற்றும் அதனுடைய அடுக்கு 2.
∴ வரிசை 2, படி 2.
(vii) \(\left(\frac{d^{2} y}{d x^{2}}\right)^{3}=\sqrt{1+\left(\frac{d y}{d x}\right)}\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{3}=\sqrt{1+\left(\frac{d y}{d x}\right)}\)
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது.
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{6}=1+\left(\frac{d y}{d x}\right)\)
உயரிய வகைக்கெழு 2 மற்றும் அதனுடைய அடுக்கு 6.
∴ வரிசை 2, படி 6.
![]()
(viii) \(\frac{d^{2} y}{d x^{2}}=x y+\cos \left(\frac{d y}{d x}\right)\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\frac{d^{2} y}{d x^{2}}=x y+\cos \left(\frac{d y}{d x}\right)\)
உயரிய வகைக்கெழு 2.
∴ வரிசை 2.
இச்சமன்பாடு வகைக்கெழுக்களை கொண்ட பல்லுறுப்புக் கோவைச் சமன்பாடல்ல. ஆகவே, இச்சமன்பாட்டின் படி வரையறுக்கப்படவில்லை.
(ix) \(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+\int y d x=x^{3}\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
\(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+\int y d x=x^{3}\)
‘x’ -ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(\frac{d^{3} y}{d x^{3}}+5 \frac{d^{2} y}{d x^{2}}+y=3 x^{2}\)
உயரிய வகைக்கெழு 3 மற்றும் அதனுடைய அடுக்கு 1.
∴ வரிசை 3 மற்றும் படி 1.
![]()
(x) x = \(e^{x y\left(\frac{d y}{d x}\right)}\)
கொடுக்கப்பட்ட வகைக்கெழு சமன்பாடு
x = \(e^{x y\left(\frac{d y}{d x}\right)}\)
⇒ log x = \(x y\left(\frac{d y}{d x}\right)\)
உயரிய வகைக்கெழு 1.
∴ படி 1.
இச்சமன்பாடு வகைக்கெழுக்களை கொண்ட பல்லுறுப்புக் கோவைச் சமன்பாடல்ல. ஆகவே, இச்சமன்பாட்டின் படி வரையறுக்கப்படவில்லை.