Samacheer Kalvi 12th Maths Guide Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.4

கேள்வி 1.
பின்வரும் நேரியச் சமன்பாடுகளின் தொகுப்பை கிராமரின் விதிப்படி தீர்க்க:
(i) 5x – 2y + 16 =0, x+3y-7 = 0
(ii) \(\frac{3}{x}\) + 2y = 12, \(\frac{2}{x}\) + 3y = 13
(iii) 3x+3y- = 11, 2x-y+27=9, 4x+3y+2z = 25
(iv) \(\frac{3}{x}\) – \(\frac{4}{y}\) – \(\frac{2}{z}\) – 1 = 0, \(\frac{1}{x}\) + \(\frac{2}{y}\) + \(\frac{1}{z}\) – 2 = 0, \(\frac{2}{x}\) – \(\frac{5}{y}\) – \(\frac{4}{z}\) + 1 = 0
தீர்வு:
(i) 5x – 2y =-16, x+3y = 7
கொடுக்கப்பட்ட △ = \(\left|\begin{array}{rr}
5 & -2 \\
1 & 3
\end{array}\right|\) = 15 + 2 = 17
△₁ = \(\left|\begin{array}{rr}
-16 & -2 \\
7 & 3
\end{array}\right|\) = -48 + 14 = -34
△₂ = \(\left|\begin{array}{rr}
5 & -16 \\
1 & 7
\end{array}\right|\) = 35 + 16 = 51

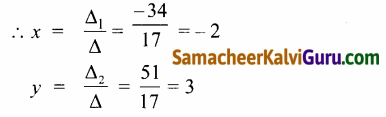
∴ தீர்வுக் கணம் {-2,3}

(ii) \(\frac{3}{x}\) + 2y=12, \(\frac{2}{x}\) + 3y = 13
\(\frac{1}{x}\) = z என்க
∴ 3z + 2y = 12, 2z + 3z = 13

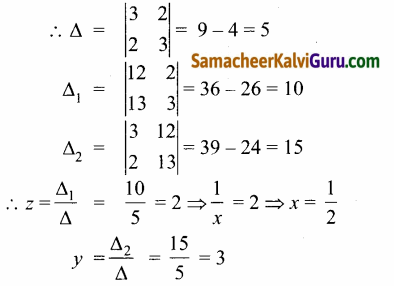
∴ தீர்வு கணம் {\(\frac{1}{2}\), 3}

(iii) 3x+3y-z = 11, 2x-y +2z = 9, 4x+ 3y +2z = 25
தீர்வு:
△ = \(\left|\begin{array}{ccc}
3 & 3 & -1 \\
2 & -1 & 2 \\
4 & 3 & 2
\end{array}\right|\)
= 3\(\left|\begin{array}{ll}
-1 & 2 \\
3 & 2
\end{array}\right|\) – 3\(\left|\begin{array}{ll}
2 & 2 \\
4 & 2
\end{array}\right|\) -1\(\left|\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right|\)
= 3(-2-6) – 3(4 – 8) – 1(6+ 4)
= 3(-8) – 3(- 4) – 1(10)
= – 24 + 12 – 10 =-22
△₁ = \(\left|\begin{array}{ccc}
11 & 3 & -1 \\
9 & -1 & 2 \\
25 & 3 & 2
\end{array}\right|\)
= 11\(\left|\begin{array}{ll}
-1 & 2 \\
3 & 2
\end{array}\right|\) -3\(\left|\begin{array}{ll}
9 & 2 \\
25 & 2
\end{array}\right|\) -1\(\left|\begin{array}{rr}
9 & -1 \\
25 & 3
\end{array}\right|\)
= 11(-2-6) -3(18-50) – 1(27 +25)
= 11(-8) -3(- 32) -1(52)
= – 88 + 96 – 52 = -44
△₂ = \(\left|\begin{array}{ccc}
3 & 11 & -1 \\
2 & 9 & 2 \\
4 & 25 & 2
\end{array}\right|\)
= 3\(\left|\begin{array}{cc}
9 & 2 \\
25 & 2
\end{array}\right|\) – 11\(\left|\begin{array}{ll}
2 & 2 \\
4 & 2
\end{array}\right|\) -1\(\left|\begin{array}{cc}
2 & 9 \\
4 & 25
\end{array}\right|\)
= 3(18-50) – 11(4-8) – 1(50-36)
= 3(- 32) – 11(- 4) – 1(14)
= – 96 + 44 – 14 = – 66
△₃ = \(\left|\begin{array}{ccc}
3 & 3 & 11 \\
2 & -1 & 9 \\
4 & 3 & 25
\end{array}\right|\)
= 3\(\left|\begin{array}{cc}
-1 & 9 \\
3 & 25
\end{array}\right|\) – 3\(\left|\begin{array}{rr}
2 & 9 \\
4 & 25
\end{array}\right|\) + 11\(\left|\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right|\)
= 3(-25-27)-3(50-36) + 11(6+4)
= 3(-52) – 3(14) + 11(10)
= -156 – 42 + 110 =-88

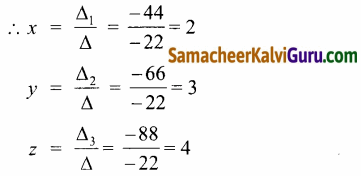
∴ தீர்வு கணம் {2, 3, 4}

(iv) \(\frac{3}{x}\) – \(\frac{4}{y}\) – \(\frac{2}{z}\) – 1 = 0, \(\frac{1}{x}\) + \(\frac{2}{y}\) + \(\frac{1}{z}\) – 2 = 0, \(\frac{2}{x}\) – \(\frac{5}{y}\) – \(\frac{4}{z}\) + 1 = 0
\(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v, \(\frac{1}{z}\)=w, என பிரதியிடு
நமக்கு கிடைப்பது 3u – 4v – 2w = 1, u + 2v + w = 2, 2u – 5v – 4v = -1
∴ △ = \(\left|\begin{array}{ccc}
3 & -4 & -2 \\
1 & 2 & 1 \\
2 & -5 & -4
\end{array}\right|\) = 3\(\left|\begin{array}{cc}
2 & 1 \\
-5 & -4
\end{array}\right|\) + 4\(\left|\begin{array}{cc}
1 & 1 \\
2 & -4
\end{array}\right|\) – 2\(\left|\begin{array}{cc}
1 & 2 \\
2 & -5
\end{array}\right|\)
= 3(- 8 + 5) + 4(- 4- 2) – 2(-5-4)
= 3(- 3) + 4(- 6) – 2(-9)
= -9 – 24 + 18 = – 15
△₁ = \(\left|\begin{array}{ccc}
1 & -4 & -2 \\
2 & 2 & 1 \\
-1 & -5 & -4
\end{array}\right|\)
= 1\(\left|\begin{array}{cc}
2 & 1 \\
-5 & -4
\end{array}\right|\) + 4\(\left|\begin{array}{cc}
2 & 1 \\
-1 & -4
\end{array}\right|\) -2\(\left|\begin{array}{cc}
2 & 2 \\
-1 & -5
\end{array}\right|\)
= 1(-8 +5) + 4(-8 + 1) – 2(- 10 + 2)
= 1(-3) + 4(-7) – 2(-8)
= -3 – 28 + 16 = -15
△₂ = \(\left|\begin{array}{ccc}
3 & 1 & -2 \\
1 & 2 & 1 \\
2 & -1 & -4
\end{array}\right|\)
= 3\(\left|\begin{array}{cc}
2 & 1 \\
-1 & -4
\end{array}\right|\) -1\(\left|\begin{array}{cc}
1 & 1 \\
2 & -4
\end{array}\right|\) -2\(\left|\begin{array}{rr}
1 & 2 \\
2 & -1
\end{array}\right|\)
= 3(-8+ 1) – 1(-4- 2)- 2(-1-4)
= 3(-7) – 1(-6) – 2(-5)
= -21 + 6 + 10 =-5
△₃ = \(\left|\begin{array}{ccc}
3 & -4 & 1 \\
1 & 2 & 2 \\
2 & -5 & -1
\end{array}\right|\)
= 3\(\left|\begin{array}{cc}
2 & 2 \\
-5 & -1
\end{array}\right|\) + 4\(\left|\begin{array}{rr}
1 & 2 \\
2 & -1
\end{array}\right|\) + 1\(\left|\begin{array}{cc}
1 & 2 \\
2 & -5
\end{array}\right|\)
= 3(- 2 + 10) + 4(- 1 – 4) + 1(- 5 – 4)
= 3(8) + 4(- 5) + 1(- 9)
= 24 – 20-9 =-5

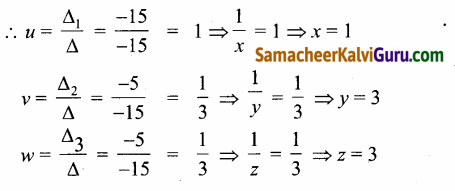
∴ தீர்வு கணம் {1, 3, 3}

கேள்வி 2.
ஒரு போட்டித் தேர்வில் ஒவ்வொரு சரியான விடைக்கும் ஒரு மதிப்பெண் வழங்கப்படுகிறது. ஒவ்வொரு தவறான விடைக்கும் \(\frac{1}{4}\) மதிப்பெண் குறைக்கப்படுகிறது. ஒரு மாணவர் 100 கேள்விகளுக்குப் பதிலளித்து 80 மதிப்பெண்கள் பெறுகிறார் எனில் அவர் எத்தனை கேள்விகளுக்குச் சரியாக பதில்! அளித்திருப்பார்? (கிராமரின் விதியைப் பயன்படுத்தி இக்கணக்கைத் தீர்க்கவும்).
தீர்வு:
x கேள்விகளுக்கு சரியாக பதில்
அளித்திருப்பார் மற்றும் ) கேள்விகளுக்கு தவறான பதில் அளித்திருப்பார் என்க. கொடுக்கப்பட்ட தரவின்படி, x+y=100 மற்றும்
1.x- \(\frac{1}{4}\)y = 80 …. (1)
4 ஆல் பெருக்க கிடைப்பது,
4x-y = 320 …. (2)
(1) மற்றும் (2) லிருந்து

∴84 கேள்விகளுக்குச் சரியான அளித்திருப்பார்.

கேள்வி 3.
வேதியாளர் ஒருவரிடம் 50% அமிலத்தன்மை கொண்ட ஒரு கரைசலும் மற்றும் 25% அமிலத்தன்மை கொண்ட மற்றொரு கரைசலும் உள்ளது. அவர் 10 லிட்டர் கரைசலில் 40% அமிலத்தன்மை உள்ளவாறு ஒரு கரைசலை உருவாக்க இருவகைக் கரைசல்கள் ஒவ்வொன்றிலிருந்தும் எத்தனை லிட்டர் சேர்க்க வேக வேண்டும்? (இக்கணக்கை
கிராமரின் விதியைப் பயன்படுத்தித் தீர்க்க).
தீர்வு:
50% அமிலத்தன்மை கரைசலிலிருந்து ர லிட்டர் மற்றும் 25% அமிலத்தன்மை கரைசலிலிருந்து y லிட்டர் சேர்க்க வேண்டும் என்க.
கொடுக்கப்பட்ட தரவின்படி, x+y= 10 …. (1)
மற்றும் x(\(\frac{50}{100}\)) + y(\(\frac{25}{100}\)) = 10(\(\frac{40}{100}\))
⇒ 50x + 25y = 400 ⇒ 2x+y= 16 … (2)
சமன்பாட்டுத் தொகுப்பின் அணி வடிவம்
⇒ AX = B இங்கு A = \(\left[\begin{array}{ll}
1 & 1 \\
2 & 1
\end{array}\right]\),
X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\), B = \(\left[\begin{array}{l}
10 \\
16
\end{array}\right]\)
⇒ X = A^-1B|A| = \(\left|\begin{array}{ll}
1 & 1 \\
2 & 1
\end{array}\right|\) = 1 – 2 = -1
⇒ X = \(\frac{1}{|\mathrm{~A}|}\)adj A.B
⇒ X = -1\(\left[\begin{array}{cc}
1 & -1 \\
-2 & 1
\end{array}\right]\)\(\left[\begin{array}{l}
10 \\
16
\end{array}\right]\)
= –\(\left[\begin{array}{c}
10-16 \\
-20+16
\end{array}\right]\)
⇒ X = –\(\left[\begin{array}{l}
-6 \\
-4
\end{array}\right]\) = \(\left[\begin{array}{l}
6 \\
4
\end{array}\right]\)
50% அமிலத்தன்மை கரைசலிலிருந்து 6 லிட்டர் மற்றும் 25% அமிலத்தன்மை கரைசலிலிருந்து 4 லிட்டர் சேர்க்க வேண்டும்.

கேள்வி 4.
ஒரு மீன் தொட்டியை பம்பு A மற்றும் பம்பு B என்பன ஒன்றாகச் சேர்ந்து 10 நிமிடங்களில் நீரை நிரப்பும். பம்பு B ஆனது நீரை உள்ளே அல்லது வெளியே ஒரே வேகத்தில் அனுப்ப இயலும். எதிர்பாராதவிதமாக பம்பு B ஆனது நீரை வெரை வெளியே அனுப்பினால் தொட்டி நிரம்ப 30 நிமிடங்கள் ஆகும் எனில் ஒவ்வொரு பம்பும் தொட்டியை தனித்தனியாக நிரப்ப எவ்வளவு காலம் எடுத்துக் கொள்ளும்? (கிராமரின் விதியைப் பயன்படுத்தி தீர்க்கவும்).
தீர்வு:
பம்பு A தொட்டியை நிரப்ப, நிமிடங்கள் எடுத்துக் கொள்ளும் மற்றும் பம்பு B தொட்டியை நிரப்பy நிமிடங்கள் எடுத்து கொள்ளும் என்க. 1 நிமிடத்தில் A ஆல் \(\frac{1}{x}\) அலகும் மற்றும் B ஆல் \(\frac{1}{y}\) அலகும் நிரப்ப முடியும்.

∴ \(\frac{1}{x}\) + \(\frac{1}{y}\) = 10
மற்றும் \(\frac{1}{x}\) – \(\frac{1}{y}\) = 30
\(\frac{1}{x}\) = aமற்றும் \(\frac{1}{y}\)=b என பிரதியிட
⇒ a + b = \(\frac{1}{10}\) …… (1)
மற்றும் a-b = \(\frac{1}{30}\) ….. (2)


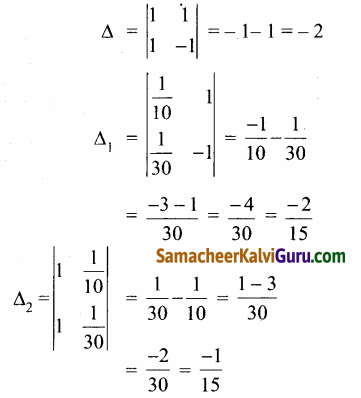
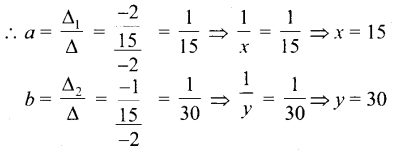
A 15 நிமிடங்களிலும், B 30 நிமிடங்களிலும் தொட்டியை நிரப்பும்.

கேள்வி 5.
ஒரு குடும்பத்திலுள்ள மூன்று நபர்கள் இரவு உணவு சாப்பிட ஓர் உணவகத்திற்குச் சென்றனர். இரு தோசைகள், மூன்று இட்லிகள் மற்றும் இரு வடைகளின் விலை ₹150. இரு தோசைகள், இரு இட்லிகள் மற்றும் நான்கு வடைகளின் விலை 1 200. ஐந்து தோசைகள், நான்கு இட்லிகள் மற்றும் இரண்டு வடைகளின் விலை ₹250. அக்குடும்பத்தினரிடம் ₹ 350 இருந்தது மற்றும் அவர்கள் மூன்று தோசைகள், ஆறு இட்லிகள் மற்றும் ஆறு வடைகள் சாப்பிட்டனர். அக்குடும்பத்தினர் சாப்பிட்ட செலவிற்கான தொகையை அவர்களிடமிருந்த பணத்தைக் கொண்டு செலுத்த முடியுமா?
(உமது விடையை கிராமரின் விதிக்கொண்டு நிரூபி)?
தீர்வு:
ஒரு தோசையின் விலை ₹x என்க.
ஒரு இட்லியின் விலை ₹y என்க.
ஒரு வடையின் விலை ₹z என்க.
கொடுக்கப்பட்ட தரவின்படி,
2x + 3y + 2z = 150
2x + 2y + 4z = 200
5x + 4y +2z = 250

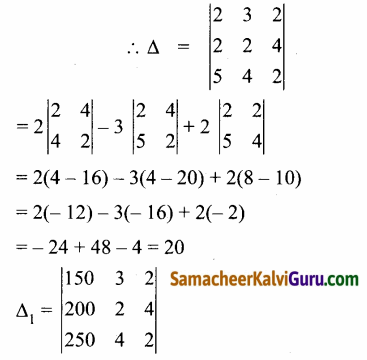
C₃, லிருந்து 50ஐ பொதுவில் எடுக்க கிடைப்பது,

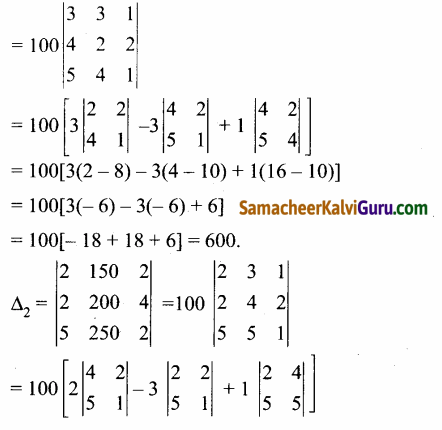
= 100[2(4 – 10) – 3(2 – 10) + 1(10 – 20)]
= 100[2(- 6) – 3(-8) + 1(- 10)]
= 100[- 12 + 24 – 10] = 100 [2] = 200.

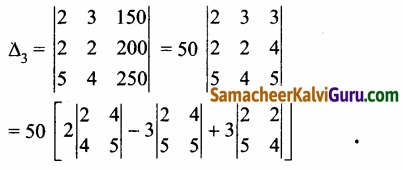
= 50 [2(10 – 16) – 3(10- 20) + 3(8 – 10)]
= 50[2(- 6) – 3(-10) +3(-2)]
= 50 [- 12 + 30 – 6] = 50 [12] = 600.

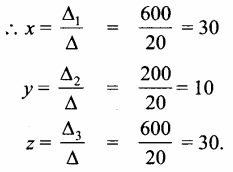
ஆகையால் ஒரு தோசையின் விலை ₹ 30, ஒரு ! இட்லியின் விலை ₹ 10 மற்றும் 1 வடையின் விலை ₹30.
மேலும் 3 தோசைகள், ஆறு இட்லிகள் மற்றும் 6 வடைகளின் விலை
= 3x + 6y + 6z = 3(30) + 6(10) + 6(30)
= 90 + 60 + 180 = ₹330
அக்குடும்பத்தினரிடம் ₹350 இருப்பதால் சாப்பிட்ட செலவிற்கான தொகையை அவர்களிடமிருந்த பணத்தை கொண்டு செலுத்த முடியும்.