Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 12 Introduction to Statistical Methods and Econometrics
It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers. This helps to improve your communication skills.
Samacheer Kalvi 12th Economics Introduction to Statistical Methods and Econometrics Text Book Back Questions and Answers
Part – A
Multiple Choice Questions.
Question 1.
The word ‘statistics’ is used as ………………………
(a) Singular
(b) Plural
(c) Singular and Plural
(d) None of above
Answer:
(c) Singular and Plural
Question 2.
Who stated that statistics as a science of estimates and probabilities?
(a) Horace Secrist
(b) R. A Fisher
(c) Ya-Lun-Chou
(d) Boddington
Answer:
(d) Boddington
Question 3.
Sources of secondary data are …………………………..
(a) Published sources
(b) Unpublished sources
(c) Neither published nor unpublished sources
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)
Question 4.
The data collected by questionnaires are …………………………..
(a) Primary data
(b) Secondary data
(c) Published data
(d) Grouped data
Answer:
(a) Primary data
Question 5.
A measure of the strength of the linear relationship that exists between two variables is called …………………………..
(a) Slope
(b) Intercept
(c) Correlation coefficient
(d) Regression equation
Answer:
(c) Correlation coefficient
Question 6.
If both variables X and Y increase or decrease simultaneously, then the coefficient of correlation will be …………………………..
(a) Positive
(b) Negative
(c) Zero
(d) One
Answer:
(a) Positive
Question 7.
If the points on the scatter diagram indicate that as one variable increases the other variable tends to decrease the value of r will be …………………………..
(a) Perfect positive
(b) Perfect negative
(c) Negative
(d) Zero
Answer:
(c) Negative
Question 8.
The value of the coefficient of correlation r lies between …………………………..
(a) 0 and 1
(b) – 1 and 0
(c) – 1 and + 1
(d) – 0.5 and + 0.5
Answer:
(c) – 1 and + 1
Question 9.
The term regression was used by …………………………..
(a) Newton
(b) Pearson
(c) Spearman
(d) Galton
Answer:
(d) Galton
Question 10.
The purpose of simple linear regression analysis is to …………………………..
(a) Predict one variable from another variable
(b) Replace points on a scatter diagram by a straight-line
(c) Measure the degree to which two variables are linearly associated
(d) Obtain the expected value of the independent random variable for a given value of the dependent variable
Answer:
(a) Predict one variable from another variable
Question 11.
A process by which we estimate the value of dependent variable on the basis of one or more independent variables is called …………………………..
(a) Correlation
(b) Regression
(c) Residual
(d) Slope
Answer:
(b) Regression
Question 12.
If Y = 2 – 0.2X, then the value of Y intercept is equal to …………………………..
(a) -0.2
(b) 2
(c) 0.2X
(d) All of the above
Answer:
(b) 2
Question 13.
In the regression equation Y = β0 + β1 X, the Y is called …………………………..
(a) Independent variable
(b) Dependent variable
(c) Continuous variable
(d) None of the above
Answer:
(b) Dependent variable
Question 14.
In the regression equation X = β0 + β1 X, the X is called …………………………..
(a) Independent variable
(b) Dependent variable
(c) Continuous variable
(d) None of the above
Answer:
(a) Independent variable
Question 15.
Econometrics is the integration of …………………………..
(a) Economics and Statistics
(b) Economics and Mathematics
(c) Economics, Mathematics and Statistics
(d) None of the above
Answer:
(c) Economics, Mathematics and Statistics
Question 16.
Econometric is the word coined by …………………………..
(a) Francis Galton
(b) Ragnar Frish
(c) Karl Person
(d) Spearsman
Answer:
(b) Ragnar Frish
Question 17.
The raw materials of Econometrics are ……………………………
(a) Data
(b) Goods
(c) Statistics
(d) Mathematics
Answer:
(a) Data
Question 18.
The term Uiin regression equation is …………………………..
(a) Residuals
(b) Standard error
(c) Stochastic error term
(d) None
Answer:
(c) Stochastic error term
Question 19.
The term Uiis introduced for the representation of …………………………..
(a) Omitted Variable
(b) Standard error
(c) Bias
(d) Discrete Variable
Answer:
(a) Omitted Variable
Question 20.
Econometrics is the amalgamation of …………………………..
(a) 3 subjects
(b) 4 subjects
(c) 2 subjects
(d) 5 subjects
Answer:
(a) 3 subjects
Part – B
Answer The Following Questions In One or Two Sentences.
Question 21.
What is Statistics?
Answer:
- The term‘Statistics’is used in two senses: as singular and plural.
- In singular form it simply means statistical methods.
- Statistics when used in singular form helps in the collection, presentation, classification and interpretation of data to make it easily comprehensible.
- In its plural form it denotes collection of numerical figures and facts.
- In the narrow sense it has been defined as the science of counting and science of averages.
Question 22.
What are the kinds of Statistics?
Answer:
Types of Statistics:
1. There are two major types of statistics named as Descriptive Statistics and Inferential Statistics.
2. Descriptive Statistics:
The branch of statistics devoted to the summarization and description of data is called Descriptive Statistics.
3. Inferential Statistics:
The branch of statistics concerned with using sample data to make an inference about a population of data is called Inferential Statistics.
Question 23.
What do you mean by Inferential Statistics?
Answer:
Inferential Statistics:
- The branch of statistics concerned with using sample data to make an inference about a population of data is called Inferential Statistics.
- It draws conclusion for the population based on the sample result.
- It uses hypotheses, testing and predicting on the basis of the outcome.
- It tries to understand the population beyond the sample.
Question 24.
What are the kinds of data?
Answer:

Question 25.
Define Correlation?
Answer:
Correlation is a statistical device that helps to analyse the covariation of two or more variables. Sir Francis Galton, is responsible for the calculation of correlation coefficient.
Question 26.
Define Regression?
Answer:
- The term ‘Regression’ was first coined and used in 1877 by Francis Galton while studying the relationship between the height of fathers and sons.
- The average height of children bom of parents of a given height tended to move or “regress” toward the average height in the population as a whole.
- Gabon’s law of universal regression was confirmed by his friend Karl Pearson, who collected more than a thousand records of heights of members of family groups.
- The literal meaning of the word “regression” is “Stepping back towards the average”.
Question 27.
What is Econometrics?
Answer:
Origin Of Econometrics:
- Economists tried to support their ideas with facts and figures in ancient times.
- Irving Fisher is the first person, developed mathematical equation in the quantity theory of money with help of data.
- Ragnar Frisch, a Norwegian economist and statistician named the integration of three subjects such that mathematics, statistical methods and economics as Econometrics” in 1926.
Part – C
Answer The Following Questions In One Paragraph.
Question 28.
What are the functions of Statistics?
Answer:
Functions of Statistics:
- Statistics presents facts in a definite form.
- It simplifies mass of figures.
- It facilitates comparison.
- It helps in formulating and testing.
- It helps in prediction.
- It helps in the formulation of suitable policies.
(I) Statistics are an aggregate of facts:
For example, numbers in a calendar pertaining to a year will not be called statistics, but to be included in statistics it should contain a series of figures with relationships for a prolonged period.
(II) Statistics are numerically enumerated, estimated and expressed.
(III) Statistical collection should be systematic with a predetermined purpose:
The purpose of collection of statistics should be determined beforehand in order to get accurate information.
(IV) Should be capable of being used as a technique for drawing comparison:
It should be capable of drawing comparison between two different sets of data by tools such as averages, ratios, rates, coefficients etc.
Question 29.
Find the Standard Deviation of the following data:
14, 22, 9, 15, 20, 17, 12, 11
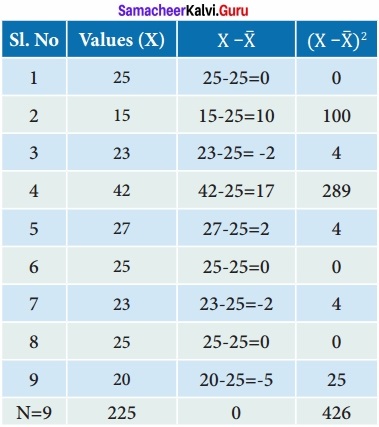

∴ σ = 4.18
Question 30.
State and explain the different kinds of Correlation?
Answer:

Type I:
Based on the direction of change of variables:
Correlation is classified into two types as Positive correlation and Negative Correlation based on the direction of change of the variables.
Positive Correlation:
The correlation is said to be positive if the values of two variables move in the same direction.
Ex 1:
If income and Expenditure of a Household may be increasing or decreasing simultaneously. If so, there is positive correlation. Ex. Y = a + bx
Negative Correlation:
The Correlation is said to be negative when the values of variables move in the opposite directions. Ex. Y = a – bx
Ex 1:
Price and demand for a commodity move in the opposite direction.
Type II:
Based upon the number of variables studied
There are three types based upon the number of variables studied as
- Simple Correlation
- Multiple Correlation
- Partial Correlation
Simple Correlation:
If only two variables are taken for study then it is said to be simple correlation. Ex. Y = a + bx
Multiple Correlations:
If three or more than three variables are studied simultaneously, then it is termed as multiple correlation.
Ex: Determinants of Quantity demanded
Qd = f (P, Pc, Ps, t, y)
Where Qd stands for Quantity demanded, f stands for function.
P is the price of the goods,
Pc is the price of competitive goods
Ps is the price of substituting goods
t is the taste and preference
y is the income.
Partial Correlation:
If there are more than two variables but only two variables are considered keeping the other variables constant, then the correlation is said to be Partial Correlation.
Type III: Based upon the constancy of the ratio of change between the variables
Correlation is divided into two types as linear correlation and Non – Linear correlation based upon the Constancy of the ratio of change between the variables.
Linear Correlation:
Correlation is said to be linear when the amount of change in one variable tends to bear a constant ratio to the amount of change in the other.
Ex. Y = a + bx
Non Linear:
The correlation would be non-linear if the amount of change in one variable does not bear a constant ratio to the amount of change in the other variables.
Ex. Y = a + bx2
Question 31.
Mention the uses of Regression Analysis?
Answer:
Use of Regression Analysis:
- Regression means going back and it is a mathematical measure showing the average relationship between two variables.
- Both the variables may be random variables.
- It indicates the cause and effect relationship between the variables and establishes functional relationship.
- Besides verification it is used for the prediction of one value, in relation to the other given value.
- Regression coefficient is an absolute figure. If we know the value of the independent variable, we can find the value of the dependent variable.
- In regression there is no such spurious regression.
- It has wider application, as it studies linear and nonlinear relationship between the variables.
- It is widely used for further mathematical treatment.
Question 32.
Specify the objectives of econometrics?
Answer:
Objectives of Econometrics:
The general objective of Econometrics is to give empirical content to economic theory. The specific objectives are as follows:
- It helps to explain the behaviour of a forthcoming period that is forecasting economic phenomena.
- It helps to prove the old and established relationships among the variables or between the variables
- It helps to establish new theories and new relationships.
- It helps to test the hypotheses and estimation of the parameter.
Question 33.
Differentiate the economic model with econometric model?
Answer:
Economic Model:
- Economic model is the theoretical construct that represents the complex economic process.
- Economic model is based on mathematical modeling.
- Economic model is focused on establishing the logical relationships between the variables in the model.
- Economic model is applied in stating the theoretical relationship into mathematical equations.
- Economic model believes that outcome is certain and exact. So disturbance term is not required.
- Economic model is deterministic in nature.
- The Keynesian consumption function: C = a + by is the economic model
Econometric Model:
- Econometric model is the statistical concept that represents the numerical estimate of the variables involved in economic process.
- Econometric model is based on statistical modeling.
- Econometric model is focused on estimating the magnitude and direction of relationship between the variables.
- Econometric model is applied in stating the empirical extent of the economic model.
- Econometric model believes that outcome is certain but not exact. So disturbance term plays the vital role.
- Econometric model is stochastic in nature.
- The Keynesian consumption function: C = a + by + µ is the econometric model
Question 34.
Discuss the important statistical organizations (offices) in India?
Answer:
- Official Statistics are statistics published by government agencies or other public bodies such as international organizations.
- They provide quantitative or qualitative information on all major areas of citizens’ lives.
- Official Statistics make information on economic and social development accessible to the public, allowing the impact of government policies to be assessed, thus improving accountability.
- The Ministry of Statistics and Programme Implementation (MOSPI) came into existence as an Independent Ministry in 1999 after the merging of the Department of Statistics and the Department of Programme Implementation.
- The Ministry has two wings, Statistics and Programme Implementation.
National Sample Survey Organisation (NSSO):
- The National Sample Survey Organisation, now known as National Sample Survey Office, is an organization under the Ministry of Statistic of the Government of India.
- It is the largest organisation in India, conducting regular socio-economic surveys.
- It was established in 1950. NSSO has four divisions:
- Survey Design and Research Division (SDRD)
- Field Operations Division (FOD)
- Data Processing Division (DPD)
- Co-ordination and Publication Division (CPD)
The Programme Implementation Wing has three Divisions, namely,
- Twenty Point Programme
- Infrastructure Monitoring and Project Monitoring
- Member of Parliament Local Area Development Scheme.
Besides these three wings, there is National Statistical Commission created through a Resolution of Government of India (MOSPI) and one autonomous Institute, viz., Indian Statistical Institute declared as an institute of National importance by an Act of Parliament.
Part – D
Answer The Following Questions.
Question 35.
Elucidate the nature and scope of Statistics?
Nature of Statistics:
- Different Statisticians and Economists differ in views about the nature of statistics, some call it a science and some say it is an art.
- Tipett on the other hand considers Statistics both as a science as well as an art.
Scope of Statistics:
Statistics is applied in every sphere of human activity – social as well as physical – like Biology, Commerce, Education, Planning, Business Management, Information Technology, etc.
Statistics and Economics:
- Statistical data and techniques are immensely useful in solving many economic problems
- Such as fluctuation in wages, prices, production, distribution of income and wealth and so on.
Statistics and Firms:
Statistics is widely used in many firms to find whether the product is conforming to specifications or not.
Statistics and Commerce:
- Statistics are life blood of successful commerce.
- Market survey plays an important role to exhibit the present conditions and to forecast the likely changes in future.
Statistics and Education:
- Statistics is necessary for the formulation of policies to start new course, according to the changing environment.
- There are many educational institutions owned by public and private engaged in research and development work to test the past knowledge and evolve new knowledge.
- These are possible only through statistics.
Statistics and Planning:
1. Statistics is indispensable in planning. In the modem world, which can be termed as the “world of planning”, almost all the organisations in the government are seeking the help of planning for efficient working, for the formulation of policy decisions and execution of the same.
2. In order to achieve the above goals, various advanced statistical techniques are used for processing, analyzing and interpreting data.
3. In India, statistics play an important role in planning, both at the central and state government levels, but the quality of data highly unscientific.
Statistics and Medicine:
- In Medical sciences, statistical tools are widely used. In order to test the efficiency of a new drug or to compare the efficiency of two drugs or two medicines, t – test for the two samples is used.
- More and more applications of statistics are at present used in clinical investigation.
Statistics and Modern applications:
- Recent developments in the fields of computer and information technology have enabled statistics to integrate their models and thus make statistics a part of decision making procedures of many organisations.
- There are many software packages available for solving simulation problems.
Question 36.
Calculate the Karl Pearson Correlation Co-efficient for the following data?
Answer:


Question 37.
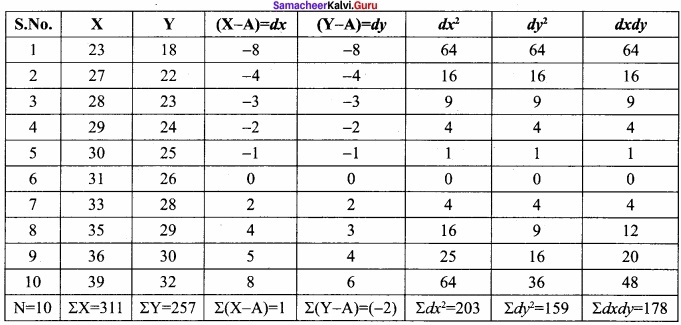
Find the regression equation Y on X and X on Y for the following data?
Answer:



= \(\frac { 16810 }{ 17250-225 } \) = 1.01
X on Y
X – \(\bar { X } \) = bXy (Y – \(\bar { Y } \) )
X – 43.5 = 1.01 (Y – 64.5)
X – 43.5 = 1.01 Y – 65.145 [64.5 × 1.01]
X – 43.5 = 1.01 Y – 65.145
X – 43.5 = 0.01 Y – [65.145 – 43.5]
X = 0.01 Y – 21.645
Question 38.
Describe the application of Econometrics in Economics?
Answer:
Origin Of Econometrics:
- Economists tried to support their ideas with facts and figures in ancient times.
- Irving Fisher is the first person, developed mathematical equation in the quantity theory of money with help of data.
- Ragnar Frisch, a Norwegian economist and statistician named the integration of three subjects such that mathematics, statistical methods and economics as Econometrics” in 1926. Ragnar Anton Kittil Frisch Noble Memorial Prize in 1969.
- The term econometrics is formed from two words of Greek origin, ‘oukovouia’ meaning economy and ‘uetpov’ meaning measure. Econometrics emerged as an independent discipline studying economics phenomena.
- Econometrics may be considered as the integration of economics, Statistics and Mathematics.
- Econometrics is an amalgamation of three subjects which can be easily understood by following Venn diagram and picture representation.
- Economics + Mathematics = Mathematical Economics
- Mathematical Economics + Statistical Data & Its Technique = Econometrics
- {Economics + Statistics + Mathematics} + Empirical Data = Econometrics
Definitions:
- In the words of Arthur S. Goldberger, “Econometrics may be defined as the social science in which the tools of economic theory, mathematics and statistical inference are applied to the analysis of economic phenomena”.
- Gerhard Tinbergen points out that “Econometrics, as a result of certain outlook on the role of economics, consists of application of mathematical statistics to economic data to lend empirical support to the models constructed by mathematical economics and to obtain numerical results”.
- H Theil“Econometrics is concerned with the empirical determination of economic laws”
- In the words of Ragnar Frisch “The mutual penetration of quantitative econometric theory and statistical observation is the essence of econometrics”.
- Econometrics means economic measurement. Econometrics deals with the measurement of economic relationships.

Objectives Of Econometrics:
The general objective of Econometrics is to give empirical content to economic theory. The specific objectives are as follows:
- It helps to explain the behaviour of a forthcoming period that is forecasting economic phenomena.
- It helps to prove the old and established relationships among the variables or between the variables
- It helps to establish new theories and new relationships.
- It helps to test the hypotheses and estimation of the parameter.
Samacheer Kalvi 12th Economics Introduction to Statistical Methods and Econometrics Additional Questions and Answers
Part – A
I. Multiple Choice Questions.
Question 1.
The term statistics originated in the Latin word known as ………………………….
(a) Statistik
(b) Status
(c) Statisque
(d) Statistics
Answer:
(b) Status
Question 2.
The fundamental principles of statistics were developed by the biologist ………………………….
(a) Ronald Fisher
(b) Gottfried Achenwall
(c) R.A. Fisher
(d) GR Neison
Answer:
(a) Ronald Fisher
Question 3.
The first book to have statistics as its title was ………………………….
(a) Contributions to vital statistics
(b) Principles of statistics
(c) Statistics principles
(d) Statistics probabilities
Answer:
(a) Contributions to vital statistics
Question 4.
The subjects of statistics can be attributed to ………………………….
(a) Francis GP. Neison
(b) Ronald Fisher
(c) Gottfried Achenwall
(d) R.A. Fisher
Answer:
(d) R.A. Fisher
Question 5.
To prepare a systematic study of birth and death related data is called ………………………….
(a) Principles of statistics
(b) Contributions of vital statistics
(c) Subject of statistics
(d) Statistics evolution
Answer:
(b) Contributions of vital statistics
Question 6.
Who is the father of statistics?
(a) Gottfried Achenwall
(b) Francis GP. Neison
(c) Ronald Fisher
(d) R.A. Fisher
Answer:
(d) R.A. Fisher
Question 7.
…………………………. form helps in the collection, presentation, classificationandinterpretation of data make it easily comprehensible.
(a) Singular form
(b) Plural form
(c) Collection form
(d) Presentation form
Answer:
(a) Singular form
Question 8.
Statistics is applied in every sphere of ………………………….
(a) Physical activity
(b) Human activity
(c) Maths activity
(d) Statistics activity
Answer:
(b) Human activity
Question 9.
Statistical data and techniques are immensely useful in solving many …………………………. problems.
(a) Statistical
(b) Technical
(c) Economic
(d) Maths
Answer:
(c) Economic
Question 10.
Statistics are life blood of successful ………………………….
(a) Maths
(b) Datas
(c) Calculations
(d) Commerce
Answer:
(d) Commerce
Question 11.
In the modem world, which can be termed as the “World of planning”?
(a) Statistics
(b) Datas
(c) Numerical data
(d) Five year plan
Answer:
(a) Statistics
Question 12.
Since 2007, 29th June every year is celebrated as …………………………
(a) Economic day
(b) Datas day
(c) Statistics day
(d) Planning day
Answer:
(c) Statistics day
Question 13.
In India, statistics play an important role of planning, both at the central and ……………………….. government levels.
(a) State
(b) Local
(c) District
(d) National
Answer:
(a) State
Question 14.
Statistical tools are widely used in …………………………..
(a) Statistical science
(b) Technical science
(c) Medical science
(d) Engineering science
Answer:
(c) Medical science
Question 15.
The branch of statistics devoted to the summerization and description of data is called ………………………… statistics.
(a) Descriptive
(b) Inferential
(c) Qualitative
(d) Quantitative
Answer:
(a) Descriptive
Question 16.
The branch of statistics concerned with using sample data is called ……………………… statistics.
(a) Descriptive
(b) Qualitative
(c) Descriptive
(d) Inferential
Answer:
(d) Inferential
Question 17.
…………………………. are those that can be quantified in definite units of measurement
(a) Quantitative
(b) Qualitative
(c) Descriptive
(d) Inferential
Answer:
(a) Quantitative
Question 18.
……………………….. is called a measure of central tendency or an average or a measure of location.
(a) Arithmetic mean
(b) Mean
(c) Cental value
(d) Geometric mean
Answer:
(c) Cental value
Question 19.
…………………….. is one of the methods of Absolute measure of dispersion.
(a) Standard Deviation
(b) Arithmetic mean
(c) Mean
(d) Median
Answer:
(a) Standard Deviation
Question 20.
…………………… is a statistical device that helps to analyse the covariation of two or more variables.
(a) Deviation
(b) Standard deviation
(c) Correlation
(d) Median
Answer:
(c) Correlation
Question 21.
………………………. Method is very simple and non-mathematical method.
(a) Scatter Diagram
(b) Graphic
(c) Karl Pearson’s
(d) Actual mean
Answer:
(a) Scatter Diagram
Question 22.
The literal meaning of the word “Regression” is stepping back towards the …………………………….
(a) Standard deviation
(b) Mean deviation
(c) Average
(d) Median
Answer:
(c) Average
Question 23.
…………………………. may be considered as the integration of economics, statistics and mathematics.
(a) Mathematical economics
(b) Statistical economics
(c) Technic economics
(d) Econometrics
Answer:
(d) Econometrics
Question 24.
The Central statistical office is one of the two – wings of the …………………………
(a) State statistical organisation
(b) National statistical organisation
(c) District statistical organisation
(d) World statistical organisation
Answer:
(b) National statistical organisation
II. Match The Following And Choose The Correct Answer By Using Codes Given Below.
Question 1.
A. Galton – (i) Principle of statistics
B. Ragnar Frisch – (ii) Regression
C. P.C. Mohalanobis – (iii) Econometrics
D. Ronald Fisher – (iv) Modem Statistics
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C (iv) D(i)
(c) A (iii) B (iv) C (i) D (ii)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(b) A (ii) B (iii) C (iv) D(i)
Question 2.
A. Statistics – (i) Solving economic problems
B. Statistical data – (ii) Successful commerce
C. Statistical tools – (iii) World of planning
D. Statistics life blood – (iv) Medical science
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (iv) B (iii) C (ii) D(i)
Answer:
(c) A (iii) B (i) C (iv) D (ii)
Question 3.
A. Types of statistics – (i) Central value
B. Statistics data categories – (ii) Primary data
C. Collection of data – (iii) Central value
D. Measure of central tendency – (iv) Descriptive statistics
Codes:
(a) A (i) B (ii) C (ii) D (iv)
(b) A (iv) B (iii) C (ii) D(i)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (ii) B (iv) C (i) D (iii)
Answer:
(b) A (iv) B (iii) C (ii) D(i)
Question 4.
A. Karl Pearson – (i) Regression
B. Measures of dispersion – (ii) Standard Deviation
C. Sir. Francis Galton – (iii) Absolute
D. Stepping back towards the average – (iv) Correlation
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D(i)
Answer:
(d) A (ii) B (iii) C (iv) D(i)
Question 5.
A. NSSO – (i) 1999
B. MOSPI – (ii) 1877
C. Francis Galton – (iii) 1890 – 1962
D. R.A. Fisher – (iv) 1950
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(c) A (iv) B (i) C (ii) D (iii)
Question 6.
A. Francis GP. Neison – (i) England
B. Gottfried Achenwall – (ii) Contributions to vital statistics
C. Ronald Fisher – (iii) P.C. Mahalanobis
D. Modem statistics – (iv) Statistik
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (i) C (iv) D (ii)
(c) A (ii) B (iv) C (i) D (iii)
(d) A (iv) B (iii) C (ii) D(i)
Answer:
(c) A (ii) B (iv) C (i) D (iii)
III. Choose The Correct Statement:
Question 1.
(i) Statistics is indispensable planning.
(ii) In the modem world, it can be termed as the “World of planning”.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true
Question 2.
(i) Statistical data and techniques are immensely useful in solving many economic problems.
(ii) Fluctuation in Inflation, Deflation.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false
Question 3.
(i) Quantitative data are those that can be quantified in definite units of measurement.
(ii) These refer to characteristics in successive measurements yield quantifiable observations.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true
Question 4.
(i) Karl Pearson introduced the concept of Standard deviation.
(ii) Standard Deviation is one of the methods of Relative measure of dispersion.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false
Question 5.
(i) The term econometrics is formed from two words of Greek origin, ‘Oukovovia’ meaning economy and ‘vetpov’ meaning measure.
(ii) Econometrics may be considered as integration of economics, statistics and mathematics.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true
IV. Which of The Following Is Correctly Matched.
Question 1.
(a) Gottfried Achenwall – Statistics
(b) GP. Neison – Contributions to vital statistics
(c) Ronald Fisher – Movemental contribution
(d) Modem statistics – Ronald Fisher
Answer:
(b) GP. Neison – Contributions to vital statistics
Question 2.
(a) Quantitative data – Gender, community
(b) Qualitative data – Age, income
(c) Nominal data – Classification of students
(d) Rank data – Collection of data
Answer:
(c) Nominal data – Classification of students
Question 3.
(a) Central value – Measure of central tendency
(b) Dispersion – Average
(c) Standard Deviation – Ronald Fisher
(d) Sir Francis Galton – Graphic Method
Answer:
(a) Central value – Measure of central tendency
Question 4.
(a) Francis Galton – Stepping back towards the average
(b) Irving Fisher – Data
(c) Ragner Frisch – Technique
(d) Econometrics – Economy + Metrics
Answer:
(a) Francis Galton – Stepping back towards the average
Question 5.
(a) Arthur S. Gold Berger – Maths
(b) Gerherd Tinbergen – Social
(c) H. Theil – Economic laws
(d) Ragnar Frisch – Statistics
Answer:
(c) H. Theil – Economic laws
V. Which of The Following is Not Correctly Matched.
Question 1.
(a) Statistic Regression – Y1 = β0 + β1X1
(b) Econometrics Regression – Y1 = β0 + β1X1 + U1
(c) Regression lines – X on Y ⇒ X = a + by
(d) Actual Mean Method = \(\frac { \Sigma X }{ N } \)
Answer:
(d) Actual Mean Method = \(\frac { \Sigma X }{ N } \)
Question 2.
(a) SDRD – Survey Design and Research Division
(b) FOD – Field Operations Division
(c) DPD – Division Processing Data
(d) CPD – Co – Operation and Publication Division
Answer:
(c) DPD – Division Processing Data
Question 3.
(a) NSO – National Statistical Office
(b) CSO – Cental Statistical Office
(c) NSSO – National Sample Survey Organisation
(d) NAD – National Arithematic Division
Answer:
(d) NAD – National Arithematic Division
Question 4.
(a) NAD – National Accounts Division
(b) SSD – Social Stastistics Division
(c) ESD – Economic Social Division
(d) TD – Training Division
Answer:
(c) ESD – Economic Social Division
Question 5.

Answer:

VI. Pick The Odd One Out.
Question 1.
Functions of Statistics
(a) Statistics presents facts in a definite form
(b) It simplifies mass of figures
(c) It helps firms
(d) It helps in formulating and testing
Answer:
(c) It helps firms
Question 2.
Based upon the number of variables studied as
(a) Simple correlation
(b) Multiple correlation
(c) Partial correlation
(d) Linear correlation
Answer:
(d) Linear correlation
Question 3.
Methods of studying correlation
(a) Scatter diagram method
(b) Graphic method
(c) Maths method
(d) Method of least squares
Answer:
(c) Maths method
Question 4.
NSSO divisions are
(a) Survey Design and Research Division [SDRD]
(b) Fashion Operation Division [FOD]
(c) Data Processing Division [DPD]
(d) Co – ordination and Publication Division [CPD]
Answer:
(b) Fashion Operation Division [FOD]
Question 5.
CSO Director Generals are
(a) National Accounts Division [NAD]
(b) Sample Statistics Division [SSD]
(c) Economic Statistics Division [ESD]
(d) Co – ordination and Publication Division [CPD]
Answer:
(b) Sample Statistics Division [SSD]
VII. Assertion and Reason.
Question 1.
Assertion (A): The monumental contribution to the subject of statistics can be attributed to R.A. Fisher was able to apply statistics to a variety.
Reason (R): Fields such as Biometry, Genetics, Psychology, Education, Agriculture and others.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
Question 2.
Assertion (A): In singular form it simply means simple method.
Reason (R): Singular forms help in the collection, presentation, classification and interpretation of data.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true
Question 3.
Assertion (A): Statistics is indispensable in planning.
Reason (R): In the modem world, which can be termed as the “World of Planning” almost all organisations.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
Question 4.
Assertion (A): Quantitative data are those that can be quantified in definite units of measurement.
Reason (R): These refer to characteristics of a subject or an object.
(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are tme but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false
Question 5.
Assertion (A): Ronald Fisher introduced the concept of Standard Deviation.
Reason (R): Standard Deviation is one of the methods of Absolute measure of dispersion.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true
Part – B
Answer The Following Questions In One or Two Sentences.
Question 1.
Write five averages?
Answer:
- There are five averages.
- Among them mean, median and mode are called simple averages and the other two averages geometric mean and harmonic mean are called special averages.
Question 2.
Write meaning of averages?
Answer:
- “A measure of central tendency is a typical value around which other figures congregate.”
- “An average stands for the whole group of which it forms a part yet represents the whole.”
- “One of the most widely used set of summary figures is known as measures of location.”
Question 3.
Write the kinds of dispersion?
Answer:
There are two kinds of measures of dispersion, namely
- Absolute measure of dispersion
- Relative measure of dispersion
Question 4.
Explain the calculation of standard deviation individual series?
Answer:
Calculation of Standard deviation-individual Series:
There are two methods of calculating Standard deviation in an individual series.
(a) Deviations taken from Actual mean
(b) Deviation taken from Assumed mean
Standard Deviation = 
Where, \(\bar { X } \) = mean value of distribution
n = number of observations
Question 5.
Write the four methods of studying correlation?
Answer:
Methods of Studying Correlation:
The various methods of ascertaining whether two variables are correlated or not are:
- Scatter diagram Method
- Graphic Method
- Karl Pearson’s Co-efficient of correlation and
- Method of Least Squares.
Question 6.
Explain the advantages of Scatter diagram method?
Answer:
Advantages of Scatter Diagram method:
- It is very simple and non- mathematical method
- It is not influenced by the size of extreme item.
- It is the first step in resting the relationship between two variables.
Question 7.
Write the two regression lines?
Answer:
Two Regression lines:
X on Y => X = a + by
Y on X => Y = a + bx
Question 8.
Write flow chart of Anatomy/Methodology of Econometrics?
Answer:
Flow Chart of Anatomy / Methodology of Econometrics:
Anatomy of Econometric Modeling

Question 9.
Explain the statistics and econometrics regression equations?
Answer:
Statistics Regression:
Yi = β0 + β1X1
Econometrics Regression:
Yi = β0 + β1Xi + Ui
(with more than 2 variables) or
Y = β0 + β1X1 + β2X2 + β3X3 + Ui
- Systematic Part: β0 + β1X1 or explained part and Random Part: Uf unexplained part in a regression.
- Ui represents the role of omitted variables in specifying a regression relationship of Y on X.
- Hence, the Ui cannot and should not be ignored.
Part – C
Answer The Following Questions In One Paragraph.
Question 1.
Explain the sources of collection of data?
Answer:
Sources of Collection of data:
Based on the data sources, data could be seen as of two types, viz., secondary data and primary data. The two can be defined as under:
(I) Primary data:
- Those data which do not already exist in any form, and thus have to be collected for the first time from the primary source(s).
- By their very nature, these data are fresh and first-time collected covering the whole population or a sample drawn from it.
(II) Secondary data:
- They already exist in some form: published or unpublished in an identifiable secondary source.
- They are, generally, available from published source(s), though not necessarily in the form actually required, e.g. Data from CSO, NSSO, RBI….
Question 2.
Briefly explain the kinds of measures of dispersion?
Answer:
There are two kinds of measures of dispersion, namely
- Absolute measure of dispersion
- Relative measure of dispersion
Absolute measure of dispersion indicates the amount of variation in a set of values in terms of units of observations. Relative measures of dispersion are free from the units of measurements of the observations. They are pure numbers. They are used to compare the variation in two or more sets, which are having different units of measurements of observations. Standard Deviation is one of the methods of Absolute measure of dispersion.
Karl Pearson introduced the concept of standard deviation in 1893. Standard deviation is also called Root- Mean Square Deviation. The reason is that it is the square – root of the mean of the squared deviation from the arithmetic mean. It provides accurate result. Square of standard deviation is called Variance.
Question 3.
Briefly explain the calculation of standard deviation individual series steps?
Answer:
Steps:
- Find out the actual mean of given data ( \(\bar { X } \) )
- Find out the deviation of each value from the mean (x = X – \(\bar { X } \) )
- Square the deviations and take the total of squared deviations Σx2
- Divided the total Σx2 by the number of observation ( \(\frac { \Sigma x^{ 2 } }{ n } \) )
- The square root of ( \(\frac { \Sigma x^{ 2 } }{ n } \) ) is standard deviation.

\(\frac { \Sigma x^{ 2 } }{ n } \) = Variance = \(\frac { \Sigma (x-\bar { x } )^{ 2 } }{ n } \)
When the sample size is less than 30, variance = \(\frac { \Sigma (x-\bar { x } )^{ 2 } }{ n-1 } \)
When n = number of observations.
Question 4.
Calculate the standard deviation from the following data by Actual Mean Method?
125, 15, 23, 42, 27, 25, 23, 25 and 20
Solution:
Deviations from actual mean.

\(\bar { X } \) = \(\frac{225}{9}\) = 25

σ = 6.88
Question 5.
Calculate the standard deviation for the following data by assumed mean method?
[43, 48, 65, 57, 31, 60, 37, 48, 78, 59]
Solution:
Deviation from assumed mean

Question 6.
Write the assumptions of the Linear Regression Model?
Answer:
Assumptions of the Linear Regression Model:
The Linear regression model is based on certain assumptions
- Some of them refer to the distribution of the random variable .
- Some of them refer to the relationship between Ui and the explanatory variables (x1, x2, x3 given in the above example).
- Some of them refer to the relationship between Ui the explanatory variables themselves.
Part – D
Answer The Following Questions In About A Page.
Question 1.
Explain the Scatter Diagram Method. Advantages and Disadvantages with diagram?
Answer:
Scatter Diagram Method:
- Scatter diagram is a graph of observed plotted points where each point represents the values of X and Y as a coordinate.
- It portrays the relationship between these two variables graphically.
Advantages of Scatter Diagram method:
- It is very simple and non- mathematical method
- It is not influenced by the size of extreme item.
- It is the first step in resting the relationship between two variables.
Disadvantages of Scatter diagram method:
- It cannot establish the exact degree of correlation between the variables, but provides direction of correlation and depicts it is high or low.

Question 2.
Briefly explain Karl Pearson’s co-effecient of correlation?
Answer:
Karl Pearson’s Coefficient of Correlation:
- Karl Pearson’s Method is popularly known as Pearson’s coefficient of correlation denoted by the symbol V.
- The coefficient of correlation V measures the degree of linear relationship between two variables say X and Y.
- The Formula for computing Karl Pearson’s Coefficient of correlation is:
(I)

‘r’ is caluculated by Direct Method without taking deviation of terms either from actual mean or assumed mean.
(II) r is calculated by taking the Deviation from actual mean.

(III) ‘r’ is caluculated by taking assumed mean

Where dx refers to deviations ofx series from assumed mean (x – \(\bar { x } \) ), dy refers to deviations of y series from an assumed mean of (y – \(\bar { y } \) )
Σdxdy = Sum of product of the deviations x and y series from their assumed means.
Σdx2 = Sum of the squares of the deviation of x series from an assumed mean
Σdy2 = Sum of the squares of the deviations of y series from an assumed mean
Σdx = Sum of the deviation of x series from an assumed mean of x
Σdy = Sum of the deviation of y series from an assumed mean of y
Question 3.
Explain the procedure for computing the correlation co – effecient for direct and deviation from actual mean method steps?
Answer:
Procedure for Computing the Correlation Coefficient: (For Direct and Deviation from actual mean method).
- Step – 1 Calculate the mean of two series ‘X’ ‘Y’
- Step – 2 Calculate the deviations ‘X’ and Y in two series from their respective mean.
- Step – 3 Square each deviations of ‘X’ and ‘ Y’ then obtain the sum of the Squared deviation
- Step – 4 Multiply each deviation under X with each deviation under Y and obtain the product of ‘xy’. Then obtain the sum of the product of X, Y. Then obtain the sum of the product of x, y is Σxy.
- Step – 5 Substitute the value in the formula.
Question 4.
State the formula of Karl Pearson’s co – effecient of correlation upgrouped data?

1. Direct Method:
(I)

(II) Assumed Mean Deviation Method

2. Indirect Method:
dx = (x – \(\bar { x } \) ) and dy = (y – \(\bar { y } \) )
r is free from origin
r is free from unit of measurement -1 ≤ r ≤ + 1
Question 5.
Calculate Karl Pearson’s Coefficient of correlation from the following data and interpret its value:

Solution: Let us take Price as X and supply as Y
Computation of Pearson’s Correlation Coefficient:



Price of the product and supply for the product is positively correlated. When price of the product increases then the supply for the product also increases.
Question 6.
Estimate the coefficient of correlation with actualmean method for the following data?

Solution:


Applying in Formula

r = 0.327, The Car is getting old in years the cost of maintainance is also increasing. The age of Car and its maintainance are positively correlated.
Question 7.
Find the Karl Pearson coefficient of Correlation between X and Y from the following data:

Solution:
Formula for Assumed Mean Deviation method.



Take the assumed values A = 16 & B = 27 therefore dx = X – A ⇒ X – 16 and
dy = Y – A ⇒ Y = 27

There exists a positive high correlation between X and Y.
Question 8.
Explain the difference between correlation and regression?
Answer:
Difference between Correlation and Regression:
Correlation:
- Correlation is the relationship between two or more variables, which vary with the other in the same or the opposite direction.
- Both the variables X and Y are random variables.
- It finds out the degree of relationship between two variables and not the cause and effect relationship.
- It is used for testing and verifying the relation between two variables and gives limited information.
- The coefficient of correlation is a relative measure. The range of relationship lies between -1 and +1.
- There may be spurious correlation between two variables.
- It has limited application, because it is confined only to linear relationship between the variables.
- It is not very useful for further mathematical treatment.
Regression:
- Regression means going back and it is a mathematical measure showing the average relationship between two variables.
- Both the variables may be random variables.
- It indicates the cause and effect relationship between the variables and establishes functional relationship.
- Besides verification it is used for the prediction of one value, in relation to the other given value.
- Regression coefficient is an absolute figure. If we know the value of the independent variable, we can find the value of the dependent variable.
- In regression there is no such spurious regression.
- It has wider application, as it studies linear and nonlinear relationship between the variables.
- It is widely used for further mathematical treatment.
Question 9.
Explain Fit the Regression equation on [X on Y]?
Answer:
Fit regression equation X on Y and Y on X for the following data.
\(\bar { X } \) = 12, \(\bar { Y } \) = 10, σy = 0.2, σx = 0.1 and r = 0.85
Solution:
The regression X on Y is
(X – \(\bar { X } \) ) r = r × \(\frac{σx}{σy}\) × (X – \(\bar { X } \) )
Given \(\bar { X } \) = 12, \(\bar { Y } \) = 10
r = 0.85, σx = 0.1 and σy = 0.2
Then substituting the values in formula
(X – 12) = 0.85 × (0.1/0.2) × (Y – 10)
(X – 12) = 0.85 × (0.5) × (Y – 10)
X = 0.425 × (Y – 10) + 12
X = 0.425 Y – 4.25 + 12
X = 0.425 Y + 7.75
Y on X
Y = 0.425 Y + 7.75
Question 10.
Explain Fit the Regression equation on [Y on X]?
Answer:
The regression Y on X is
(Y – \(\bar { Y } \) ) r = r × \(\frac{σx}{σy}\) × (X – \(\bar { X } \) )
Given \(\bar { X } \) = 12, \(\bar { Y } \) = 10
r = 0.85, σx = 0.1 and σy = 0.2
Then substituting the values in formula
(Y – 10) = 0.85 × (0.2/0.1) × (X – 12)
(Y – 10) = 0.85 × (2) × (X – 12)
Y = 1.7 × (X – 12) + 10
Y = 1.7 X – 20.4 + 10
Y = 1.7 X – 10.4
Y on X
Y = 1.7 X – 10.4
Question 11.
Briefly explain Methodology of Econometrics?
Answer:
Methodology of Econometrics:
Broadly speaking, traditional or classical econometric methodology consists of the following steps.
- Statement of the theory or hypothesis
- Specification of the mathematical model of the theory
- Specification of the econometric model of the theory
- Obtaining the data
- Estimation of the parameters of the econometric model
- Hypothesis testing
- Forecasting or prediction
- Using the model for control or policy purposes.
Question 12.
Explain the explanatory variables Assumptions?
Answer:
The explanatory variables are called assumptions.
Assumptions:
- “U” is a random real variable. That is “U” may assume positive, negative or zero values. Hence the mean of the “U” will be zero.
- The variance of “U” is constant for all values of “U”
- The “U” has a normal distribution.
- The Covariances of any U. with any other U are equal to zero
- “U” is independent of explanatory variable (s)
- Explanatory variables are measured without error.
- The explanatory variables are not perfectly linearly correlated.
- The variables are correctly aggregated.
- The relationship is correctly identified and specified.
- Parameters are linear.
Question 13.
Explain the flow chart of statistics and programme Implementation of the Ministry wings?
Answer:
The Ministry has two wings, Statistics and Programme Implementation

Share this Tamilnadu State Board 12th Economics Solutions Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.