Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Additional Problems

Students can download 12th Business Maths Chapter 7 Probability Distributions Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Additional Problems

Choose the correct answer:

Question 1.
If X is a poisson variate with P (X = 1) = P (X = 2), the mean of the poisson variate is equal to _____
(a) 1
(b) 2
(c) -2
(d) 3
Answer:
(b) 2
Hint:
P(X = 1) = P(X = 2)

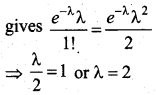
Question 2.
If ‘λ’ is the mean of the Poisson distributions, then P (X = 0) is given by ________
(a) \(e^{-\lambda}\)
(b) \(e^{\lambda}\)
(c) e
(d) \(\lambda^{-e}\)
Answer:
(a) \(e^{-\lambda}\)
Hint:

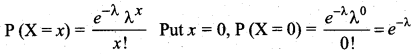
Question 3.
A larger standard deviation for a normal distribution with an unchanged mean indicates that the curve becomes, ____
(a) narrower and more peaked
(b) flatter and wider
(c) more skewed to the right
(d) more skewed to the left
Answer:
(b) flatter and wider

Question 4.
If X ~ N (0, 4), the value of P(|X| ≥ 2.2) is ______
(a) 0.2321
(b) 0.8438
(c) 0.2527
(d) 0.2714
Answer:
(d) 0.2714
Hint:
P (|X| ≥ 2.2)
= P (X > 2.2) + P (X < -2.2)
= P(Z > \(\frac{2.2-0}{2}\)) + P(Z < \(\frac{-2.2-0}{2}\))
= P(Z > 1.1) + P(Z < -1.1)
= 2 P(Z > 1.1) (by symmetry)
= 2[0.5 – P(0 < Z < 1.1)]
= 2 [0.5 – 0.3643]
= 0.2714

Question 5.
For a binomial distribution.

1. If n = 1, then E(X) is ________
2. The variance is always ________
3. Successive trials are ______
4. Negatively skewed when _______
5. Number of parameters is _______
6. n = 10, p = 0.3, variance is _______
7. Is symmetrical when ______
8. n = 6, p = 0.9, P (X = 7) is _______
9. Mean, median and mode will be equal when ______

Answer:

1. p
2. less than mean
3. independent
4. p > \(\frac {1}{2}\)
5. two
6. 2.1
7. p = q
8. zero
9. p = 0.5

Question 6.
For a Normal distribution

1. The parameters which controls the flatness of the curve is _____ & ______
2. If Y = 5X + 10 and X ~ N (10, 25), then mean of Y is _______
3. Normal curve is asymptotic to the ________
4. The median corresponds to the value of Z = _______
5. The area under the normal curve on either side of mean is _______

Answer:

1. µ, σ
2. 60
3. X-axis
4. µ
5. 0.5

Question 7.
Heights of college girls follows a normal distribution with mean 65 inches and a standard deviation of 3 inches. About what proportion of girls are between 65 and 67 inches tall?
(a) 0.75
(b) 0.5
(c) 0.25
(d) 0.17
Answer:
(c) 0.25
Hint:
P (65 < X < 67)
= P(\(\frac{65-65}{3}\) < Z < \(\frac{67-65}{3}\))
= P(0 < Z < 67)
= 0.2486 ~ 0.25

Question 8.
Which one of these is a binomial random variable?
(a) time is taken by a randomly chosen student to complete an exam
(b) number of books bought by a randomly chosen student
(c) number of women taller than 150 cm in a random sample of 10 women
(d) number of CD’s a randomly selected person owns
Answer:
(c) number of women taller than 150 cm in a random sample of 10 women

Question 9.
Pulse rates of adult men follows a normal distribution with a mean of 70 and a standard deviation of 8. Which choice tells how to find the proportion of men that have a pulse rate greater than 78?

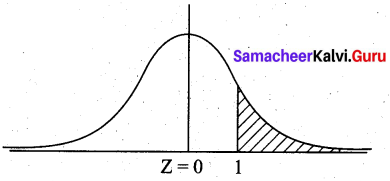
(a) find the area to the left of Z = 1 under the normal curve
(b) find the area between Z = -1 and Z = 1 under the standard normal curve
(c) find the area to the right of Z = 1 under the standard normal curve
(d) find the area to the right of Z = -1 under the standard normal curve
Answer:
(c) find the area to the right of Z = 1 under the standard normal curve
Hint:
P(X > 78) = P(Z > \(\frac{78-70}{8}\)) = P(Z > 1)

2 Mark Questions

Question 1.
The probability that a radio manufactured by a company will be defective is \(\frac{1}{10}\). If 15 such radios are inspected, find the probability that exactly 3 will be defective.
Solution:
Given n = 15, p = \(\frac{1}{10}\) = 0.1, q = 0.9 10
Let X be the binomial variable, denoting the number of radios.
We want probability of exactly 3 defectives, (i.e) P (X = 3)
Now P (X = 3) = \(^{15} \mathrm{C}_{3}(0.1)^{3}(0.9)^{12}\)
= 455 (0.001) [(0.9)⁴]³
= (455) (0.001) (0.6561)³
= 0.1285

Question 2.
The probability that a bulb produced in a factory will fuse after 10 days is 0.05. Find the probability that out of 5 such bulbs, not more than 1 will fuse after 400 days of use.
Solution:
Given that X ~ B (5, 0.05)
(i.e.) n = 5, p = 0.05, q = 0.95
P(X ≤ 1) = P(X = 0) + P(X = 1)
= \(^{5} \mathrm{C}_{0}(0.05)^{0}(0.95)^{5}+^{5} \mathrm{C}_{1}(0.05)^{1}(0.95)^{4}\)
= (0.95)⁵ + 5 (0.05) (0.95)⁴
= (0.95)⁴ + [0.95 + 0.25]
= 0.9774

Question 3.
The number of traffic accidents that occur in a particular road follows a Poisson distribution with a mean of 9.4. Find the probability that less than two accidents will occur on this road during a randomly selected month.
Solution:
Let X be the Poisson variate with mean λ = 9.4.
Now P(X < 2) = P (X = 0) + P (X = 1)
= \(e^{-9.4}\) [1 + 9.4]
= \(e^{-9.4}\) (10.4)
= 0.00086

Question 4.
What is the probability of getting 2 Sundays out of 15 days selected at random?
Solution:

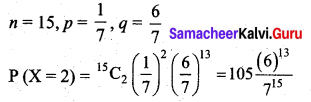
Question 5.
Find the mean and standard deviation of a Poisson variate X which satisfies the condition P(X = 2 ) = P(X = 3)
Solution:
P(X = 2 ) = P(X = 3)
\(\frac{e^{-\lambda} \lambda^{2}}{2 !}=\frac{e^{-\lambda} \lambda^{3}}{3 !}\)
1 = \(\frac{\lambda}{3}\) (or) λ = 3
Variance for Poisson distribution is λ = 3. Hence s.d = √3

Question 6.
Between 5 to 6 p.m., the average number of phone calls per minute is 4. What is the probability that there is no phone call during a minute?
Solution:
Let X be the Poisson variate denoting the number of phone calls per minute.
Given that mean λ = 4. We want P(X = 0)
Now P(X = 0) = \(\frac{e^{-4} \lambda^{0}}{0 !}\) = e^-4 = 0.0183

Question 7.
2% cars are defective. What is the probability that one of 150 cars, there is exactly one defective car?
Solution:
Let X be the Poisson variate denoting the number of defective cars. The mean λ is given by
λ = \(\frac {2}{100}\) × 150 = 3
So P(X = 1) = \(\frac{e^{-3}(3)^{1}}{1 !}\) = 3e^-3 = 0.1494

Question 8.
What is the standard deviation of the number of recoveries among 48 patients, the probability of recovering is 0.75.
Solution:
Given n = 48, p = 0.75, q = 0.25
This is a binomial distribution.
The variance is given by Var (X) = npq
= (48) (0.75) (0.25)
= 9 .
So the standard deviation is √9 = 3

3 and 5 Mark Questions

Question 1.
What is the probability of success of the binomial distribution satisfying the following condition: 4P(X = 4) = P(X = 2) and having other parameter as 6?
Solution:
Given n = 6, 4P(X = 4) = P(X = 2).
We have to find p.

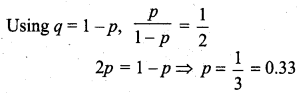
Question 2.
Wool fibre breaking strengths are normally distributed with mean µ = 23.56 and S.D σ = 4.55. What proportion of fibres would have a breaking strength of 14.45 or less?
Solution:

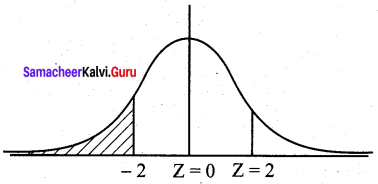
Let X be the normal variable denoting the breaking strengths.
We want to find
P(X ≤ 14.45) = P(Z ≤ \(\frac{14.45-23.56}{4.55}\)) = P(Z ≤ -2.00)
By Symmetry,
P(Z ≤ -2) = P(Z ≥ 2)
= 0.5 – P(0 ≤ Z ≤ 2)
= 0.5 – 0.4772
= 0.0228
Hence the proportion of fibres with a breaking strength of 14.45 or less is 2.28%

Question 3.
The finish times for marathon runners during a race are normally distributed with a mean of 195 minutes and a standard deviation of 25 minutes.
(a) What is the probability that a runner will complete the marathon within 3 hours?
(b) Calculate to the nearest minute, the time by which the first 8% runners have completed the marathon?
(c) What proportion of the runners will complete the marathon between 3 hours and 4 hours?
Solution:
Let X be the normal variate denoting the finish time of the marathon runners.
Given the mean µ = 195 and s.d σ = 25
(a) P(X ≤ 3 hours)
= P(X ≤ 180 minutes)
= P(Z ≤ \(\frac{180-195}{25}\))
= P(Z ≤ -0.6)
By symmetry
P(Z ≤ -0.6)
= P(Z ≤ 0.6)
= 0.5 – P(0 ≤ Z ≤ 0.6)
= 0.5 – 0.2258
= 0.2742
(i.e) Probability of a runner taking less than 3 hours is 0.2742

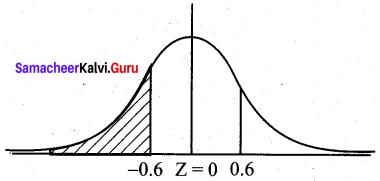
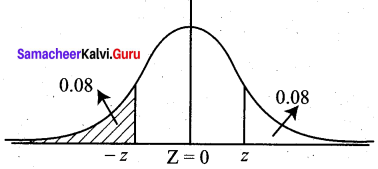
(b) Given the probability is 8% = 0.08
P (Z ≥ z) = 0.08
0.5 – P(0 ≤ Z ≤ z) = 0.08
P(0 ≤ Z ≤ z) = 0.42
z = 1.41 (from normal tables)
Hence \(\frac{X-195}{25}\) = -1.41
X = 25 (-1.41) + 195 = 159.75 = 160 minutes

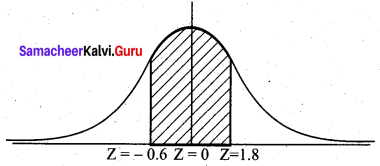
(c) P(3 hours < X < 4 hours)
= P (180 min < X < 240 min)
= P(\(\frac{180-195}{25}\) < Z < \(\frac{240-195}{25}\))
= P(-0.6 < Z < 1.8)
= P (-0.6 < Z < 0) + P (0 < Z < 1.8)
= P(0 < Z < 0.6) + P(0 < Z < 1.8)
= 0.2258 + 0.4641
= 0.6899
Hence the proportion of runners taking between 3 hours and 4 hours is 68.99%

Question 4.
The probability that a driver must stop at any one traffic light is 0.2. There are 15 sets of traffic lights on the journey.
(а) What is the probability that a student must stop at exactly 2 of the 15 sets of traffic lights?
(b) What is the probability that a student will be stopped at 1 or more of the 15 sets of traffic lights?
Solution:
Let X be the binomial random variable denoting the number of traffic lights.
Given n = 15, p =0.2, q = 0.8

Question 5.
A radioactive source emits 4 particles on average during a five-second period.
(а) Calculate the probability that it emits 3 particles during a five-second period.
(b) Find the probability that it emits at least one particle during a 5 second period.
(c) During a 10 second period, what is the probability that 6 particles are emitted?
Solution:
Let X be the Poisson variable denoting the number of particles emitted.
Given the mean λ = 4

Question 6.
Given that X ~ B (n, p) and E(X) = 24, Var(X) = 8, find the values of n and p.
Solution:
We know E(X) = np = 24 and Var(X) = npq = 8

Question 7.
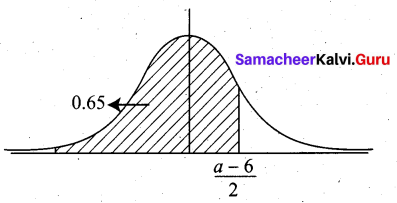
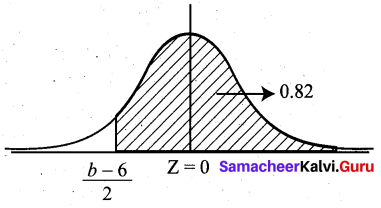
Given that X ~ N (6, 4), find the values of ‘a’ and ‘b’ such that P (X ≤ a) = 0.6500 and P(X ≤ b) = 0.8200
Solution: