Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.5

Students can download 12th Business Maths Chapter 4 Differential Equations Ex 4.5 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.5

Solve the following differential equations:

Question 1.
\(\frac{d^{2} y}{d x^{2}}-6 \frac{d y}{d x}+8 y=0\)
Solution:
Given (D² – 6D + 8) y = 0, D = \(\frac{d}{d x}\)
The auxiliary equations is
m² – 6m + 8 = 0
(m – 4)(m – 2) = 0
m = 4, 2
Roots are real and different
The complementary function (C.F) is (Ae^4x + Be^2x)
The general solution is y = Ae^4x + Be^2x

Question 2.
\(\frac{d^{2} y}{d x^{2}}-4 \frac{d y}{d x}+4 y=0\)
Solution:
The auxiliary equations A.E is m² – 4m + 4 = 0
(m – 2)² = 0
m = 2, 2
Roots are real and equal
The complementary function (C.F) is (Ax + B) e^2x
The general solution is y = (Ax + B) e^2x

Question 3.
(D² + 2D + 3) y = 0
Solution:
The auxiliary equations A.E is m² + 2m + 3 = 0
⇒ m² + 2m + 1 + 2 = 0
⇒ (m + 1)² = -2
⇒ m + 1 = ± √2i
⇒ m = – 1 ± √2i
It is of the form α ± iβ
The complementary function (C.F) = e^-x [A cos √2 x + B sin √2 x]
The general solution is y = e^-x [A cos √2 x + B sin √2 x]

Question 4.
\(\frac{d^{2} y}{d x^{2}}-2 k \frac{d y}{d x}+k^{2} y=0\)
Solution:
Given (D² – 2kD + k²)y = 0, D = \(\frac{d}{d x}\)
The auxiliary equations is m² – 2km + k = 0
⇒ (m – k)² = 0
⇒ m = k, k
Roots are real and equal
The complementary function (C.F) is (Ax + B) e^kx
The general solution is y = (Ax + B) e^kx

Question 5.
(D² – 2D – 15) y = 0 given that \(\frac{d y}{d x}\) = 0 and \(\frac{d^{2} y}{d x^{2}}\) = 2 when x = 0
Solution:
A.E is m² – 2m – 15 = 0
(m – 5)(m + 3) = 0
m = 5, -3
C.F = Ae^5x + Be^-3x
The general solution is y = Ae^5x + Be^-3x …….. (1)

Question 6.
(4D² + 4D – 3) y = e^2x
Solution:
The auxiliary equations is 4m² + 4m – 3 = 0

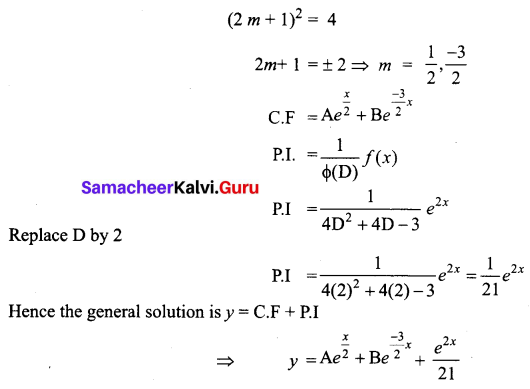
Question 7.
\(\frac{d^{2} y}{d x^{2}}\) + 16y = 0
Solution:
Given (D² + 16) y =0
The auxiliary equation is m² + 16 = 0
⇒ m² = -16
⇒ m = ± 4i
It is of the form α ± iβ, α = 0, β = 4
The complementary function (C.F) is e^0x [A cos 4x + B sin 4x]
The general solution is y = [A cos 4x + B sin 4x]

Question 8.
(D² – 3D + 2)y = e^3x which shall vanish for x = 0 and for x = log 2
Solution:
A.E is m² – 3m + 2 = 0
⇒ (m – 2) (m – 1) = 0
⇒ m = 2, 1
CF = Ae^2x + Be^x

Question 9.
(D² + D – 6)y = e^3x + e^-3x
Solution:
A.E is m² + m – 6 = 0
(m + 3) (m – 2) = 0

Question 10.
(D² – 10D + 25)y = 4e^5x + 5
Solution:
A.E is m² – 10m + 25 = 0
⇒ (m – 5)² = 0
⇒ m = 5, 5
C.F = (Ax + B) e^5x

Question 11.
(4D² + 16D + 15) y = 4\(e^{\frac{-3}{2} x}\)
Solution:
A.E is 4m² + 16m + 15 = 0
(2m + 3) (2m + 5) = 0

Question 12.
(3D² + D – 14)y = 13e^2x
Solution:

Question 13.
Suppose that the quantity demanded Q_d = 13 – 6p + 2\(\frac{d p}{d t}+\frac{d_{2} p}{d t^{2}}\) and quantity supplied Q_s = -3 + 2p where p is the price. Find the equilibrium price for market clearance.
Solution:
For market clearance, the required condition is Q_d = Q_s