Students can download 12th Business Maths Chapter 10 Operations Research Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Miscellaneous Problems
Question 1.
The following table summarizes the supply, demand and cost information for four factors S1, S2, S3, S4 shipping goods to three warehouses D1, D2, D3.
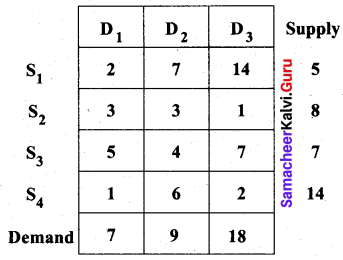
Find an initial solution by using the north-west corner rule. What is the total cost of this solution?
Solution:
Let ‘ai‘ denote the supply and ‘bj‘ denote the demand.
Then total supply = 5 + 8 + 7 + 14 = 34 and Total demand = 7 + 9 + 18 = 34
Σai = Σbj. So the problem is a balanced transportation problem and we can find a basic feasible solution, by North-west comer rule.
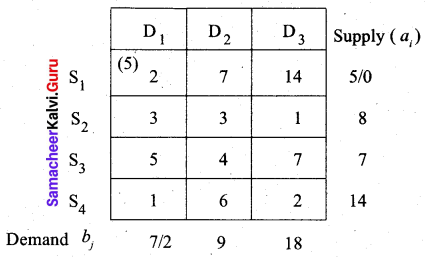
First allocation:
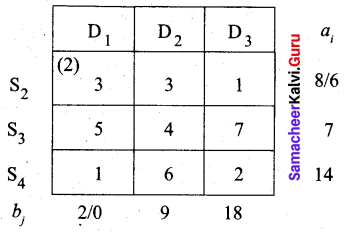
Second allocation:
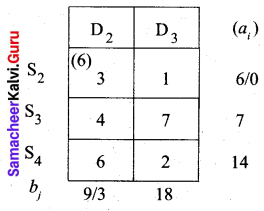
Third allocation:
Fourth allocation:
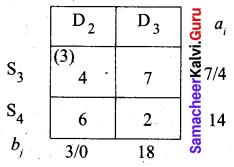
Fifth allocation:
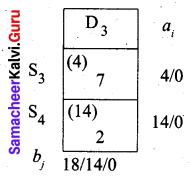
We first allot 4 units to cell (S3, D3) and then the balance 14 units to cell (S4, D3).
Thus we get the following allocations:
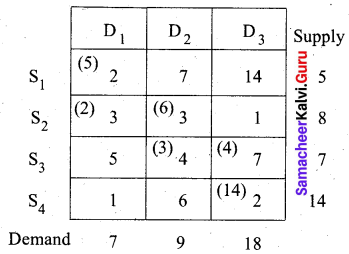
The transportation schedule:
S1 → D1, S2 → D1, S2 → D2, S3 → D2, S3 → D3, S4 → D3
(i.e) x11 = 5, x21 = 2, x22 = 6, x32 = 3, x33 = 4, x43 = 14
Total cost = (5 × 2) + (2 × 3) + (6 × 3) + (3 × 4) + (4 × 7) + (14 × 2)
= 10 + 6+ 18 + 12 + 28 + 28
= 102
Thus the initial basic solution is got by NWC method and minimum cost is Rs. 102.
Question 2.
Consider the following transportation problem
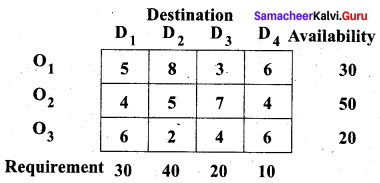
Determine an initial basic feasible solution using
(a) Least cost method
(b) Vogel’s approximation method
Solution:
Let ‘ai‘ denote the availability and ‘bj‘ denote the requirement. Then,
Σai = 30 + 50 + 20 = 100 and Σbj = 30 + 40 + 20 + 10 = 100
Since Σai = Σbj. the given problem is a balanced transportation problem and we can get an initial basic feasible solution.
(a) Least Cost Method (LCM)
First allocation:
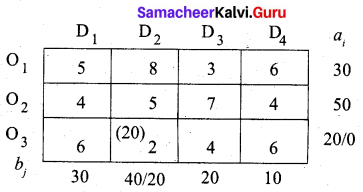
Second allocation:
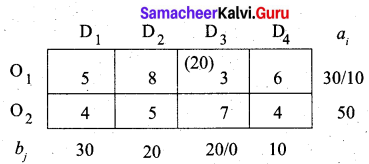
Third allocation:
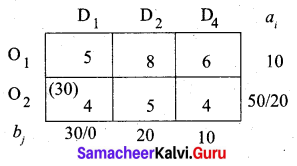
Fourth allocation:
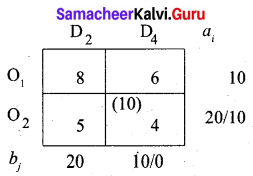
Fifth allocation:
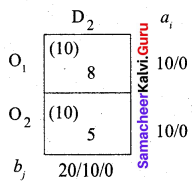
We first allocate 10 units to cell (O2, D2). Since it has a minimum cost. Then we allocate the balance 10 units to cell (O1, D2). Thus we get the final allocation table as given below.
Transportation schedule:
O1 → D2, O1 → D3, O2 → D1, O2 → D2, O2 → D4, O3 → D2
(i.e) x12 = 10, x13 = 20, x21 = 30, x22 = 10, x24 = 10, x32 = 20
The total cost is = (10 × 8) + (20 × 3) + (30 × 4) + (10 × 5) + (10 × 4) + (20 × 2)
= 80 + 60+ 120 + 50 + 40 + 40
= 390
Thus the LCM, we get the minimum cost for the transportation problem as Rs. 390.
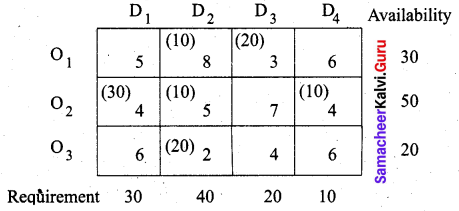
(b) Vogel’s approximation method:
First allocation:
The largest penalty = 3. So allocate 20 units to the cell (O3, D2) which has the least cost in column D2
Second allocation:

Largest penalty = 4. So allocate min (20, 30) units to the cell (O1, D3) which has the least cost in column D3
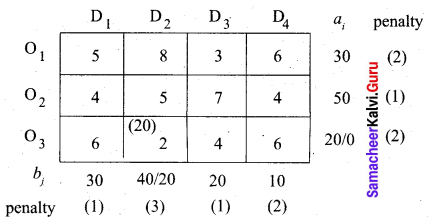
Third allocation:
The largest penalty is 3. So allocate min (20, 50) to the cell (O2, D2) which has the least cost in column D2.
Fourth allocation:
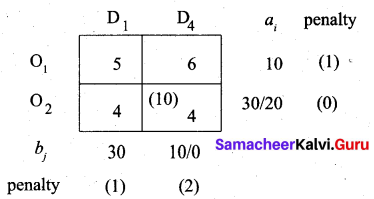
Largest penalty = 2. So allocate min (10, 30) to cell (O2, D4) which has the least cost in column D4
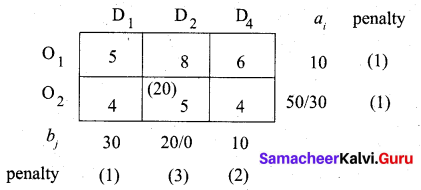
Fifth allocation:
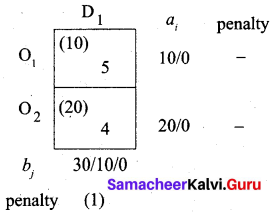
Largest penalty = 1. Allocate min (30, 20) to cell (O2, D1) which has the least cost in column D1. Finally allot the balance 10 units to cell (O1, D1)
We get the final allocation table as follows.
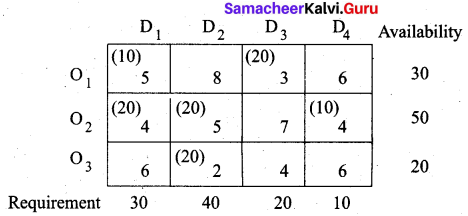
Transportation schedule:
O1 → D1, O1 → D3, O2 → D1, O2 → D2, O2 → D4, O3 → D2
(i.e) x11 = 10, x13 = 20, x21 = 20, x22 = 20, x24 = 10, x32 = 20
Total cost is given by = (10 × 5) + (20 × 3) + (20 × 4) + (20 × 5) + (10 × 4) + (20 × 2)
= 50 + 60 + 80+ 100 + 40 + 40
= 370
Hence the minimum cost by YAM is Rs. 370.
![]()
Question 3.
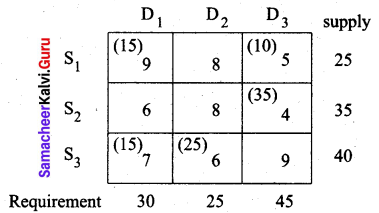
Determine an initial basic feasible solution to the following transportation problem by using (i) North-West Corner rule (ii) least-cost method.
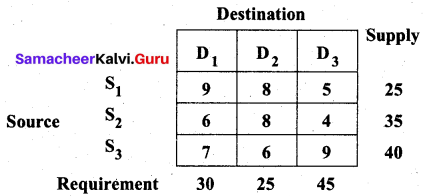
Solution:
Total supply = 25 + 35 + 40 = 100 = Σai
Total requirement = 30 + 25 + 45 = 100 = Σbj
Since Σai = Σbj the given transportation problem is balanced and we can find an initial basic feasible solution.
(i) North West Corner Rule
First allocation:
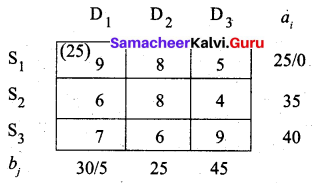
Second allocation:
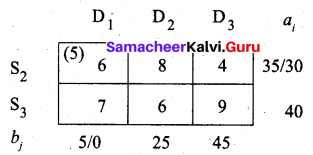
Third allocation:
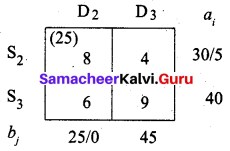
Fourth allocation:
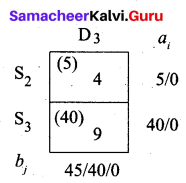
We first allot 5 units to cell (S2, D3). Then balance 40 units we allot to cell (S3, D3).
The final allotment is given as follows
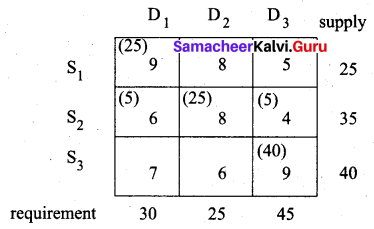
Transportation schedule:
S1 → D1, S2 → D1, S2 → D2, S2 → D3, S3 → D3
(i.e) x11 = 25, x21 = 5, x22 = 25, x23 = 5, x33 = 40
Total cost is = (25 × 9) + (5 × 6) + (25 × 8) + (5 × 4) + (40 × 9)
= 225 + 30 + 200 + 20 + 360
= 835
Hence the minimum cost is Rs. 835 by NWC method.
(ii) Least cost method (LCM)
First allocation:
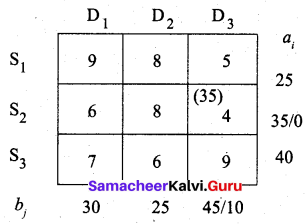
Second allocation:
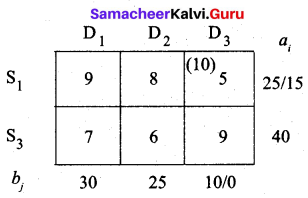
Third allocation:
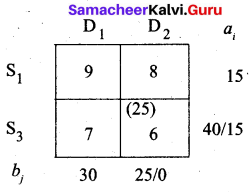
Fourth allocation:
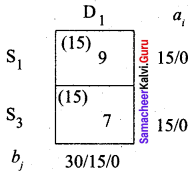
We first allot 15 units to cell (S3, D1) since it has the least cost. Then we allot the balance 15 units to cell (S1, D1).
The final allotment is given as follows
Transportation schedule:
S1 → D1, S1 → D3, S2 → D3, S3 → D1, S3 → D2
(i.e) x11 = 15, x13 = 10, x23 = 35, x31 = 15, x32 = 25
Total cost is = (15 × 9) + (10 × 5) + (35 × 4) + (15 × 7) + (25 × 6)
= 136 + 50 + 140 + 105 + 150
= 580
The optimal cost by LCM is Rs. 580.
Question 4.
Explain Vogel’s approximation method by obtaining an initial basic feasible solution to the following transportation problem.
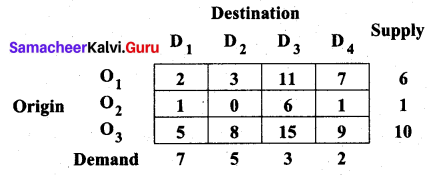
Solution:
Total supply (ai) = 6+1 + 10=17
Total demand (bj) = 7 + 5 + 3 + 2 = 17
Σai = Σbj. So given transportation problem is a balanced problem and hence we can find a basic feasible solution by VAM.
First allocation:
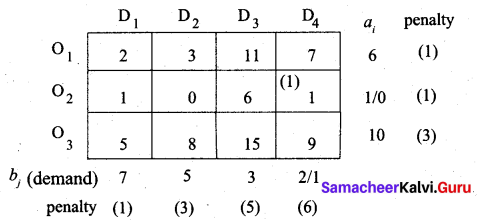
The largest penalty is 6. So allot min (2, 1) to the cell (O2, D4) which has the least cost in column D4.
Second allocation:
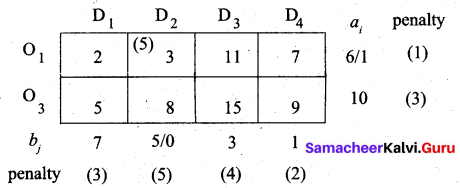
The largest penalty is 5. So allot min (5, 6) to the cell (O1, D2) which has the least cost in column D2.
Third allocation:
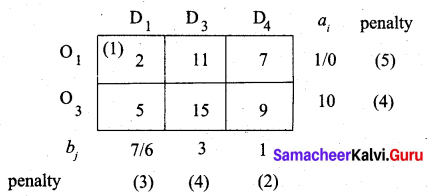
The largest penalty is 5. So allot min (7, 1) to the cell (O1, D1) which has the least cost in row O1.
Fourth allocation:
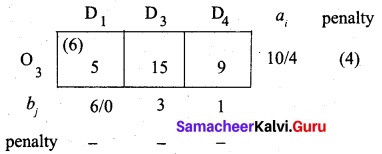
Largest penalty = 4. So allocate min (6, 10) to the cell (O3, D1) which has the least cost in row O3
Fifth allocation:
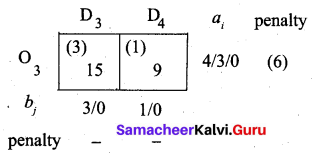
The largest penalty is 6. So allot min (1, 4) to the cell (O3, D4) which has the least cost in row O3. The balance 3 units is allotted to the cell (O3, D3). We get the final allocation as given below.
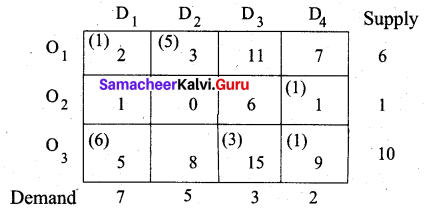
Transportation schedule:
O1 → D1, O1 → D2, O2 → D4, O3 → D1, O3 → D3, O3 → D4
(i.e) x11 = 1, x12 = 5, x24 = 1, x31 = 6, x33 = 3, x34 = 1
Total cost is given by = (1 × 2) + (5 × 3) + (1 × 1) + (6 × 5) + (3 × 15) + (1 × 9)
= 2 + 15 + 1 + 30 + 45 + 9
= 102
Thus the optimal (minimal) cost of the given transportation problem by Vogel’s approximation method is Rs. 102.
![]()
Question 5.
A car hire company has one car at each of five depots a, b, c, d and e. A customer in each of the fine towers A, B, C, D and E requires a car. The distance (in miles) between the depots (origins) and the towers (destinations) where the customers are given in the following distance matrix.
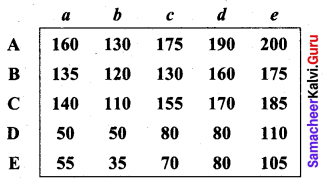
How should the cars be assigned to the customers so as to minimize the distance travelled?
Solution:
In the given assignment problem, the number of rows equals the number of columns. So the problem is balanced and we can get an optimal solution.
Step 1:
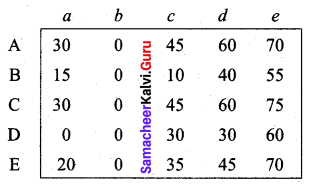
We have subtracted the minimum distance of each row from all elements of that row.
Step 2:
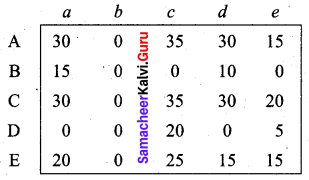
We have subtracted the minimum distance of each column from all elements of that column.
Step 3: (Assignment)
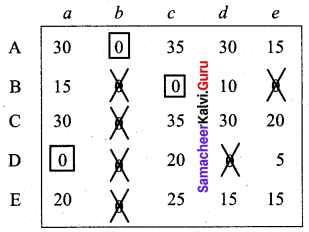
We are not able to assign depots for C and E. So we proceed as below.
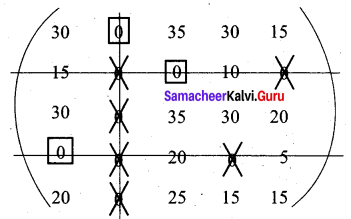
We have drawn a minimum number of lines to cover all zeros. Now 15 is the smallest element from all uncovered elements. Subtract this from all uncovered elements and add to the elements which lie at the intersection of two lines. Thus we obtain the following reduced matrix for fresh assignment.
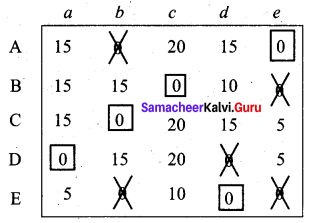
Assignment Schedule
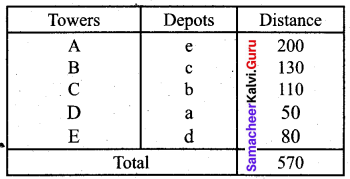
Thus the minimum distance is 570 miles.
Question 6.
A natural truck-rental service has a surplus of one truck in each of the cities 1, 2, 3, 4, 5 and 6 and a deficit of one truck in each of the cities 7, 8, 9, 10, 11 and 12. The distance (in kilometres) between the cities with a surplus and the cities with a deficit are displayed below:
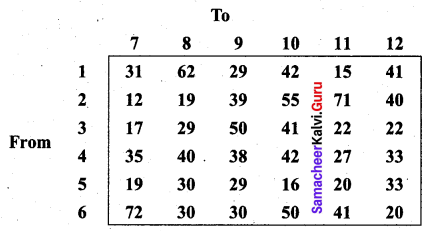
How should the truck be dispersed so as to minimize the total distance travelled?
Solution:
The number of rows equals the number of columns. So the problem is a balanced assignment problem and we can get an optimal solution.
Step 1: Subtract the minimum element of each row from all elements of that row.
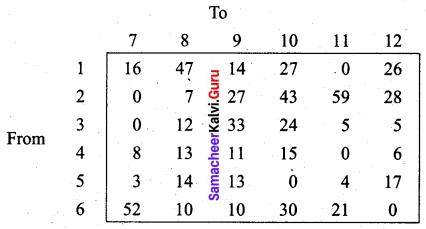
Step 2: Subtract the least element of each column from all elements of that column.
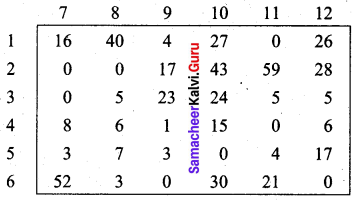
Step 3: (Assignment)
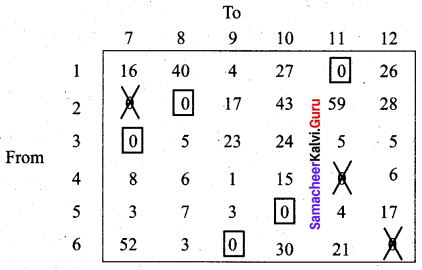
We are not able to assign city for starting place 4. We proceed as follows.
Draw a minimum number of lines to cover all the zeros of the matrix. Subtract the smallest element from all uncovered elements and add to the elements which lie at the intersection of two lines.
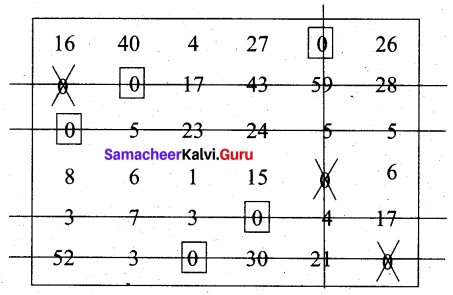
Then we obtain a new reduced matrix for fresh assignment.
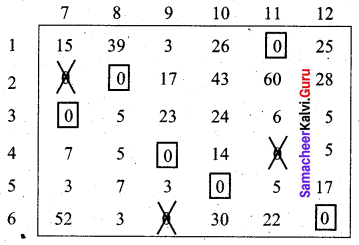
Final dispersal
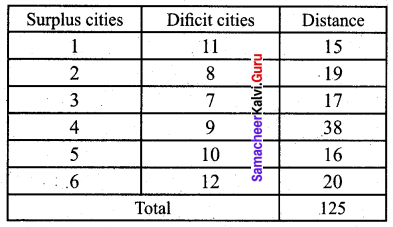
Thus the minimum total distance the trucks should travel is 125 km.
![]()
Question 7.
A person wants to invest in one of three alternative investment plans: Stock, Bonds and Debentures. It is assumed that the person wishes to invest all of the funds in a plan. The pay-off matrix based on three potential economic conditions is given in the following table:
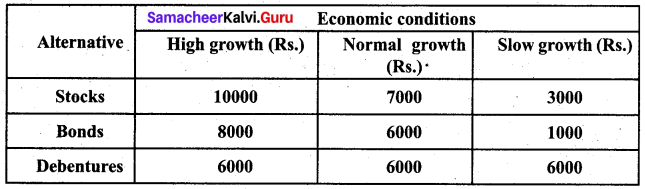
Determine the best investment plan using each of the following criteria (i) Maximin (ii) Minimax
Solution:
(i) Maximin rule
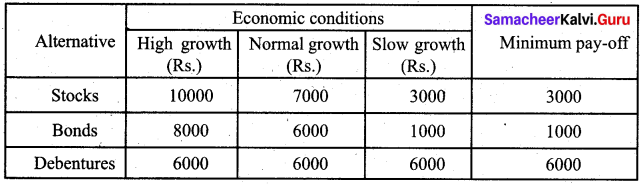
Max (3000, 1000, 6000) = 6000. Since the maximum value is 6000, he must invest in debentures by the maximin criteria.
(ii) Minimax rule
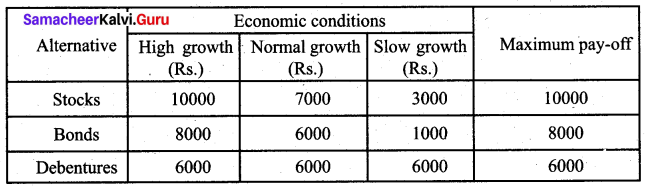
Min (10000, 8000, 6000) = 6000. Since the minimum value is 6000, he must invest in debentures by the minimax criteria.