Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.1

Students can download 12th Business Maths Chapter 10 Operations Research Ex 10.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.1

Question 1.
What is the transportation problem?
Solution:
The transportation problem deals with transporting goods from a source to a destination by minimum cost.
Description: A Manufacturer has a number of factories which produces goods at a fixed rate. He also has a number of warehouses, each of which has a fixed storage capacity. There is a cost to transport goods from a factory to a warehouse. Find the transportation of goods from factory to the warehouse that has the lowest possible cost.
Example:
Factories:
A₁ makes 5 units
A₂ makes 4 units
A₃ makes 6 units
Warehouses:
b₁ can store 5 units
b₂ can store 3 units
b₃ can store 5 units
b₄ can store 2 units
Transportation costs:

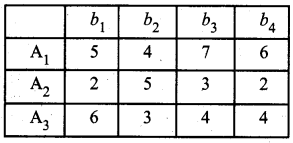
Question 2.
Write the mathematical form of transportation problem.
Solution:
Mathematically a transportation problem is nothing but a special linear programming problem in which the objective function is to minimize the cost of transportation subjected to the demand and supply constraints.
Let there be ‘m’ sources of supply having ‘a_i‘ units of supplies respectively to be transported among ‘n’ destinations with ‘b_j‘ units of requirements respectively. Let C_ij be the cost of shipping one unit of the commodity from source i to destination j for each route. Let x_ij be the units shipped per route.
Then the LPP is stated below.

Question 3.
What are a feasible solution and non-degenerate solution in the transportation problem?
Solution:
Feasible Solution: A feasible solution to a transportation problem is a set of non-negative values x_ij (i = 1, 2,.., m, j = 1, 2, …n) that satisfies the constraints.
Non-degenerate basic feasible Solution: If a basic feasible solution to a transportation problem contains exactly m + n – 1 allocation in independent positions, it is called a Non-degenerate basic feasible solution. Here m is the number of rows and n is the number of columns in a transportation problem.

Question 4.
What do you mean by balanced transportation problem?
Solution:
The balanced transportation problem is a transportation problem where the total availability at the origins is equal to the total requirements at the destinations.

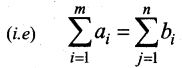
A feasible solution can be obtained to these problems by Northwest comer method, minimum cost method (or) Vogel’s approximation method.

Question 5.
Find an initial basic feasible solution of the following problem using north-west corner rule.

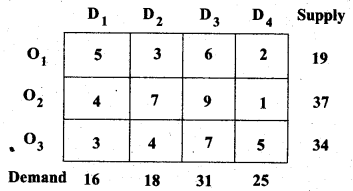
Solution:
Given the transportation table is

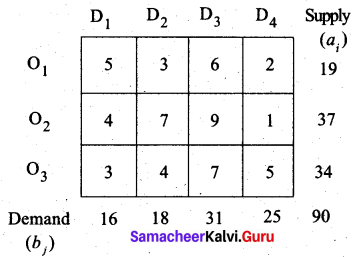
Total supply = Total Demand = 90.
The given problem is a balanced transportation problem.
Hence there exists a feasible solution to the given problem.
First allocation:

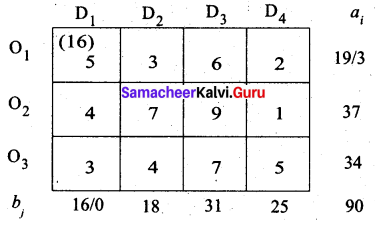
Second allocation:

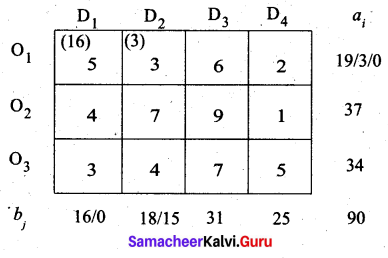
Third allocation:

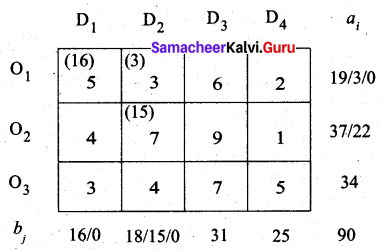
Fourth allocation:

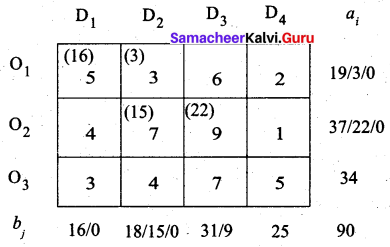
Fifth allocation:

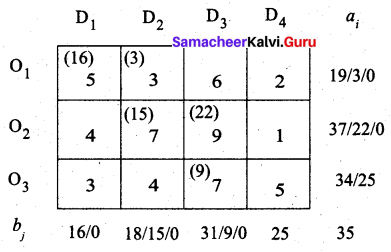
Final allocation:

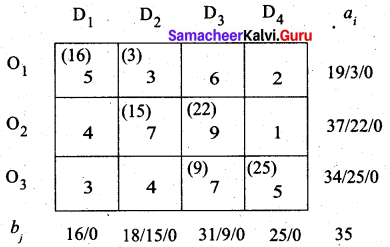
Transportation schedule:
O₁ → D₁, O₁ → D₂, O₂ → D₂, O₂ → D₃, O₃ → D₃, O₃ → D₄
(i.e) x₁₁ = 16, x₁₂ = 3, x₂₂ = 15, x₂₃ = 22, x₃₃ = 9, x₃₄ = 25.
Total transportation cost = (16 × 5) + (3 × 3) + (15 × 7) + (22 × 9) + (9 × 7) + (25 × 5)
= 80 + 9 + 105 + 198 + 63 + 125
= 580
Thus the minimum cost is Rs. 580 using the north west comer rule.

Question 6.
Determine an initial basic feasible solution of the following transportation problem by north-west corner method.

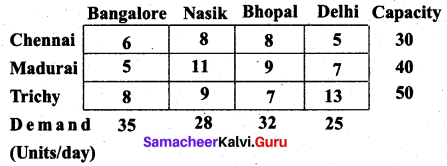
Solution:
Let B, N, Bh, D represent the destinations Bangalore, Nasik, Bhopal and Delhi respectively.
Let C, M, T represent the starting places Chennai, Madurai and Trichy respectively.
The given transportation table is

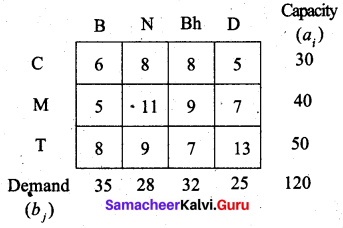
Total capacity = Total Demand = 120.
So the given problem is a balanced transportation problem.
Hence there exists a feasible solution to the given problem.
First allocation:

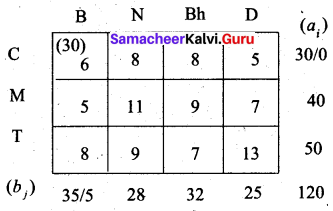
Second allocation:

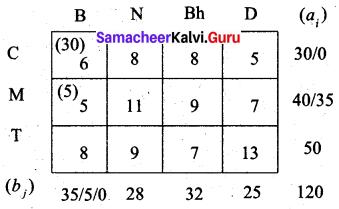
Third allocation:

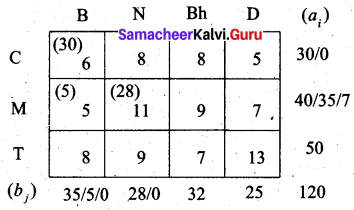
Fourth allocation:

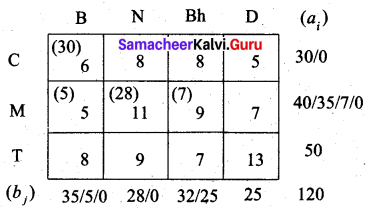
Fifth allocation:

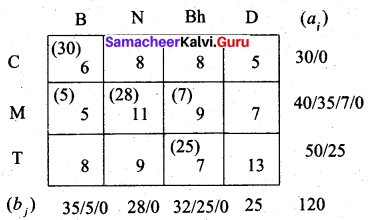
Final allocation:

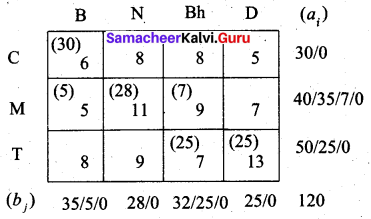
Transportation schedule:
Chennai to Bangalore, Madurai to Bangalore, Madurai to Nasik, Madurai to Bhopal, Trichy to Bhopal, Trichy to Delhi.
(i.e) x₁₁ = 30, x₂₁ = 5, x₂₂ = 28, x₂₃ = 7, x₃₃ = 25, x₃₄ = 25
The total transportation cost = (30 × 6) + (5 × 5) + (28 × 11) + (7 × 9) + (25 × 7) + (25 × 13)
= 180 + 25 + 308 + 63 + 175 + 325
= 1076
Thus the minimum cost is Rs. 1076 by the north west comer method.

Question 7.
Obtain an initial basic feasible solution to the following transportation problem by using the least-cost method.

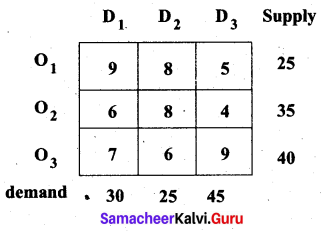
Solution:
Total supply = 25 + 35 + 40 = 100
Total demand = 30 + 25 + 45 = 100
Total supply = Total demand
∴ The given problem is a balanced transportation problem. Hence there exists a feasible solution to the given problem. Let ‘ai’ denote the supply and ‘bj’ denote the demand. We allocate the units according to the least transportation cost of each cell.
First allocation:

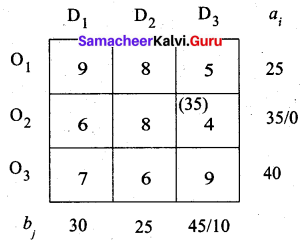
The least-cost 4 corresponds to cell (O₂, D₃). So first we allocate to this cell.
Second allocation:

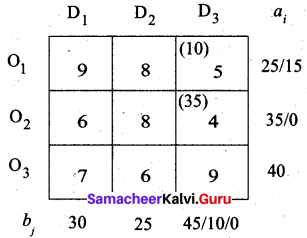
The least-cost 5 corresponds to cell (O₁, D₃). So we have allocated min (10, 25) to this cell.
Third allocation:

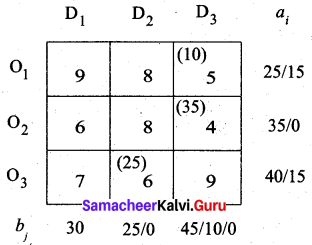
The least-cost 6 corresponds to cell (O₃, D₂). So we have allocated min (25, 40) to this cell.
Fourth allocation:

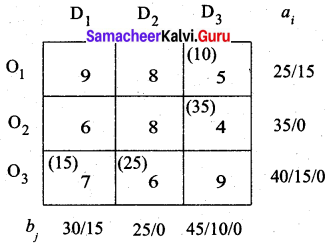
The least-cost 7 corresponds to cell (O₃, D₁). So we have allocated min (30, 15) to this cell.
Final allocation:
Although the next least cost is 8, we cannot allocate to cells (O₁, D₂) and (O₂, D₂) because we have exhausted the demand 25 for this column. So we allocate 15 to cell (O₁, D₁)

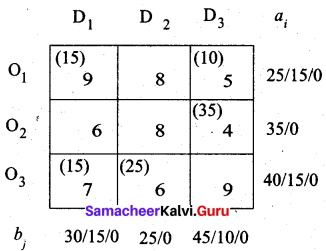
Transportation schedule: O₁ → D₁, O₁ → D₃, O₂ → D₃, O₃ → D₁, O₃ → D₂
(i.e) x₁₁ = 15, x₁₃ = 10, x₂₃ = 35, x₃₁ = 15, x₃₂ = 25
Total cost is = (15 × 9) + (10 × 5) + (35 × 4) + (15 × 7) + (25 × 6)
= 135 + 50 + 140 + 105 + 150
= 580
Thus by least cost method (LCM) the cost is Rs. 580.

Question 8.
Explain Vogel’s approximation method by obtaining an initial feasible solution of the following transportation problem

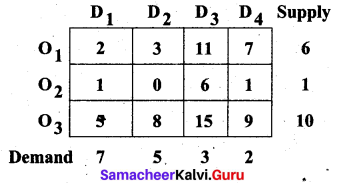
Solution:
Let ‘a_i‘ denote the supply and ‘b_j‘ denote the demand Σa_i = 6 + 1 + 10 = 17 and Σb_j = 7 + 5 + 3 + 2 = 17
Σa_i = Σb_j (i.e) Total supply = Total demand. the given problem is a balanced transportation problem. Hence there exists a feasible solution to the given problem.
First, we find the difference (penalty) between the first two smallest costs in each row and column and write them in brackets against the respective rows and columns.
First allocation:

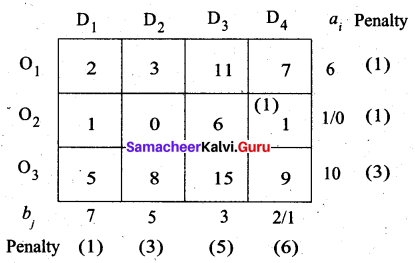
The largest difference is 6 corresponding to column D₄. In this column least cost is (O₂, D₄). Allocate min (2, 1) to this cell.
Second allocation:

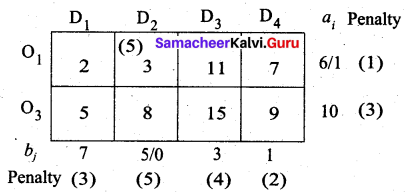
The largest difference is 5 in column D₂. Here the least cost is (O₁, D₂). So allocate min (5, 6) to this cell.
Third allocation:

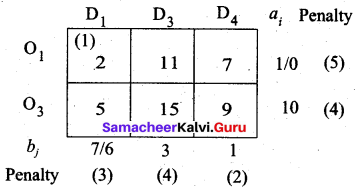
The largest penalty is 5 in row O₁. The least cost is in (O₁, D₁). So allocate min (7, 1) here.
Fourth allocation:

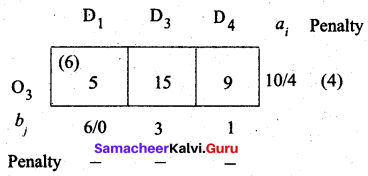
Fifth allocation:

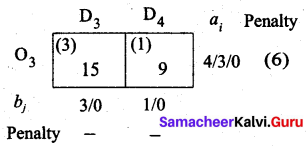
We allocate min (1, 4) to (O₃, D₄) cell since it has the least cost. Finally the balance we allot to cell (O₃, D₃).
Thus we have the following allocations:

Transportation schedule:
O₁ → D₁, O₁ → D₂, O₂ → D₄, O₃ → D₁, O₃ → D₃, O₃ → D₄
(i.e) x₁₁ = 12, x₁₂ = 5, x₂₄ = 1, x₃₁ = 6, x₃₃ = 3, x₃₄ = 1
Total cost = (1 × 2) + (5 × 3) + (1 × 1) + (6 × 5) + (3 × 15) + (1 × 9)
= 2 + 15 + 1 + 30 + 45 + 9
= 102

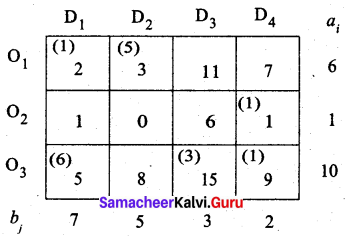
Question 9.
Consider the following transportation problem.

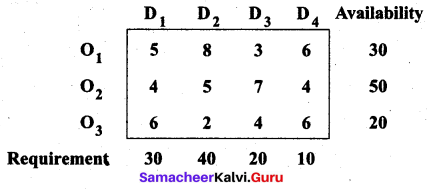
Determine initial basic feasible solution by VAM
Solution:
Let ‘a_i‘ denote the availability and ’b_j‘ denote the requirement
Σai = 30 + 50 + 20 = 100 and Σbj = 30 + 40 + 20 + 10 = 100
Σa_i = Σb_j So the given problem is a balanced transportation problem. Hence there exists a feasible solution to the given problem.
For VAM, we first find the penalties for rows and columns. We allocate units to the maximum penalty column (or) row with the least cost.
First allocation:

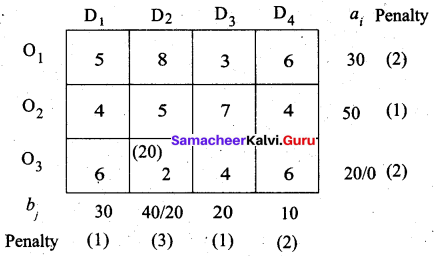
Largest penalty = 3. allocate min (40, 20) to (O₃, D₂)
Second allocation:

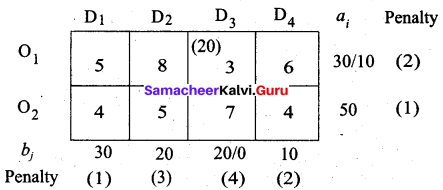
Largest penalty = 4. Allocate min (20, 30) to (O₁, D₃)
Third allocation:

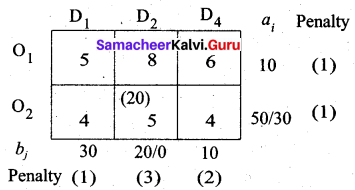
The largest penalty is 3. Allocate min (20, 50) to (O₂, D₂)
Fourth allocation:

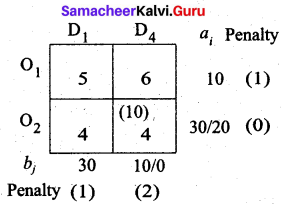
The largest penalty is 2, Allocate min (10, 30) to (O₂, D₄)
Fifth allocation:

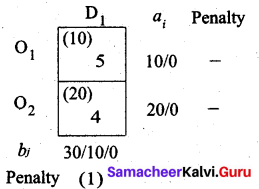
The largest penalty is 1. Allocate min (30, 20) to (O₂, D₁)
Balance 10 units we allot to (O₁, D₁).
Thus we have the following allocations:

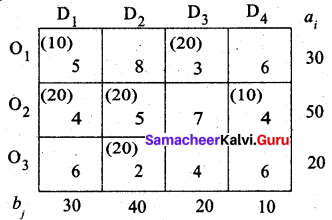
Transportation schedule:
O₁ → D₁, O₁ → D₃, O₂ → D₁, O₂ → D₂, O₂ → D₄, O₃ → P₂
(i.e) x₁₁ = 10, x₁₃ = 20, x₂₁ = 20, x₂₂ = 20, x₂₄ = 10, x₃₂ = 20
Total cost = (10 × 5) + (20 × 3) + (20 × 4) + (20 × 5) + (10 × 4) + (20 × 2)
= 50 + 60 + 80 + 100 + 40 + 40
= 370
Thus the least cost by YAM is Rs. 370.

Question 10.
Determine the basic feasible solution to the following transportation problem using North West Corner rule.

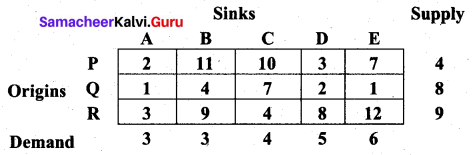
Solution:
For the given problem, total supply is 4 + 8 + 9 = 21 and total demand is 3 + 3 + 4 + 5 + 6 = 21.
Since the total supply equals total demand, it is a balanced problem and we can find a feasible solution by North West Comer rule.
First allocation:

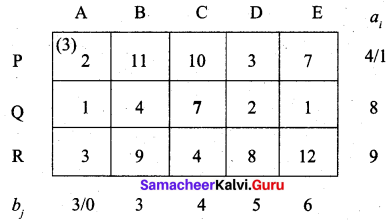
Second allocation:

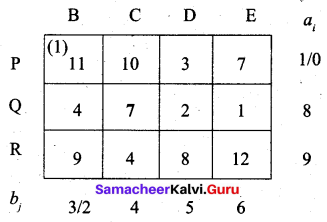
Third allocation:

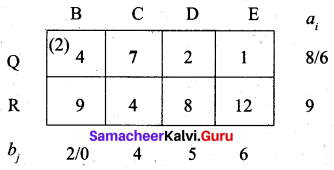
Fourth allocation:

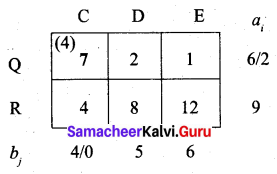
Fifth allocation:

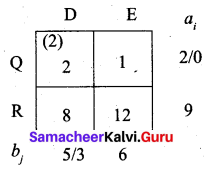
Final allocation:

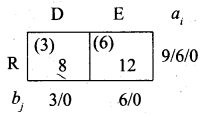
First, we allow 3 units to (R, D) cell. Then balance 6 to (R, E) cell.
Thus we have the following allocations:

Transportation schedule:
P → A, P → B, Q → B, Q → C, Q → D, R → D, R → E
(i.e) x₁₁ = 3, x₁₂ = 1, x₂₂ = 2, x₂₃ = 4, x₂₄ = 2, x₃₄ = 3, x₃₅ = 6
Total cost = (3 × 2) + (1 × 11) + (2 × 4) + (4 × 7) + (2 × 2) + (3 × 8) + (6 × 12)
= 6 + 11 + 8 + 28 + 4 + 24 + 72
= 153
Thus the minimum cost of the transportation problem by Northwest Comer rule is Rs. 153.

Question 11.
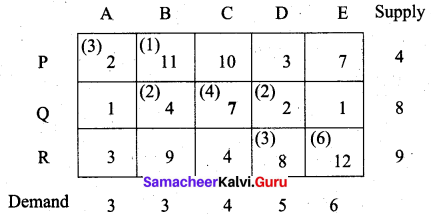
Find the initial basic feasible solution of the following transportation problem:

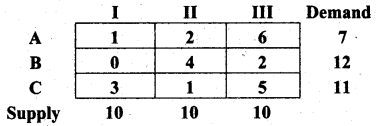
Using (i) North West Corner rule
(ii) Least Cost method
(iii) Vogel’s approximation method
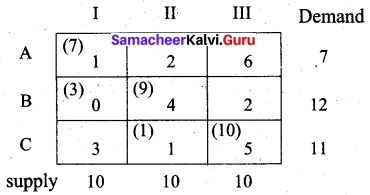
Solution:
Total demand (a_i) = 7 + 12 + 11 = 30 and total supply (b_j) = 10 + 10 + 10 = 30.
Σa_i = Σb_j ⇒ the problem is a balanced transportation problem and we can find a basic feasible solution.
(i) North West Comer rule (NWC)
First allocation:

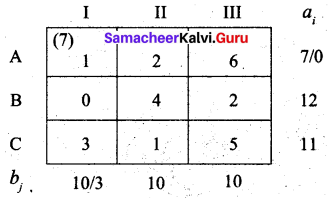
Second allocation:

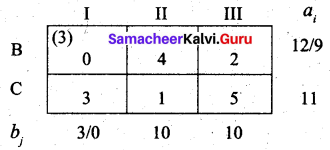
Third allocation:

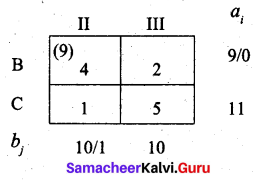
Fourth allocation:

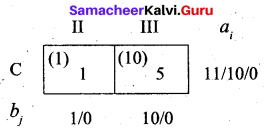
We first allot 1 unit to (C, II) cell and then the balance 10 units to (C, III) cell.
Thus we have the following allocations:

Transportation schedule:
A → I, B → I, B → II, C → II, C → III
(i.e) x₁₁ = 7, x₂₁ = 3, x₂₂ = 9, x₃₂ = 1, x₃₃ = 10
Total cost = (7 × 1) + (3 × 0) + (9 × 4) + (1 × 1) + (10 × 5)
= 7 + 0 + 36 + 1 + 50
= Rs. 94

(ii) Least Cost method
First allocation:

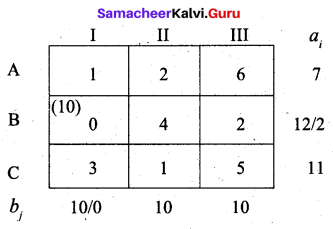
Second allocation:

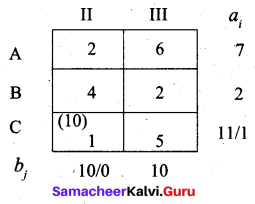
Third allocation:

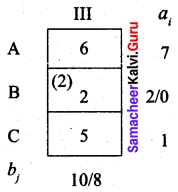
Fourth allocation:

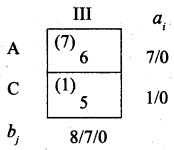
We first allot 1 unit to cell (C, III) and the balance 7 units to cell (A, III).
Thus we have the following allocations:

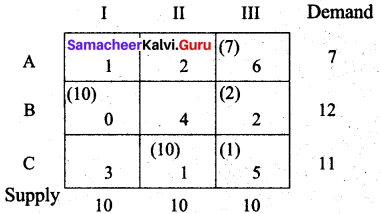
Transportation schedule:
A → III, B → I, B → III, C → II, C → III
(i.e) x₁₃ = 7, x₂₁ = 10, x₂₃ = 2, x₃₂ = 10, x₃₃ = 1
Total cost = (7 × 6) + (10 × 0) + (2 × 2) + (10 × 1) + (1 × 5)
= 42 + 0 + 4 + 10 + 5
= Rs. 61

(iii) Vogel’s approximation method (VAM)
First allocation:

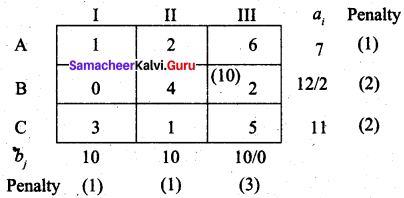
Largest penalty = 3. Allocate min (10, 12) to (B, III)
Second allocation:

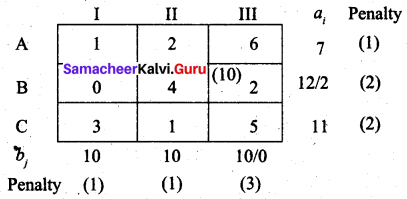
Largest penalty = 4. Allocate min (10, 2) to cell (B, I)
Third allocation:

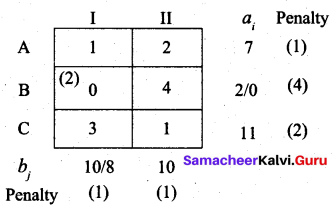
The largest penalty is 2. We can choose I column or C row. Allocate min (8, 7) to cell (A, I)
Fourth allocation:

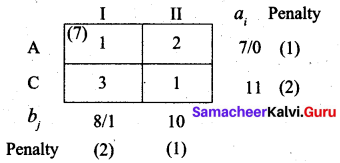
First, we allocate 10 units to cell (C, II). Then balance 1 unit we allot to cell (C, I)
Thus we have the following allocations:

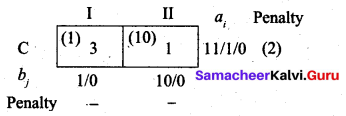
TYansportation schedule:
A → I, B → I, B → III, C → I, C → II
(i.e) x₁₁ = 7, x₂₁ = 2, x₂₃ = 10, x₃₁ = 1, x₃₂ = 10
Total cost = (7 × 1) + (2 × 0) + (10 × 2) + (1 × 3) + (10 × 1)
= 7 + 0 + 20 + 3 + 10
= Rs. 40

Question 12.
Obtain an initial basic feasible solution to the following transportation problem by north-west corner method.

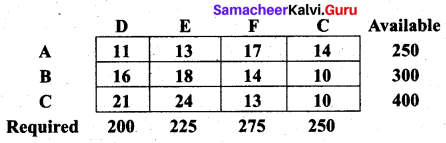
Solution:
Total availability is 250 + 300 + 400 = 950
Total requirement is 200 + 225 + 275 + 250 = 950
Since Σa_i = Σb_j the problem is a balanced transportation problem and we can find an initial basic feasible solution.
First Allocation:

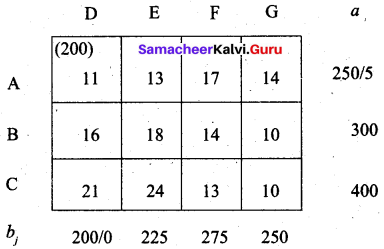
Second allocation:

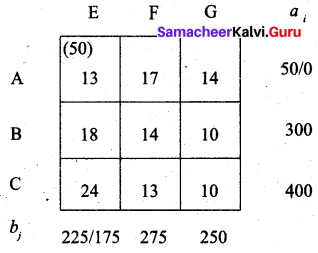
Third allocation:

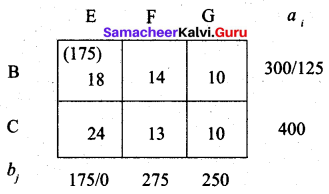
Fourth allocation:

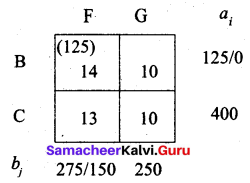
Fifth allocation:

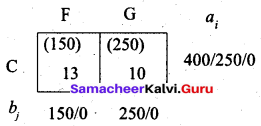
We first allocate 150 units to cell (C, F). Then we allocate balance of 250 units to cell (C, G)
Thus we have the following allocation.

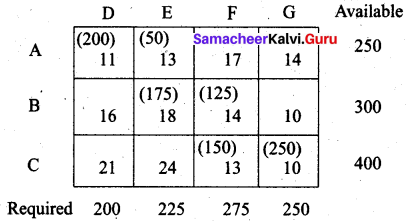
Transportation schedule:
A → D, A → E, B → E, B → F, C → F, C → G
(i.e) x₁₁ = 200, x₁₂ = 50, x₂₂ = 175, x₂₃ = 125, x₃₃ = 150, x₃₄ = 250
Total cost = (200 × 11) + (50 × 13) + (175 × 18) + (125 × 14) + (150 × 13) + (250 × 10)
= 2200 + 650 + 3150 + 1750 + 1950 + 2500
= Rs. 12,200