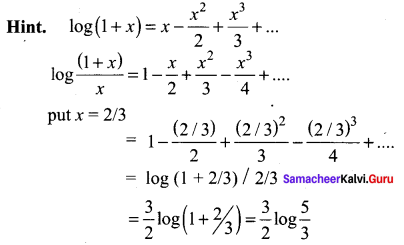You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.5
Choose the correct or the most suitable answer:
Question 1.
The value of 2 + 4 + 6 + … + 2n is …..
Solution:
(d) n(n + 1)
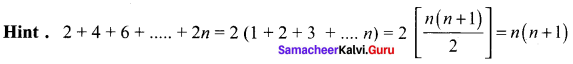
Question 2.
The coefficient of x6 in (2 + 2x)10 is ……….
(a) 10C6
(b) 26
(c) 10C626
(d) 10C6210
Solution:
(d) 10C6210
Hint.
tr + 1 = 210(nCr)
To find coefficient of x6 put r = 6
∴ coefficient of x6 = 210 [10C6]
Question 3.
The coefficient of x8y12 in the expansion of (2x + 3y)20 is …….
(a) 0
(b) 28312
(c) 28312 + 21238
(d) 20C828312
Solution:
(d) 20C828312
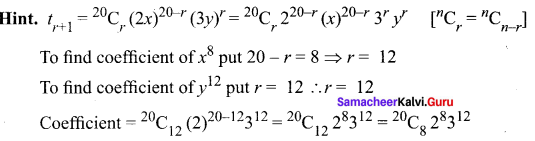
![]()
Question 4.
If nC10 > nCr for all possible r, then a value of n is ……..
(a) 10
(b) 21
(c) 19
(d) 20
Solution:
(d) 20
Hint.
Out of 10C10, 21C10, 19C10 and 20C10, 20C10 is larger.
Question 5.
If a is the arithmetic mean and g is the geometric mean of two numbers, then ……..
(a) a ≤ g
(b) a ≥ g
(c) a = g
(d) a > g
Solution:
(b) a ≥ g
Hint. AM ≥ GM
∴ a ≥ g
Question 6.
If (1 + x2)2 (1 + x)n = a0 + a1x + a2x2 + …. + xn + 4 and if a0, a1, a2 are in AP, then n is ……
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b or c)n = 2 or 3
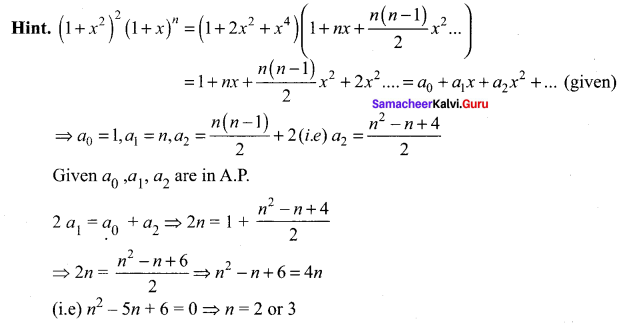
Question 7.
If a, 8, b are in A.P, a, 4, b are in G.P, if a, x, b are in HP then x is ……
(a) 2
(b) 1
(c) 4
(d) 16
Solution:
(a) 2

Question 8.
(a) AP
(b) GP
(c) HP
(d) AGP
Solution:
(c) HP
![]()
Question 9.
The HM of two positive numbers whose AM and GM are 16, 8 respectively is ………
(a) 10
(b) 6
(c) 5
(d) 4
Solution:
(d) 4
Hint.
Let the two numbers be a and b
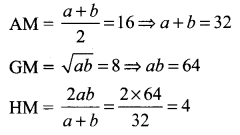
Question 10.
If Sn denotes the sum of n terms of an AP whose common difference is d, the value of \(\mathrm{S}_{n}-2 \mathrm{S}_{n-1}+S_{n-2}\) is ……
(a) d
(b) 2d
(c) 4d
(d) d2
Solution:
(a) d
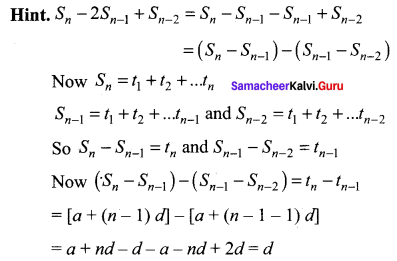
![]()
Question 11.
The remainder when 3815 is divided by 13 is …….
(a) 12
(b) 1
(c) 11
(d) 5
Solution:
(a) 12
Hint.
3815 = (39 – 1)15 = 3915 – 15C1 3914(1) + 15C2 (39)13(1)2 – 15C3 (39)12(1)3 ….. + 15C14 (39)1(1) – 15C15(1)
Except -1 all other terms are divisible by 13.
∴ When 1 is added to it the number is divisible by 13. So the remainder is 13 – 1 = 12.
Question 12.
The nth term of the sequence 1, 2, 4, 7, 11, …… is

Solution:
(d) \(\frac{n^{2}-n+2}{2}\)
Question 13.
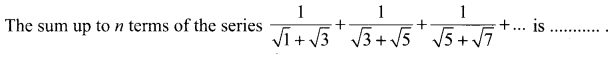
Solution:

Solution:
(d) \(\frac{\sqrt{2 n+1}-1}{2}\)
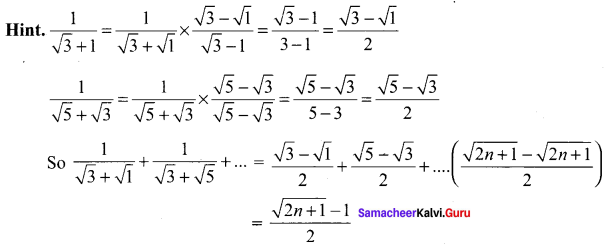
Question 14.
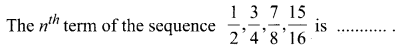
![]()
Solution:
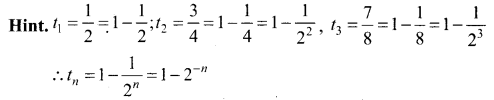
![]()
Question 15.
![]()
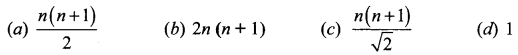
Solution:
(c) \(\frac{n(n+1)}{\sqrt{2}}\)

Question 16.
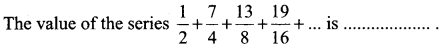
(a) 14
(b) 7
(c) 4
(d) 6
Solution:
(a) 14
Question 17.
The sum of an infinite GP is 18. If the first term is 6, the common ratio is ………
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{3}{4}\)
Solution:
(b) \(\frac{2}{3}\)
Hint:
![]()
18r = 18 – 6 = 12
r = 12/18 = 2/3
Question 18.
The coefficient of x5 in the series e-2x is ………
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{-4}{15}\)
(d) \(\frac{4}{15}\)
Answer:
(c) \(\frac{-4}{15}\)
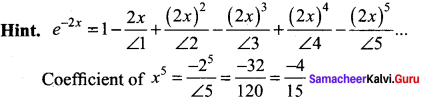
![]()
Question 19.
![]()
Answer:
(c) \(\frac{(e-1)^{2}}{2 e}\)

Question 20.
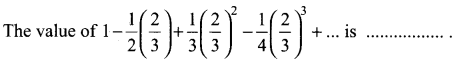
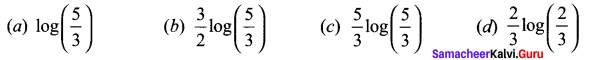
Solution:
(b) \(\frac{3}{2} \log \left(\frac{5}{3}\right)\)