You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.3
11th Maths Exercise 2.3 Question 1.
Represent the following inequalities in the interval notation:
Solution:
![]()
⇒ x ∈ [-1, 4)
[] closed interval, end points are included
() ➝ open interval
end points are excluded
(ii) x ≤ 5 and x ≥ -3[i] x ≤ 5 and x ≥ -3
Solution:

x ∈ [-3, 5)
(iii) x < -1 or x < 3
Solution:
![]()
x ∈ (-∞, -1) or x ∈ (-∞, 3)
(iv) – 2x > 0 or 3x – 4 < 11
Solution:
-2x > 0 ⇒ 2x < 0 ⇒ x < 0
x ∈ (-∞, 0)
3x – 4 < 11
⇒ 3x – 4 + 4 < 11 + 4
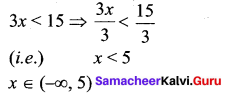
11th Maths Exercise 2.3 Answers Question 2.
Solve 23x < 100 when
(i) x is a natural number,
(ii) x is an integer.
Solution:
23x <100
![]()
(i.e.,) x > 4.3
(i) x = 1, 2, 3, 4 (x ∈ N)
(ii) x = …. -3, -2, -1, 0, 1, 2, 3, 4 (x ∈ Z)
11th Maths Chapter 2 Solution Samacheer Kalvi Question 3.
Solve -2x ≥ 9 when
(i) x is a real number,
(ii) x is an integer,
(iii) x is a natural number.
Solution:
-2x > 9 ⇒ 2x ≤ -9

(ii) x = …. -3, -2, -1, 0, 1, 2, 3, 4
(iii) x = 1, 2, 3, 4
Samacheer Kalvi 11th Maths Solution Question 4.
![]()
Solution:

(ii)
![]()
Solution:
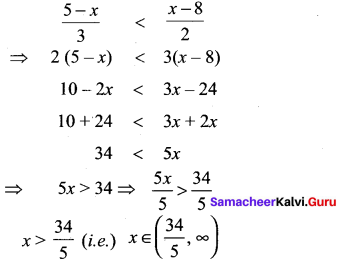
Samacheer Kalvi 11th Maths Example Sums Question 5.
To secure A grade one must obtain an average of 90 marks or more in 5 subjects each of maximum 100 marks. If one scored 84, 87, 95, 91 in first four subjects, what is the minimum mark one scored in the fifth subject to get A grade in the course?
Solution:
Required marks = 5 × 90 = 450
Total marks obtained in 4 subjects = 84 + 87+95 + 91 = 357
So required marks in the fifth subject = 450 – 357 = 93
Samacheer Kalvi 11th Maths Solutions Question 6.
A manufacturer has 600 litres of a 12 percent solution of acid. How many litres of a 30 percent acid solution must be added to it so that the acid content in the resulting mixture will be more than 15 percent but less than 18 percent?
Solution:
12% solution of acid in 600 l ⇒ 600 × \(\frac{12}{100}\) = 72 l of acid
15% of 600 l ⇒ 600 × \(\frac{15}{100}\) = 90 l
18% of 600 l ⇒ 600 × \(\frac{18}{100}\) = 108 l
Let x litres of 18% acid solution be added
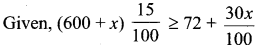
(600 + x)15 ≥ 7200 + 30x
9000+ 15x ≥ 7200 + 30x
1800 ≥ 15x
x ≤ 120
Let x litres of 18% acid solution be added
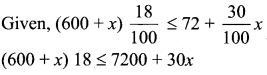
10800 + 18 ≤ 7200 + 30x
3600 ≤ 12x
x > 300
The solution is 120 ≤ x > 300
Samacheer Kalvi Class 11 Maths Solutions Question 7.
Find all pairs of consecutive odd natural numbers both of which are larger than 10 and their sum is less than 40.
Solution:
Let the two numbers be x and x + 2
x + x + 2 < 40
⇒ 2x < 38

⇒ x< 19 and x > 10
so x = 11 ⇒ x + 2 = 13
x = 13 ⇒ x + 2 = 15
x = 15 ⇒ x + 2 = 17
When x = 17 ⇒ x + 2 = 19
So the possible pairs are (11, 13), (13, 15), (15, 17), (17, 19)
Samacheer Kalvi 11 Maths Solutions Question 8.
A model rocket is launched from the ground. The height h of the rocket after t seconds from lift off is given by h(t) = -5t2 + 100t; 0 ≤ r ≤ 20. At what time the rocket is 495 feet above the ground?
Solution:
h(t) = -5t2 + 1oot
at t = 0, h(0) = 0
at t = 1, h(1) = -5 + 100 = 95
at t = 2, h(2) = -20 + 200 = 180
at t =3, h(3) = -45 + 300 = 255
at t = 4, h(4) = -80 + 400 = 320
at t = 5, h(5) = -125 + 500 = 375
at t = 6, h(6) = – 180 + 600 = 420
at t = 7, h(7) = -245 + 700 = 455
at t = 8, h(8) = – 320 + 800 = 480
at t = 9, h(9) = -405 + 900 = 495
So, at 9 secs, the rocket is 495 feet above the ground.
Samacheer Kalvi 11th Maths Answers Question 9.
A Plumber can be paid according to the following schemes: In the first scheme he will be paid Rs. 500 plus Rs.70 per hour, and in the second scheme he will be paid Rs. 120 per hour. If he works x hours, then for what value of x does the first scheme give better wages?
Solution:
I scheme with x hr
500 + (x- 1) 70 = 500 + 70x – 70
= 430 + 70x
II scheme with x hours
120x
Here I > II
⇒ 430 + 70x > 120x
⇒ 120x – 70x < 430
50x < 430
\(\frac{50 x}{50}<\frac{430}{50}\)
x < 8.6 (i.e.) when x is less than 9 hrs the first scheme gives better wages.
Samacheer Kalvi Guru 11th Maths Question 10.
A and B are working on similar jobs but their annual salaries differ by more than Rs 6000. If B earns Rs. 27000 per month, then what are the possibilities of A’s salary per month?
Solution:
A’s monthly salary = ₹ x
B’s monthly salary = ₹ 27000
Their annual salaries differ by ₹ 6000
A’s salary – 27000 > 6000
A’s salary > ₹ 33000
B’s salary – A’s salary > 6000
27000 – A’s salary > 6000
A’s salary < ₹ 21000
A’s monthly salary will be lesser than ₹ 21,000 or greater than ₹ 33,000
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.3 Additional Questions
11th Maths Solutions Samacheer Kalvi Question 1.
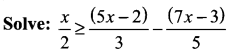
Solution:

Multiplying both sides by 30, we get 15x ≥ 2(4x – 1) ⇒ 15x ≥ 8x – 2⇒ 15x – 8x ≥ -2
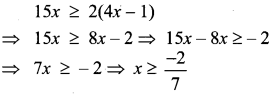
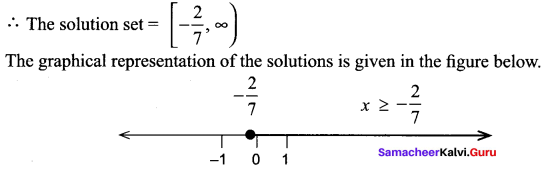
11th Maths Samacheer Kalvi Solutions Question 2.
Ravi obtained 70 and 75 marks in first two unit tests. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
Solution:
Let x be the marks obtained by Ravi in the third test.
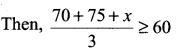
⇒ 145 + x ≥ 180 ⇒ x >180 – 145
⇒ x ≥ 35
Thus, Ravi must obtain a minimum of 35 marks to get an average of at least 60 marks.
Note. A minimum of 35 marks.
⇒ Marks greater than or equal to 35.
Samacheerkalvi.Guru 11th Maths Question 3.
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get Grade ‘A’ in the course.
Solution:
Let x be the marks obtained by Sunita in the fifth examination. Then,
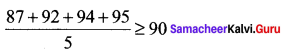
⇒ 368 + x ≥ 450 ⇒ x ≥ 450 – 368
⇒ x ≥ 82
Thus, Sunita must obtain marks greater than or equal to 82,
i. e., a minimum of 82 marks.
Samacheer Kalvi Guru 11th Maths Solution Question 4.
Find the pairs of ceonsecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
Solution:
Let x be the smaller of the two consecutive odd positive integers, then the other is x + 2 .
According to the given conditions.
x < 10, x + 2 < 10 and x + (x + 2) > 11
⇒ x < 10, x < 8
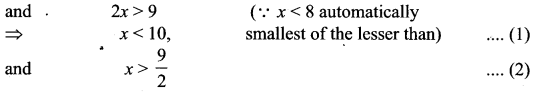
From (1) and (2), we get 9
\(\frac{9}{2}\) < x < 8
Also, x is an odd positive integer. x can take values 5 and 7.
So, the required possible pairs will be (x, x + 2) = (5, 7), (7, 9)
Samacheer Kalvi 11th Maths Question 5.
Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
Solution:
Let x be the smaller of the two consecutive even positive integers, then the other is x + 2. According to the given conditions.
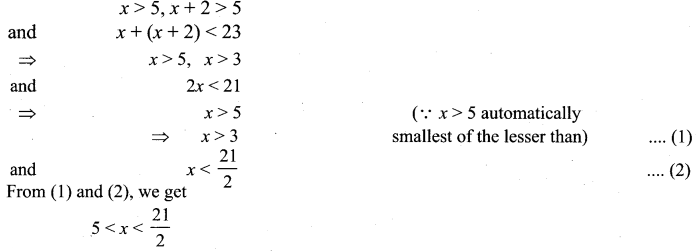
Also, x is an even positive integer.
x can take the values 6, 8 and 10.
So, the required possible pairs will be (x, x + 2) = (6, 8), (8, 10), (10, 12)
Maths Solution Class 11 Samacheer Kalvi Question 6.
Forensic Scientists use h = 61.4 + 2.3F to predict the height h in centimetres for a female whose thigh bone (femur) measures F cm. If the height of the female lies between 160 to 170 cm find the range of values for the length of the thigh bone?
Solution:
Given h = 61.4 + 2.3 F
Given h = 160 ⇒ 160 = 61.4 + 2.3 F
⇒ 2.3 F = 160 – 61.4 = 98.6
![]()
Given h = 170 ⇒ 170 = 61.4 + 2.3 F
⇒ 170 – 61.4 = 2.3 F
2.3F = 108.6
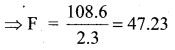
So the ranges of values are 42.87 < x < 47.23