Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.4

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.4

Question 1.
If f'(x) = 4x – 5 and f(2) = 1; find f(x)
Solution:
\(\int f^{\prime}(x) d x=\int(4 x-5) d x\)
f(x) = \(\frac{4 x^{2}}{2}\) – 5x + c
f(x) = 2x² – 5x + c
But f(2) = 1
2(2)² – 5(2) + c = 1
8 – 10 + c = 1
c = 3
Thus, f(x) = 2x² – 5x + 3

Question 2.
If f'(x) = 9x² – 6x and f(0) = -3; find f(x)
Solution:
f'(x) = \(\int\left(9 x^{2}-6 x\right) d x\)
f(x) = \(\frac{9 x^{3}}{3}-\frac{6 x^{2}}{2}\) + c
f(x) = 3x³ – 3x² + c
But f(0) = -3
3(0)³ – 3(0)² + c = -3
c = -3
Thus, f(x) = 3x³ – 3x² – 3
f(x) = 3(x³ – x² – 1)

Question 3.
If f'(x) = 12x – 6 and f(1) = 30, f'(1) = 5 find f(x)
Solution:
\(\)
f'(x) = \(\) – 6x + c
f'(x) = 6x² – 6x + c
But f'(1) = 5
6(1)² – 6(1) + c = 5
c = 5
f” (x) = 6x² – 6x + 5
\(\int f^{\prime \prime}(x) d x=\int\left(6 x^{2}-6 x+5\right) d x\)
f(x) = \(\frac{6 x^{3}}{3}-\frac{6 x^{2}}{2}\) + 5x + c
f(x) = 2x³ – 3x² + 5x + c
But f(1) = 30
2(1)³ – 3(1)² + 5(1) + c = 30
2 – 3 + 5 + c = 30
c = 26
f(x) = 2x³ – 3x² + 5x + 26

Question 4.
A ball is thrown vertically upward from the ground with an initial velocity of 39.2 mísec. If the only force considered is that attributed to the acceleration due to gravity, find
(i) how long will it take for the ball to strike the ground?
(ii) the speed with which will it strike the ground? and
(iii) how high the ball will rise?
Solution:
We know that

To find c₁ by substituting the initial conditions
x = 0 at t = 0 in the above equations,
We get C₁ = 0
∴ x = \(\frac{a t^{2}}{2}\) + 39.2t ………….. (3)
(i) While the ball strike the ground x = 0

(ii) The speed with which will it strike the ground?
At t = 8; (1) ⇒ v = -9.8(8) + 39.2
= -78.4 + 39.2
= -39.2
∴ The speed with which the ball will strike the ground is = 39.2 m/s
(iii) At maximum height v = 0
⇒ (2) ⇒ -9.8 t + 39.2 = 0
t = 4 sec
⇒ (3) ⇒ x = \(-\frac{9.8 \times 16}{2}\) + 39.2 × 4
= -78.4 + 156.8 = 78.4 m/s

Question 5.
A wound is healing in such a way that t days since Sunday the area of the wound has been decreasing at a rate of \(\frac{-6}{(t+2)^{2}}\)cm² per day where 0 < r ≤ 8. If on Monday the area of the wound was 1 .4 cm²
(i) What was the area of the wound on Sunday?
(ii) What is the anticipated area of the wound on Thursday if it continues to heal at the
same rate?
Solution:
Let A be the area of wound at time ‘t’.

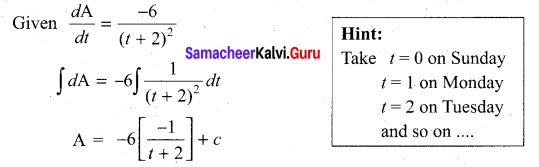
A = \(\frac{6}{t+2}\) + c
By the given, condition area of the wound on Monday is 1.4 cm²
⇒ A = 1.4; t = 1
⇒ 1.4 = \(\frac{6}{t+2}\) + c
1.4 = \(\frac{6}{3}\) + c
c = -0.6
∴ Area of wound at any day.
⇒ A = \(\frac{6}{t+2}\) – 0.6
(i) The area of a wound on Sunday
t = 0 ⇒ A = \(\frac{6}{2}\) – 0.6 = 3 – 0.6 = 2.4 cm²
(ii) The area of the wound on Thrusday
t = 4 ⇒ A = \(\frac{6}{6}\) – 0.6 = 1 – 0.6 = 0.4 cm²

Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.4 Additional Problems

Question 1.
If f'(x) = 2x – 7 and f(1) = 0 find f(x)
Solution:
Given f’ (x) = 2x – 7
⇒ f (x) = \(\int(2 x-7) d x\)
= x² – 7x + c
Given f(1) = 0 ⇒ 1 – 7 + c = 0
⇒ c = 6
So f(x) = x² – 7x + 6

Question 2.
Given f”(x) = 6x + 6, f'(0) = -5 and f(1) = 6 find f(x)
Solution:
f” (x) = 6x + 6
⇒ f ‘ (x) = (6x + 6) dx
= \(\frac{6 x^{2}}{2}\) + 6x + c
= 3x² + 6x + c
Given f ‘(0) = -5 ⇒ 0 + c = -5
⇒ c = -5
∴ f ‘(x) = 3x² + 6x – 5
So f(x) = \(\int\left(3 x^{2}+6 x-5\right) d x\)
= \(\frac{3 x^{3}}{3}+\frac{6 x^{2}}{2}\) – 5x + c
(i.e.,) f(x) = x³ + 3x² – 5x + c
Given f(1) = 6
⇒ 1 + 3 + 5 + c = 6
⇒ c – 1 = 6 ⇒ c = 7
So f(x) = x³ + 3x² – 5x + 7