Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.4

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.4

11th Maths Exercise 1.4 Solutions Question 1.
For the curve y = x³ given in Figure, draw
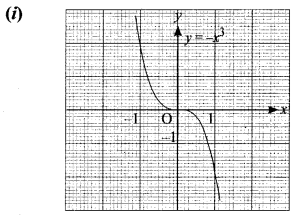
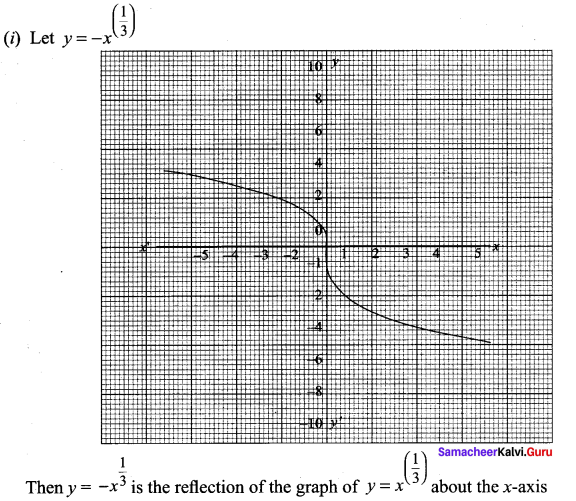
(i) r = -x³
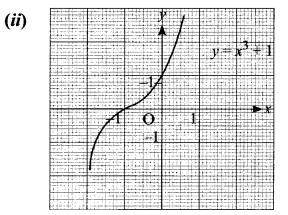
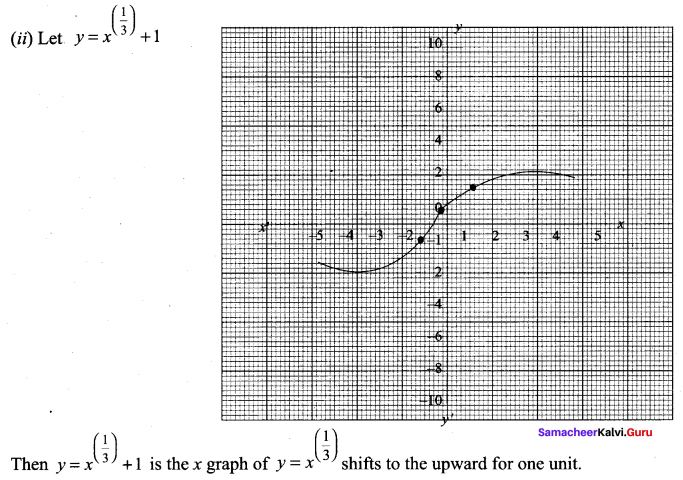
(ii) y = x³ + 1
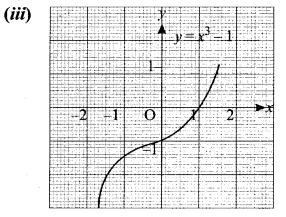
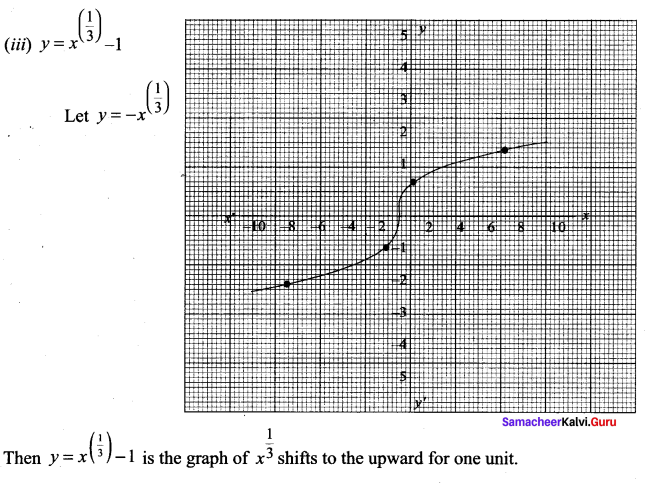
(iii) y = x³ – 1
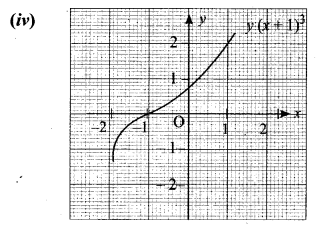
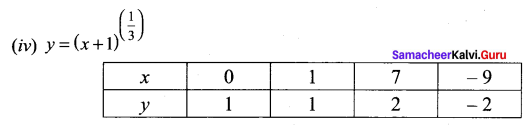
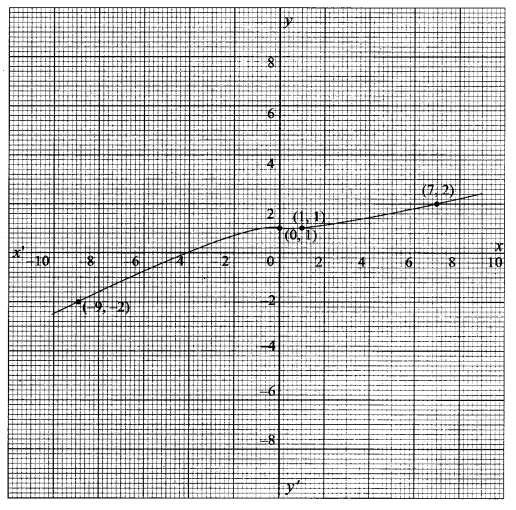
(iv) y = (x + 1)³ with the same scale.





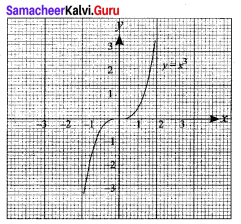
Solution:
(i) It is the reflection on y axis
(ii) The graph of y = x³ + 1 is shifted upward to 1 unit.
(iii) The graph of y = x³ – 1 is shifted downward to 1 unit.
(iv) The graph of y = (x + 1)³ is shifted to the left for 1 unit.

11th Maths Exercise 1.4 Answers Question 2.

Solution:

11th Maths Exercise 1.4 Question 3.
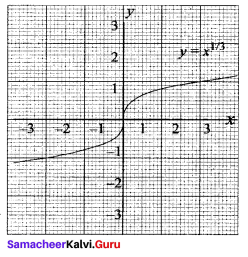
Graph the functions f(x) = x³ and g(x) = \(\sqrt[3]{x}\) on the same coordinate plane. Find fog and graph it on the plane as well. Explain your results.
Solution:

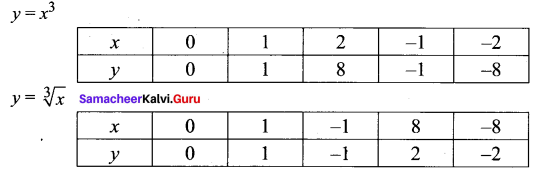
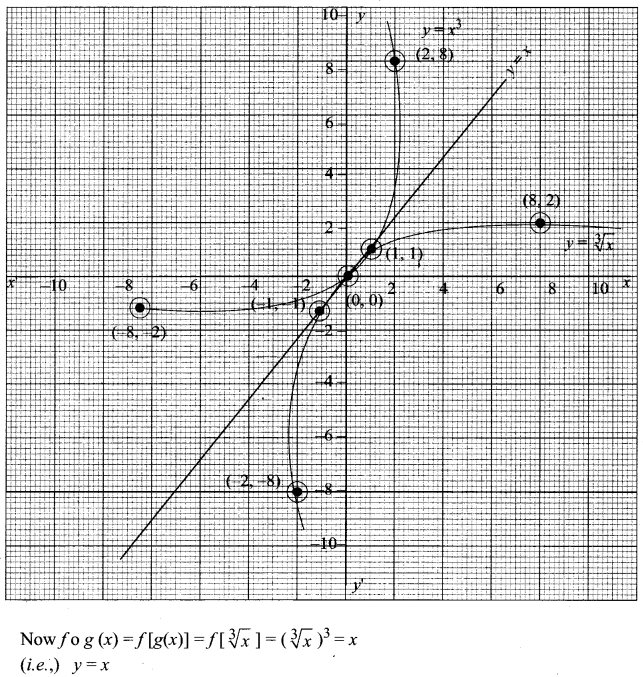
Exercise 1.4 Class 11 Maths Solutions Question 4.
Write the steps to obtain the graph of the function y = 3(x – 1)² + 5 from the graph y = x².
Solution:
Draw the graph of y = x²
To get y = (x – 1)² we have to shift the curve 1 unit to the right.
Then we have to draw the curve y = 3(x – 1)² and finally we have to draw y = 3(x – 1)² + 5

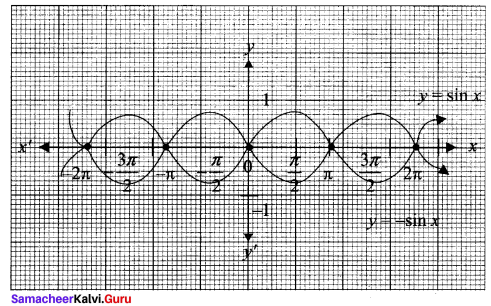
Samacheer Kalvi Guru 11th Maths Question 5.
From the curve y = sin x, graph the functions
(i) y = sin(-x)
(ii) y = -sin(-x)
(iii) y = sin (\(\frac{\pi}{2}\) + x) which is cos x
(iv) y = sin (\(\frac{\pi}{2}\) – x) which is also cos x (refer trigonometry)
Solution:
First we have to draw the curve y = sin x

(i) y = sin (-x) = – sin x = f(x)

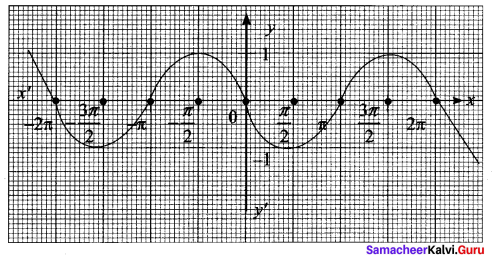
(ii) y = -sin(-x) = -[-sin x] = sin x

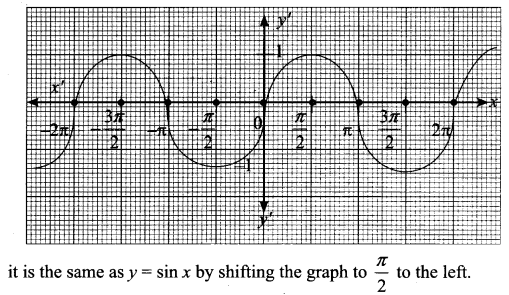
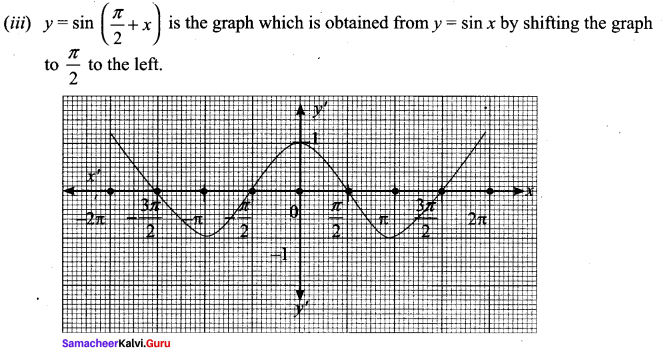
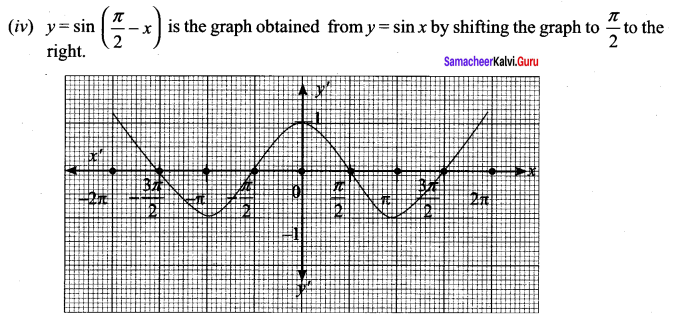
Maths Solution Class 11 Samacheer Kalvi Question 6.
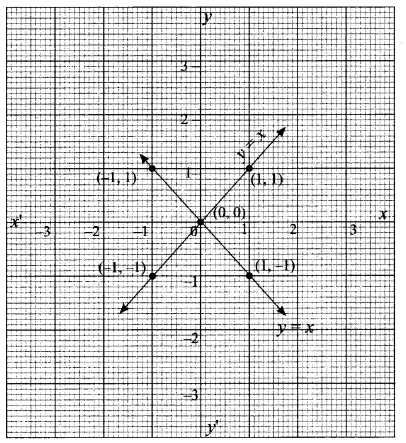
From the curve y = x, draw
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y = \(\frac{1}{2}\)x + 1
(v) 2x + y + 3 = 0. 2
Solution:
y = x

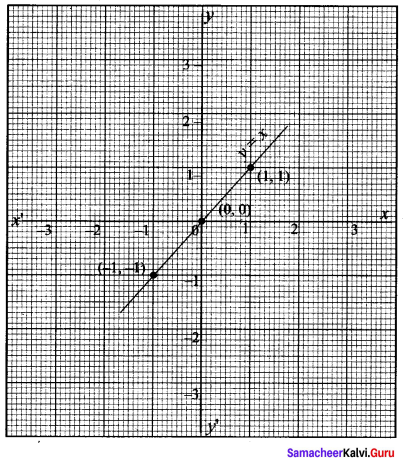
(i) y = -x

(ii) y = 2x


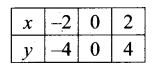
y = 2x the graph moves away the x-axis, as multiplying factor is 2 which is greater than one.

(iii) y = 2x + 1

(iv) y = 1/2x + 1


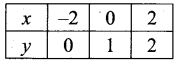
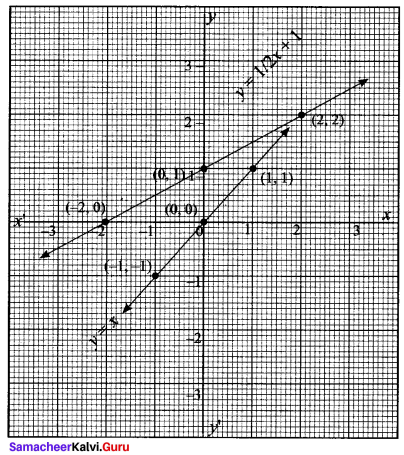
y = \(\frac{1}{2}\)x moves towards x – axis by a side factor \(\frac{1}{2}\) which is less than y = \(\frac{1}{2}\)x + 1 upwards by 1 unit.

(v) y = -2x – 3

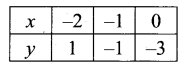
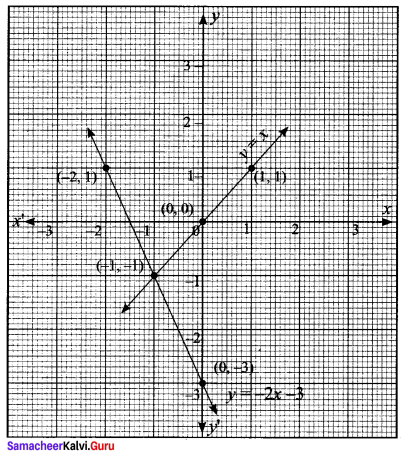
Samacheer Kalvi.Guru 11th Maths Question 7.
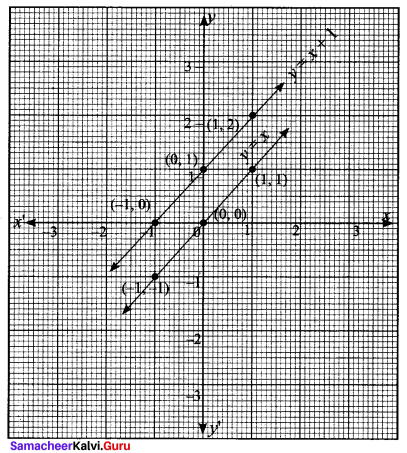
From the curve y = |x|, draw
(i) y= |x – 1| + 1
(ii) y = |x + 1| – 1
(iii) y = |x + 2| – 3.
Solution:
Given, y = |x|
If y = x

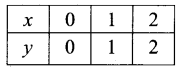
If y = -x

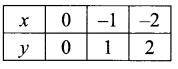
(i) y = |x – 1| + 1
y = x – 1 + 1
y = -x + 1 + 1 = x

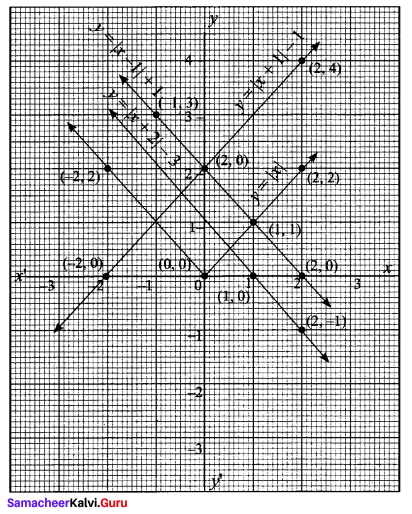
(ii) y = |x + 1| – 1
y = x + 1 – 1 = x
y = -x -1 – 1
y = -x – 2
y = – (x + 2)

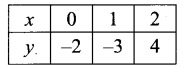
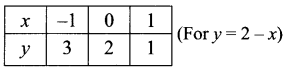
(iii) y = |x + 2| – 3
y = x + 2 – 3 ⇒ x – 1
y = -x – 2 + 3 = 1 – x
y = -(x – 1)

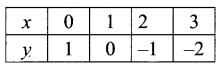
Question 8.
From the curves = sin x, draw y = sin |x| (Hint: sin(-x) = -sin x.)
Solution:
y = sin |x|
∴ y = sin x
∴ y = sin (-x) = – sin x
y = – sin x