Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.3

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.3

11th Maths Exercise 1.3 Answers Question 1.
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related toy if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.
Solution:
(i) A = {set of students in 11^th standard}
B = {set of sections in 11sup>th standard}
R : A ➝ B ⇒ x related to y
⇒ Every students in eleventh Standard must in one section of the eleventh standard.
⇒ It is a function.
Inverse relation cannot be a function since every section of eleventh standard cannot be related to one student in eleventh standard.

Exercise 1.3 Class 11 Maths State Board Question 2.
Write the values of f at – 4, 1, -2, 7, 0 if

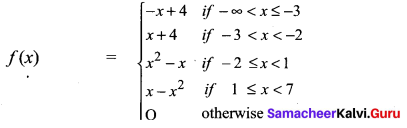
Solution:
f(-4) = -(-4) + 4 = 8
f(1) = 1 – 1² = 0
f(-2) = (-2)² – (-2) = 4 + 2 = 6
f(7) = 0
f(0) = 0

11th Maths Exercise 1.3 Question 3.
Write the values of f at -3, 5, 2, -1, 0 if

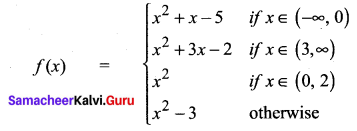
Solution:
f(-3) = (-3)² – 3 – 5 = 9 – 8 = 1
f(5) = (5)² + 3(5) – 2 = 25 + 15 – 2 = 38
f(2) = 4 – 3 = 1
f(-1) = (-1)² + (-1) – 5 = 1 – 6 = -5
f(0) = 0 – 3 = -3

11th Maths Exercise 1.3 Solutions Question 4.
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
(i) If A = {a, b, c] and/= {(a, c), (b, c), (c, b)};(f: A ➝ A).
(ii) If X = {x, y, z} and/= {(x, y), (x, z), (z, x)}; (f: X ➝ X).
Solution:
(i) f : A ➝ A

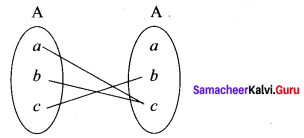
It is a function but it is not 1 – 1 and not onto function.

(ii) f : X ➝ X

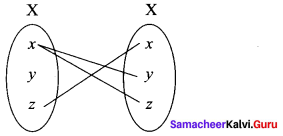
x ∈ X (Domain) has two images in the co-domain x. It is not a function.

11th Maths Exercise 1.3 Answers Samacheer Question 5.
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A ➝ B for each of the following:
(i) neither one-to-one nor onto.
(ii) not one-to-one but onto.
(iii) one-to-one but not onto.
(iv) one-to-one and onto.
Solution:
A = {1, 2, 3, 4}
B = {a, b, c, d}.

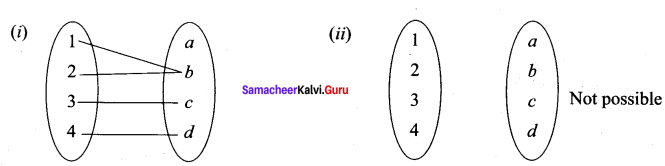
R = {(1, b) (2, b) (3, c) (4, d)} is not 1-1 and not onto

(iii) Not possible

(iv)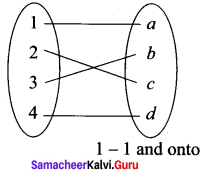

11 Maths Exercise 1.3 Question 6.
Find the domain of \(\frac{1}{1-2 \sin x}\)
Solution:

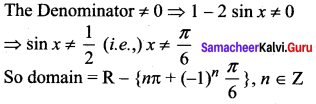
11th Maths Exercise 1.3 In Tamil Question 7.
Find the largest possible domain of the real valued function f(x) = \(\frac{\sqrt{4-x^{2}}}{\sqrt{x^{2}-9}}\)
Solution:

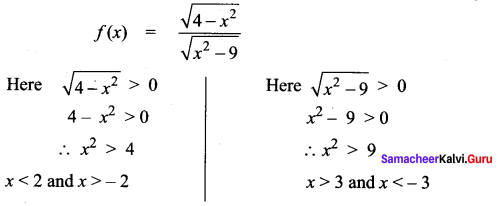
∴ No largest possible domain
The domain is null set

Samacheer Kalvi 11 Maths Solutions Question 8.
Find the range of the function \(\frac{1}{2 \cos x-1}\)
Solution:
The range of cos x is – 1 to 1

Exercise 1.3 Class 11 Maths Question 9.
Show that the relation xy = -2 is a function for a suitable domain. Find the domain and the range of the function.
Solution:
xy = – 2 ⇒ y = -2/x
which is a function
The domain is (-∞, 0) ∪ (0, ∞) and range is R – {0}

Samacheer Kalvi Guru 11th Maths Question 10.
If f, g : R ➝ R are defined by f(x) = |x| + x and g(x) = |x| – x, find gof and fog.
Solution:

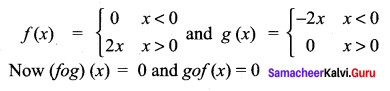
Samacheer Kalvi 11th Maths Question 11.
If f, g, h are real valued functions defined on R, then prove that
(f + g)oh = foh + goh. What can you say about fo(g + h) ? Justify your answer.
Solution:
Let f + g = k

= (f + g((h(x))
= f[h(x)] + g [h(x)]
= foh + goh
(i.e.,)(f + g)(o)h = foh + goh
fo(g + h) is also a function

Samacheer Kalvi Guru 11 Maths Question 12.
If f: R ➝ R is defined by f(x) = 3x – 5, prove that f is a bijection and find its inverse.
Solution:
P(x) = 3x – 5
Let y = 3x – 5 ⇒ 3x = y + 5

Samacheer Kalvi 11th Maths Book Back Answers Question 13.
The weight of the muscles of a man is a function of his body weight x and can be expressed as W(x) = 0.35x. Determine the domain of this function.
Solution:
W(x) = 0.35x
Since body weight x is positive and if it increases then W(x) also increase.
Domain is (0, ∞) i.e.,x > 0

Samacheerkalvi.Guru 11th Maths Question 14.
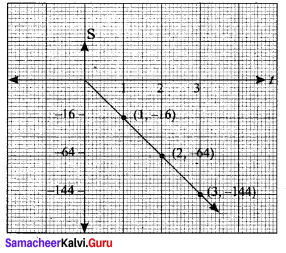
The distance of an object falling is a function of time t and can be expressed as s(t) = -16t². Graph the function and determine if it is one-to-one.
Solution:
s(t) = -16t²
Suppose S(t₁) = S(t₂)

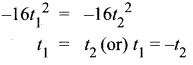
since time cannot be negative, we to take t₁ = t₂
Hence it is one-one.

t	0	1	2	3
s	0	-16	-64	-144

Samacheer Kalvi.Guru 11th Maths Question 15.
The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4m + 50 and S(m) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
Solution:
C – base cost,
S = fuel surcharge,
m = mileage
C(m) = 0.4 m + 50
S(m) = 0.03 m
Total cost = C(m) + S(m)
= 0.4 m + 50 + 0.03 m
= 0.43 m + 50
for 1600 miles
T(c) = 0.43 (1600) + 50 = 688 + 50 = ₹ 738

Samacheer Kalvi Class 11 Maths Question 16.
A salesperson whose annual earnings can be represented by the function A(x) = 30, 000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25, 000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1,50,00,000 worth of merchandise.
Solution:
A(x) = 30, 000 + 0.04x, where x is merchandise rupee value
S(x) = 25000 + 0.05 x
(A + S) (x) = A(x) + S(x)
= 30000 + 0.04x + 25000 + 0.05 x
= 55000 + 0.09x
(A + S) (x) = 55000+ 0.09x
They each sell x = 1,50,00,000 worth of merchandise
(A + S) x = 55000 + 0.09 (1,50,00,000)
= 55000 + 13,50,000
∴ Total income of family = ₹ 14,05,000

Samacheer Kalvi Class 11 Maths Solutions Question 17.
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee.
Solution:
f(x) = 1. 23x where x is number of American dollars.
g(y) = 50.50y where y is number of Singapore dollars.
gof(x) = g(f(x))
= g(1. 23x)
= 50.50 (1.23x)
= 62.115 x

Question 18.
The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 – x. Express his day revenue, total cost and profit on this meal as functions of x.
Solution:
cost of one meal = ₹ 100
Total cost = ₹ 100 (200 – x)
Number of customers = 200 – x
Day revenue = ₹ (200 – x) x
Total profit = day revenue – total cost
= (200 – x) x – (100) (200 – x)

Question 19.
The formula for converting from Fahrenheit to Celsius temperatures is \(y=\frac{5 x}{9}-\frac{160}{9}\)
Find the inverse of this function and determine whether the inverse is also a function.
Solution:

Question 20.
A simple cipher takes a number and codes it, using the function f(x) = 3x – 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines).
Solution:
f(x) = 3x – 4
Let y = 3x – 4

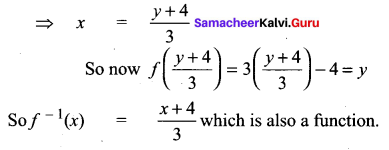
Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.3 Additional Questions

Question 1.
Find the domain and range of the function \(f(x)=\frac{1}{\sqrt{x-5}}\)
Solution:
Given that : f(x) \(f(x)=\frac{1}{\sqrt{x-5}}\)
Here, it is clear that / (x) is real when x – 5 > 0 ⇒ x > 5
Hence, the domain = (5, ∞)
Now to find the range put

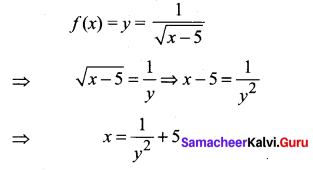
For x ∈ (5, ∞), y ∈ R⁺.
Hence, the range of f = R⁺.

Question 2.
If \(f(x)=\frac{x-1}{x+1}\), then show that

Solution:

Question 3.
Find the domain of each of the following functions given by:
\(f(x)=\frac{x^{3}-x+3}{x^{2}-1}\)
Solution:

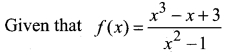
Here, f(x) is not defined if x² – 1 ≠ 0
(x – 1) (x + 1) ≠ 0
x ≠ 1, x ≠ -1
Hence, the domain of f = R – {-1, 1}

Question 4.
Find the range of the following functions given by
f(x) = 1 + 3 cos 2x
Solution:
Given that: f(x) = 1 + 3 cos 2x
We know that -1 ≤ cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3 ⇒ -3 + 1 ≤ 1 + 3 cos 2x ≤ 3 + 1
⇒ -2 ≤ 1 + 3 cos 2x ≤ 4 ⇒ -2 ≤ f(x) ≤ 4
Hence the range of f = [-2, 4]

Question 5.
Find the domain and range of the function \(f(x)=\frac{x^{2}-9}{x-3}\)
Solution:

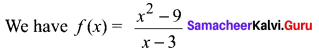
Domain off: Clearly f(x) is not defined for x – 3 = 0 i.e. x = 3.
Therefore, Domain (f) = R – {3}
Range off: Let f(x) = y. Then,

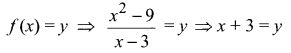
It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3}. Therefore, Range (f) = R {6}.

Question 6.
Find the range of the following functions given by f(x) = \(\frac{1}{2-\sin 3 x}\)
Solution: