Tamilnadu Samacheer Kalvi 11th Chemistry Notes Chapter 2 Quantum Mechanical Model of Atom Notes
Atom – The basic unit that makes up all matter.
Plaqck’s constant (h) – 6.626 x 10-34 Js.
Angular momentum – mvr ; mvr = nh/2π
Bohr’s atomic model – The electron is revolving around the nucleus in a certain fixed circular path called stationary orbit. The energies of electrons are quantized. Electron can revolve only in orbits in which the angular momentum (mvr) of the electron must be equal to an integral multiple of h/27r.
Radius of the nth orbit – rn = \(\frac{(0.529) \mathrm{n}^{2}}{\mathrm{Z}} \mathrm{A}\)
Energy of the nth orbit – \(E_{n}=\frac{(-13.6) Z^{2}}{n^{2}} e V \text { atom }^{-1} \text {(or) } \frac{(-1312.8) Z^{2}}{n^{2}} \text { kJ } m o l^{-1}\)
Louis de Broglie – All forms of matter showed dual character such as particle and wave.
de Broglie equation – λ = h/mv
Mass of an electron – 9.11 x 10-31 kg.
λ – de Broglie wavelength
Quantization of de Broglie concept – 2πr = nh/mv (or) mvr = nh/2π
Heisenberg’s uncertainty principle – Δx. Δp ≥ \(\frac{\mathrm{h}}{4 \pi}\) , where Ax = uncertainty in position.
Δp = uncertainty in momentum.
Bohr’s radius of 1st orbital – 0.529 Å
Schrodinger equation – \(\hat{\mathrm{H}} \psi=\mathrm{E} \psi\)
\(\hat{\mathrm{H}}\) = Hamiltonian operator.
\(\psi\) = wave function
E = Energy of the system
Schrodinger wave equation –
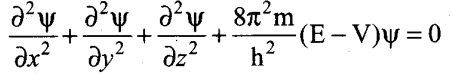
Quantum numbers – The set of four quantum numbers which can characterize an electron in an atom. They represent the energy level, sub shell, number of electron in an orbit, orientation of orbitals in space and the spin of the electron.
Atomic orbitals – Permitted energy values called eigen values which are known as atomic orbitals.
\(\)[\Psi]^{2}[/latex] – It is the probability of finding the electrons.
Node – The region where the probability density function reduces to zero is called nodal surface (or) a radial node.
Shapes of orbital –
s-orbital – spherical shape
p-orbital – dumb bell shape d-orbital – clover leaf
Effective nuclear charge – The net charge experienced by the electron.
Order of E.N.C – s>p>d>finan orbital.
Energy order in orbital – s<p<d<f.
Aufbau principle – “In the ground state of the atoms, the orbitals are filled in the order of their increasing energies”.
Pauli’s exclusion principle – “No two electrons in an atom can have the same set of values for alf.four quantum numbers.”
Types of quantum numbers – Principal quantum number (n), azimuthal quantum number (i), magnetic quantum number (m) and spin quantum number (s).
| Principal quantum number (n): | Azimuthal quantum number (l) | Magnetic quantum number (m): | Spin quantum number (s): |
| (i)It represents the energy level in which electron is present | It represents the subshell in which electron is present | It represents different orientation of orbitals in space | It represents the spin of the electron |
| (ii) Maximum number of electrons that can be accommodated in the shell is 2n2. | Maximum number of electrons that can be accommodated in subshell is 2(2l+1). | The magnitude of angular momentum is determined. | Electron revolves in clockwise and anti-clockwise directions. |
| v _-(1312.8) Z2 /n2 kJ mol-1. | It is used to calculate the orbital angular momentum by the formula |
If l= 1, m = -1, 0, +1 | s values are + 1/2 (or) – 1/2 |
| It represents the distance of the electron from the nucleus. | 1 = 0, 1,2, 3 Subshell = s, p, d, f No. of electrons = 2, 6, 10, 14 | ||
| n = 1,2,3,4 . main shell = k, l, m, n No. of electrons = 2, 8, 18, 32 |
Hund’s rule of maximum multiplicity – It states that electron pairing in the degenerate orbitals does not take place until all the available orbitals contains one electron each.
Electronic configuration – The distribution of electrons into various orbitals of an atom is called its electronic configuration.
Exchange energy – During the exchanging process of two or more electrons with the same spin present in degenerate orbitals, the amount of energy released is called exchange energy.