Samacheer Kalvi 10th Maths Guide Chapter 4 வடிவியல் Unit Exercise 4

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 4 வடிவியல் Unit Exercise 4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 4 வடிவியல் Unit Exercise 4

கேள்வி 1.
கொடுக்கப்பட்ட படத்தில் BD⊥AC மற்றும் CE⊥AB, எனில்
i) ∆AEC ~ ∆ADB
\(\frac{\mathrm{CA}}{\mathrm{AB}}=\frac{\mathrm{CE}}{\mathrm{DB}}\) நிரூபிக்கவும்.

தீர்வு :
i) ∆AECமற்றும் ∆ADB இவற்றில்
∠AEC = ∠ADB = 90, ∠A பொது
∆AEC ~ ∆ADB (AA விதிமுறைப்படி)
ii) ∆AEC ~ ∆ADB [ (i)ன் படி)
\(\frac{\mathrm{CA}}{\mathrm{AB}}=\frac{\mathrm{CE}}{\mathrm{DB}}\)

கேள்வி 2.
கொடுக்கப்பட்ட படத்தில் AB||CD| |EF AB = 6 செ.மீ , CD = xசெ .மீ, EF = 4 செ.மீ, BD = 5செ.மீ மற்றும் DE = y செ.மீ எனில் , மற்றும் புன் மதிப்பு காண்க.
தீர்வு :

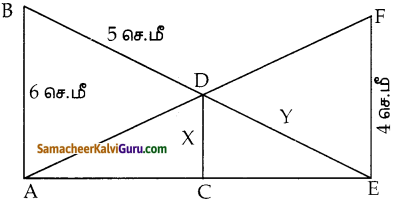
WkT, இரு தூண்களின் உச்சியிலிருந்து எதிரேயுள்ள தூண்களின் அடிக்கு வரையப்படும் கோடுகள் சந்திக்கும் புள்ளியின் உயரமானது \(\frac{a b}{a+b}\) ஆகும்.

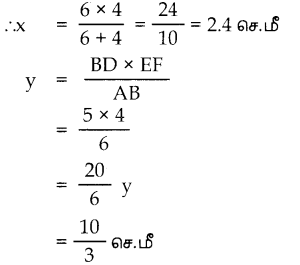
கேள்வி 3.
O ஆனது முக்கோணம் ABC ,யின் உள்ளே அமைந்த ஒரு புள்ளி ஆகும். ∠AOB , ∠BOC மற்றும் COA யின் இருசமவெட்டிகள், பக்கங்கள் AB, BC மற்றும் CA வை முறையே D, E மற்றும் Fல் சந்திக்கின்றன எனில், AD * BEX CF= DBX ECX FA எனக் காட்டுக
தீர்வு :

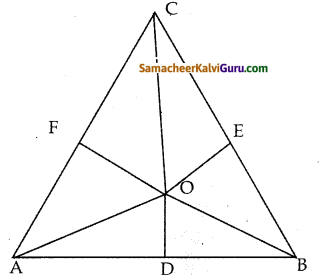
Δ AOB, OD ஆனது ∠AOB ன் இருசமவெட்டி
∴ \(\frac{\mathrm{OA}}{\mathrm{OB}}=\frac{\mathrm{AD}}{\mathrm{DB}}\) ————- (1)
Δ BOC, OE ஆனது ∠BOC ன் இருசமவெட்டி
∴ \(\frac{\mathrm{OB}}{\mathrm{OC}}=\frac{\mathrm{BE}}{\mathrm{EC}}\) —————– (2)
Δ COA, OF ஆனது ∠COA ன் இருசமவெட்டி
∴ \(\frac{\mathrm{OC}}{\mathrm{OA}}=\frac{\mathrm{CF}}{\mathrm{AF}}\)—————- (3)
(1) x (2) x (3)

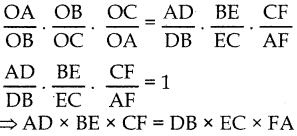
கேள்வி 4.
கொடுக்கப்பட்ட முக்கோணம் ABC யில் AB = ACஆகும். AD = AE என இருக்குமாறு D மற்றும் என்ற புள்ளிகள் முறையே பக்கங்கள் AB மற்றும் AC-யின் மீது அமைந்துள்ளன. B,C,E மற்றும் D என்ற புள்ளிகள் ஒரே வட்டத்தில் அமையும் எனக் காட்டுக

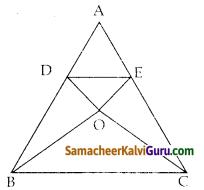
தீர்வு :
கணக்கின் படி. AB = AC
⇒ ∠B = ∠C
AD + DB = AE + EC
⇒ BD = EC[: AD = AE]
∴ DE || BC
AEC என்பது நேர்க்கோடு என்பதால்

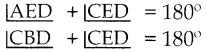
எதிர்கோணங்களின் கூடுதல் 180°
∴ BCED என்பது விட்ட நாற்கரம் ஆகும். ..
∴ B, C, E மற்றும் D என்ற
புள்ளிகள் ஒரு வட்டத்தில் அமையும்.

கேள்வி 5.
இரண்டு தொடர்வண்டிகள் ஒரே நேரத்தில் ஒரு தொடர்வண்டி நிலையத்திலிருந்து புறப்படுகின்றன. முதல் வண்டி மேற்கு நோக்கியும், இரண்டாவது வண்டி வடக்கு நோக்கியும் செல்கின்றன. முதல் தொடர்வண்டி 20 கி.மீ/மணி வேகத்திலும், இரண்டாவது வண்டி 30கி.மீ/மணி வேகத்திலும் செல்கின்றன. இரண்டு மணி நேரத்திற்குப் பின்னர் அவைகளுக்கு இடையேயுள்ள தொலைவு எவ்வளவு?
தீர்வு :
இரண்டு மணி நேரத்திற்குப் பின்னர் முதல் மற்றும் இரண்டாம் தொடர்வண்டிகள் கடந்து சென்ற தொலைவு 40 கி.மீ மற்றும் 60கி.மீ.

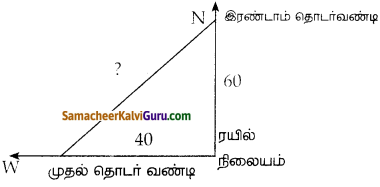
அவைகளுக்கு இடைப்பட்ட

கேள்வி 6.
BC யின் மையப்புள்ளி D மற்றும் AE ⊥ BC. BC = a, AC = b, AB = C, ED = x, AD = P மற்றும் AE = h, எனில், (i) b² = p² + ax + \(\frac{a^{2}}{4}\)
(ii) c² = p² – ax + \(\frac{a^{2}}{4}\)
(iii) b² + c² = 2p² + \(\frac{a^{2}}{2}\) என நிரூபிக்க.

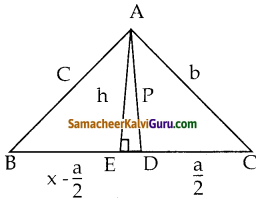
கணக்கின் படி, D என்பது BC ன் மையப்புள்ளி
CD = BD = \(\frac{a}{2}\) மற்றும் BE = x – \(\frac{a}{2}\)
∆AED & P² = h² + x² —— (1)
(பிதாகரஸ் தேற்றப்படி)

i) ∆AEC, ல் b² = h² + (x + \(\frac{a}{2}\) )²
= h² + x² + ax + \(\frac{a^{2}}{4}\)
= p² + ax + \(\frac{a^{2}}{4}\) (1) லிருந்து

ii) ∆AEB ல், C² = h² + (x – \(\frac{\mathrm{a}}{2}\) )²
= h² + x² – ax + \(\frac{a^{2}}{4}\)
= p² – ax + \(\frac{a^{2}}{4}\) (1) லிருந்து
(iii) (i) & (ii) ஐ கூட்ட
b² + c² = p² + ax + \(\frac{a^{2}}{4}\) + p² – ax + \(\frac{a^{2}}{4}\)
= 2p² + \(\frac{a^{2}}{2}\)

கேள்வி 7.
2 மீ உயரமுள்ள மனிதர் ஒரு மரத்தின் உயரத்தைக் கணக்கிட விரும்புகிறார். மரத்தின் அடியிலிருந்து 20 மீ தொலைவில் B என்ற புள்ளியில் ஒரு கண்ணாடி கிடைமட்டமாக மேல் நோக்கி வைக்கப்படுகிறது. கண்ணாடியிலிருந்து 4 மீ தொலைவில் C என்ற புள்ளியில் நிற்கும் மனிதர் மரத்தின் உச்சியின் பிரதிபலிப்பைக் கண்ணாடியில் காண முடிகிறது எனில், மரத்தின் உயரத்தைக் காண்க. (மரத்தின் அடி, கண்ணாடி, மனிதர் ஒரே நேர்க்கோட்டில் உள்ளதாகக் கொள்க).
தீர்வு :

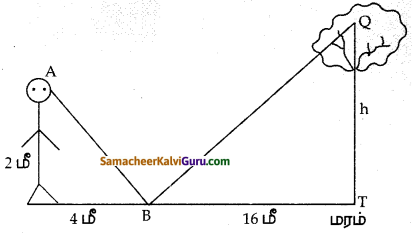
படத்திலிருந்து ∆ACB ~ ∆QTB
∴ \(\frac{\mathrm{TQ}}{\mathrm{AC}}=\frac{\mathrm{TB}}{\mathrm{BC}}\)
⇒ \(\frac{h}{2}=\frac{16}{4}\)
∴ h = \(\frac{16}{4}\) x 2
= 8
மரத்தின் உயரம் = 8 + 2
= 10மீ

கேள்வி 8.
30 அடி உயரமுள்ள ஒரு தூணின் அடிப்பகுதியிலிருந்து 8 அடி உயரமுள்ள ஒரு ஈமு கோழி விலகி நடந்து செல்கிறது. ஈமு கோழியில் நிழல் அது நடந்து செல்லும் திசையில் அதற்கு முன் விழுகிறது. ஈமு கோழியின் நிழலின் நீளத்திற்கும், ஈமு தூணிலிருந்து இருக்கும் தொலைவிற்கும் இடையே உள்ள தொடர்பைக் காண்க.

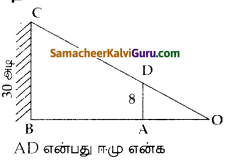
தேல்ஸ் தேற்றப்படி,
\(\frac{O A}{O B}=\frac{A D}{B C}\)
∴ ⇒ \(\frac{x}{x+y}=\frac{8}{30}\)
இருபுறமும் தலைகீழ் காண

கேள்வி 9.
A மற்றும் B என்ற புள்ளிகளில் இரு வட்டங்கள் வெட்டிக்கொள்கின்றன. ஒரு வட்டத்தின் மீதுள்ள புள்ளி P யிலிருந்து வரையப்படும் PAC மற்றும் PBD என்ற கோடுகள் இரண்டாவது வட்டத்தினை முறையே ( மற்றும் D யில் வெட்டுகின்றன எனில் CD யானது P வழியே வரையப்படம் தொடுகோட்டிற்கு இணை என நிரூபிக்கவும். தீர்வு :
MPஎன்பது புள்ளி P ல் வட்டத்தின் தொடுகோடு என்க.
AB இணை

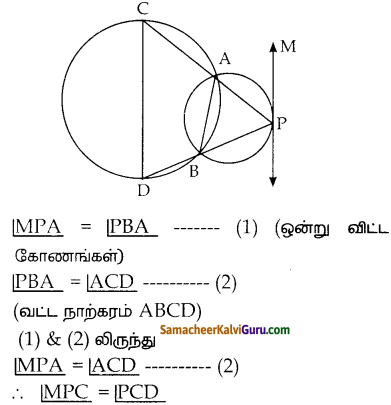
இவைகள் ஒன்று விட்ட உள்கோணங்களின் சோடிகள்.
∴ MP || CD

கேள்வி 10.
ABC என்ற ஒரு முக்கோணத்தின் பக்கங்கள் AB, BC, AC யின் (அல்லது பக்கங்களின் நீட்சி) மீது முறையே D,E,F என்ற புள்ளிகள் உள்ள ன. AD : DB = 5:3, BE:EC = 3:2 மற்றும் AC = 21. எனில், கோட்டுத்துண்டு CF யின் நீளம் காண்க.
தீர்வு :

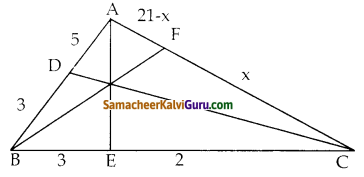
சீவாஸ் தேற்றப்படி
\(\frac{\mathrm{AD}}{\mathrm{DB}} \times \frac{\mathrm{BE}}{\mathrm{EC}} \times \frac{\mathrm{CF}}{\mathrm{FA}}\) = 1
⇒ \(\frac{5}{3} \times \frac{3}{2} \times \frac{x}{21-x}\) = 1
⇒ 5x = 2 (21 – x)
= 42 – 2x
7x = 42
x = 6
∴ CF = 6