Samacheer Kalvi 10th Maths Guide Chapter 4 வடிவியல் Ex 4.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 4 வடிவியல் Ex 4.4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 4 வடிவியல் Ex 4.4

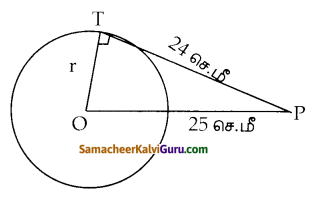
கேள்வி 1.
வட்டத்தின் மையத்திலிருந்து 25 செ.மீ தொலைவில் உள்ள P என்ற புள்ளியிலிருந்து வட்டத்திற்கு வரையப்பட்ட தொடுகோட்டின் நீளம் 24 செ.மீ எனில், வட்டத்தின் ஆரம் என்ன ?
தீர்வு :
r = \(\sqrt{25^{2}-24^{2}}\)
= \(\sqrt{625-576}\)
= \(\sqrt{49}\)
= 7செ.மீ

கேள்வி 2.
செங்கோண முக்கோணம் LMN யில் ∠L = 90° ஆகும். ஒரு வட்டமானது செங்கோண முக்கோணத்தின் உள்ளே அதன் பக்கங்களைத் தொடுமாறு வரையப்படுகிறது. செங்கோணத்தைத் தாங்கும் பக்கங்களின் நீளங்கள் 6 செ.மீ மற்றும் 8 செ.மீ எனில், வட்டத்தின் ஆரம் காண்க.
தீர்வு :

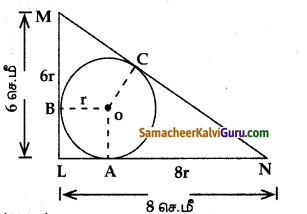
ΔLMN ல். பிதாகரஸ் தேற்றப்படி
MN² = LN² + LM²
= 8² + 6² = 100
MN = 10 செ.மீ
இப்பொழுது
ΔLMN ன் பரப்பு = ΔOLM ன் பரப்பு + ΔOMN ன் பரப்பு + ΔONLன் பரப்பு
\(\frac { 1 }{ 2 }\) x 6 x 8 = \(\frac { 1 }{ 2 }\)x 6r + \(\frac { 1 }{ 2 }\) x 10r + \(\frac { 1 }{ 2 }\) x 8r
24 = 3r + 5r + 4r
12r = 24
r = 2 செ.மீ
∴ வட்டத்தின் ஆரம் 2 செ.மீ

கேள்வி 3.
படத்தில் காட்டியுள்ளபடி, 8 செ.மீ, 10 செ.மீ மற்றும் 12 செ.மீ பக்கங்கள் உடைய முக்கோணத்தினுள் ஒரு வட்டம் அமைந்துள்ளது எனில், AD, BE மற்றும் CF ஐக் காண்க.
தீர்வு :
படத்திலிருந்து
x + y = 12 —- (1)
y + z = S —- (2)
x + z == 10 —- (3)
இப்பொழுது


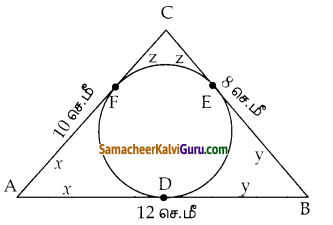
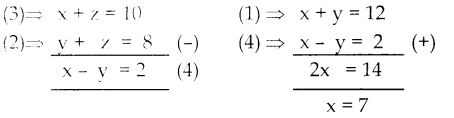
x = 7 = 2 ஐ ( 1 ), ல் பிரதியிட y = 5
x = 7 ஐ (3)ல் பிரதியிட z = 3
AD = 7 செ.மீ
BE = 5 செ.மீ
CF = 3 செ.மீ

கேள்வி 4.
O வை மையமாக உடைய வட்டத்திற்கு P யிலிருந்து வரையப்பட்ட தொடுகோடு PQ, QOR ஆனது விட்டம் ஆகும். வட்டத்தில் |∠POR = 120° எனில், ∠OPQ – ஐக் காண்க.
தீர்வு :

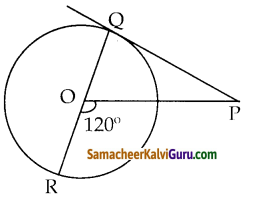
படத்திலிருந்து ∠QOP = 60° [: QOR நேர்க்கோடு]
மற்றும் ∠PQO = 90° [: தொடுகோடு)
∠OPQ = 180° – (∠QOP + ∠PQO )
= 180° – (60 + 90)
= 180 – 150
= 30°

கேள்வி 5.
தொடுகோடு STவட்டத்தினை B என்ற புள்ளியில் தொடுகிறது. ∠ABT = 65° AB என்பது ஒரு நாண் எனில், ∠AOB ஐ காண்க. இதில் ‘O’ என்பது வட்டத்தின் மையம் ஆகும்.
தீர்வு :

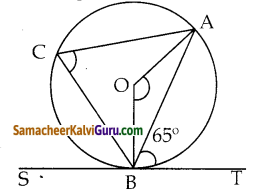
நாண் AB க்கு மாற்று வட்டத்துண்டில் புள்ளி C யை குறிக்க.
கணக்கின் படி ∠ABT = 650
∴ ∠ACB = 65° [மாற்று வட்டத்துண்டு தேற்றம் ]
∴ ∠AOB = 2 x 65
= 130°

கேள்வி 6.
கொடுக்கப்பட்ட படத்தில் 0 – வை மையமாக உடைய வட்டத்தின் ஆரம் 5 செ.மீ ஆகும். T யானது OT = 13 செ.மீ என அமைந்த ஒரு புள்ளி மற்றும் OT – யானது வட்டத்தை E யில் வெட்டுகிறது. வட்டத்தில் E என்ற புள்ளியின் வழியாகச் செல்லும் ஒரு தொடுகோடு AB எனில், AB யின் நீளம் காண்க.
தீர்வு :

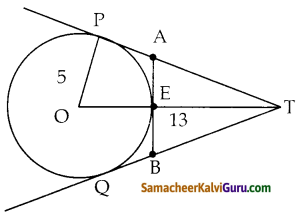
ΔOPT, ல் PT = \(\sqrt{13^{2}-5^{2}}\)
= \(\sqrt{169-25}\)
= \(\sqrt{144}\)
= 12 செ.மீ
PA = x என்க
∴ AB = x, AT = 12 – X மற்றும் ET = 8
ΔAET, ல் ∠ABT = 90
∴ (12 – x)² = x² + 8² (பிதாகரஸ் தேற்றம்)
= 144 + x² – 24x = x² + 64
= 24x = 80
x = \(\frac{10}{3}\)
∴ AB ன் நீளம் = 2 x AE
= 2 x \(\frac{10}{3}\)
= \(\frac{20}{3}\) செ.மீ

கேள்வி 7.
இரண்டு பொது மைய வட்டங்களில், 16 செ.மீ நீளமுடைய பெரிய வட்டத்தின் நாணானது 6 செ.மீ ஆரமுள்ள சிறிய வட்டத்திற்குத் தொடுகோடாக அமைந்தால், பெரிய வட்டத்தின் ஆரம் காண்க.
தீர்வு :

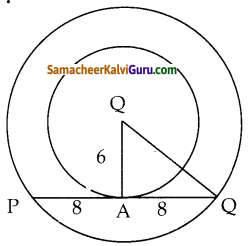
கணக்கின் படி PQ = 16 செ.மீ
∴ AQ = 8 செ.மீ [ தேற்றம்)
ΔOAR,ல் OQ² = OA² + AQ²
= 6² + 8²
= 36 + 64
= 100
∴ OQ = 10 செ.மீ
∴ பெரிய வட்டத்தின் ஆரம் 10 செ.மீ.

கேள்வி 8.
O மற்றும் 0′-ஐ மையப்புள்ளிகளாகக் கொண்ட இரு வட்டங்களின் ஆரங்கள் முறையே 3 செ.மீ மற்றும் 4 செ.மீ ஆகும். இவை இரண்டும் P, Q என்ற புள்ளிகளில் வெட்டிக்கொள்கின்றன. OP மற்றும் OP ஆகியவை வட்டங்களின் இரு தொடுகோடுகள் எனில், பொது நாண் PQ யின் நீளம் காண்க.
தீர்வு :

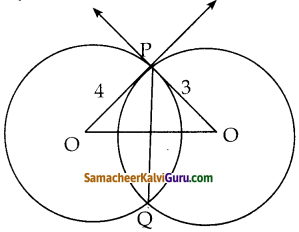
படத்தில்
∠OPO = 90°
00 = \(\sqrt{4^{2}+3^{2}}\) = 5
OʻL = x, என்க OL = 5 – x
PL² = 4² – x² = 3² – (5 – x)²
16 – x² = 9² – (25 + x² – 10x)
16 = – 16 + 10x
10x = 32
x = \(\frac{32}{10}\)
x = 3.2 செ.மீ
∴ PL = \(\sqrt{4^{2}-(3.2)^{2}}\)
= \(\sqrt{16-10.04}\)
= \(\sqrt{5.76}\)
= 2.4
∴ PQ = 2 x 2.4
= 4.8 செ.மீ

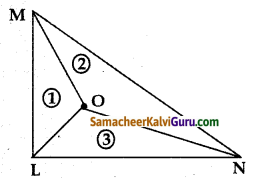
கேள்வி 9.
ஒரு முக்கோணத்தின் கோண இருசம் வெட்டிகள் ஒரு புள்ளியின் வழியாகச் செல்லும் எனக் காட்டுக.
தீர்வு :

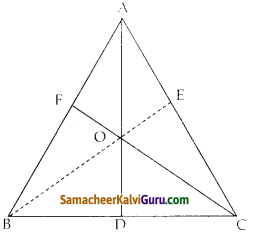
முக்கோணம் ABCல் AD , BE என்பன முறையே ∠A, ∠B இருசம் வெட்டிகள் என்க
AD , BE ம் O வில் சந்திக்கின்றன என்க நிரூபிக்கவேண்டியது;
CF,ஆ எது ∠C ன் இருசம வெட்டி எனவும் C வழியாக செல்கிறது எனவும் நிரூபிக்க வேண்டும்
(ie) \(\frac{\mathrm{AO}}{\mathrm{OD}}=\frac{A C}{\mathrm{CD}}\)
நிரூபணம் :
ΔABC ல், AD ஆனது ∠Aன் இருசமவெட்டி
⇒ \(\frac{B D}{D C}=\frac{A B}{B C}\)
(கோண இருசவெட்டி தேற்றம்) — (1)
ΔABD ல், BO ஆனது ∠Bன் இருசமவெட்டி
\(\frac{\mathrm{AO}}{\mathrm{OD}}=\frac{\mathrm{AB}}{\mathrm{BD}}\)——(2)
(1) லிருந்து \(\frac{A C}{D C}=\frac{A B}{B D}\) ———(3)
∴ (2) & (3) லிருந்து
\(\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{AO}}{\mathrm{OD}}\)\
(ie) CO ஆனது ∠Cன் இருசமவெட்டி
∴ ஒரு முக்கோணத்தின் கோண இருசமவெட்டிகள் ஒரு புள்ளியின் வழியாகச் செல்லும்

கேள்வி 10.
படத்தில் உள்ளவாறு ஒரு முக்கோண வடிவக் கண்ணாடி ஜன்னலை முழுமையாக உருவாக்க ஒரு சிறிய கண்ணாடித்துண்டு ஒரு கலை நிபுணருக்குத் தேவைப்படும். மற்ற கண்ணாடி துண்டுகளின் நீளங்களைப் பொருத்து அவருக்குத் தேவையான கண்ணாடித் துண்டின் நீளத்தைக் கணக்கிடவும்.
தீர்வு :

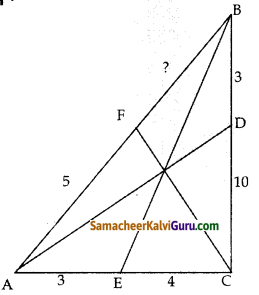
O என்பது மூன்று கோணங்களின்
இருசமவெட்டிகளும் சந்திக்கும் புள்ளி என்க.
படத்திலிருந்து
\(\frac{B F}{F A}=\frac{O B}{O A}\) ……………. (1)

கேள்வி 11.
P யை மையமாகக் கொண்ட 3.4 செ.மீ ஆரமுள்ள ஒரு வட்டத்திற்கு R என்ற புள்ளியில் தொடுகோடு வரைக. தீர்வு :

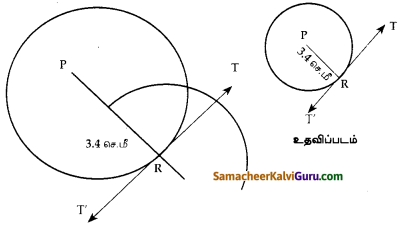
வரைமுறை :

1. 3.4 செ.மீ ஆரமுள்ள வட்டம் வரைக.மையம் P
2. வட்டத்தின் பரிதியின் மீது R என்ற புள்ளியை குறி
3. TT’PR வரைக.
4. TT’ என்பது தேவையான தொடுகோடு ஆகும்.

கேள்வி 12.
4.5 செ.மீ ஆரமுள்ள வட்டம் வரைக. வட்டத்தின் மீது ஏதேனும் ஒரு புள்ளிக்கு மாற்று வட்டத்துண்டு தேற்றத்தினைப் பயன்படுத்தித் தொடுகோடு வரைக.
தீர்வு :

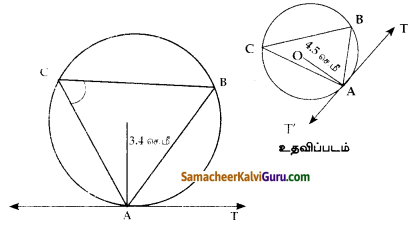
வரைமுறை :

1. O வை மையமாகக் கொண்டு 4.5 செ.மீ ஆரமுள்ள வட்டம் வரைக.
2. வட்டத்தின் மேல் A என்ற புள்ளி வழியாக AB ன் நாண் வரைக.
3. AB க்கு மாற்று வட்டத்தின் C என்ற புள்ளியை குறி
4. C, AB இவற்றை இணை
5. A வழியாக TT’ தொடுகோடு வரைக. ∠TAB = ∠BCA
6. TT’ என்பது தேவையான தொடுகோடு ஆகும்.

கேள்வி 13.
5செ.மீ ஆரமுள்ள வட்டத்தின் மையத்திலிருந்து 10செ. மீ தொலைவிலுள்ள புள்ளியிலிருந்து
வட்டத்திற்குத் தொடு கோடுகள் வரையவும். மேலும் தொடுகோட்டின் நீளங்களைக் கணக்கிடுக.
தீர்வு :

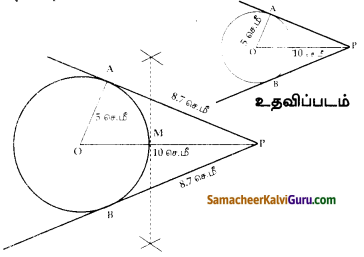
வரைமுறை :

1. O வை மையமாகக் கொண்டு 5 செ.மீ ஆரமுள்ள வட்டம் வரைக.
2. OP = PO செ.மீ வரைக.
3. OP. மையக்குத்து கோடு வரைக. அது OP ஐ Mல் சந்திக்கிறது
4. M யை மையமாகவும், OM ஐ ஆரமாகவும் கொண்டு வட்டம் வரைக.
5. இரண்டு விட்டங்களும் A,B ல் சந்திக்கும்
6. PA, PB யை இணை .
7. தொடுகோட்டின் நீளம் PA = PB = 8.7 செ.மீ

கேள்வி 14.
4 செ.மீ ஆரமுள்ள வட்டம் வரைந்து அதன் மையத்திலிருந்து 11 செ.மீ தொலைவிலுள்ள ஒரு புள்ளியைக் குறித்து, அப்புள்ளியிலிருந்து வட்டத்திற்கு இரண்டு தொடுகோடுகள் வரைக.
தீர்வு:

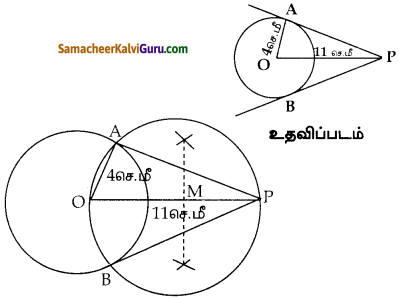
வரைமுறை :

1. Oவை மையமாகக் கொண்டு 5 செ.மீ ஆரமுள்ள வட்டம் வரைக
2. OP = 10 செ.மீ வரைக.
3. OPக்கு மையக்குத்துகோடு. OP ஐ M ல் சந்திக்கிறது
4. M யை மையமாகவும். OM ஐ ஆரமாகவும் கொண்டு வட்டம் வரைக.
5. இரு வட்டங்களும் வெட்டும் புள்ளிகள் A,B
6. AP, BP என்பன இரு தொடுகோடுகளாகும்

கேள்வி 15.
6 செ.மீ விட்டமுள்ள வட்டம் வரைந்து வட்டத்தின் மையத்திலிருந்து 5 செ.மீ தொலைவிலுள்ள ஒரு புள்ளியைக் குறிக்கவும். அப்புள்ளியிலிருந்து வட்டத்திற்குத் தொடுகோடுகள் வரைந்து, தொடுகோட்டின் நீளங்களைக் கணக்கிடுக.
தீர்வு :

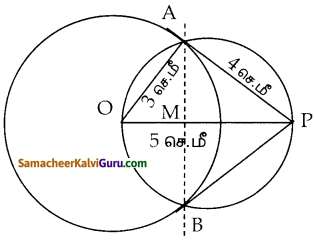
வரைமுறை :

1. Oவை மையமாகக் கொண்டு 3 செ.மீ ஆரமுள்ள விட்டம் வரைக.
2. OP = 5 செ.மீ வரைக
3. OP, யை இருசம கூறிடுக. அது OP யை வெட்டும் புள்ளி அ என்க.
4. M யை மையமாகவும், OM ஐ ஆரமாகவும் கொண்டு வட்டம் வரைக.
5. இரு வட்டங்களும் வெட்டும் புள்ளிகள் A, B
6. AP, BP யை இணை .
7. தொடுகோட்டின் நீளம் AP = BP = 4 செ.மீ

கேள்வி 16.
O வை மையமாகக் கொண்ட 3.6 செ.மீ ஆரமுள்ள வட்டம் வரைக. வட்டத்தின் மையத்திலிருந்து 7.2 செ.மீ தொலைவிலுள்ள P என்ற புள்ளியைக் குறித்து அப்புள்ளியிலிருந்து வட்டத்திற்குத் தொடுகோடுகள் வரைக.
தீர்வு :

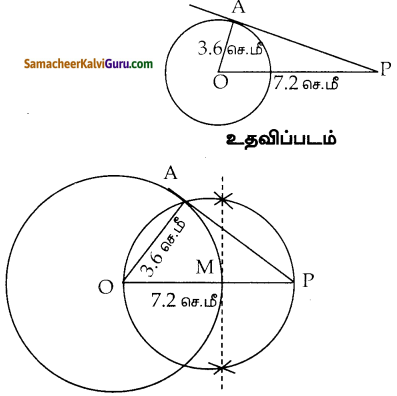
வரைமுறை :

1. Oவை மையமாகக் கொண்டு 3.6 செ.மீ ஆரமுள்ள வட்டம் வரைக
2. OP = 7.2 செ.மீ வரைக
3. OPயை இருசமமாகப்பிரி, அது OPயை வெட்டும் புள்ளி M.
4. M யை மையமாகவும், OM யை ஆரமாகவும் கொண்டு வட்டம் வரைக.
5. இரு வட்டங்களும் சந்திக்கும் புள்ளிகள்
6. AP, BP யை இணை