Samacheer Kalvi 10th Maths Guide Chapter 3 இயற்கணிதம் Unit Exercise 3

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 3 இயற்கணிதம் Unit Exercise 3 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 3 இயற்கணிதம் Unit Exercise 3

கேள்வி 1.
தீர்க்க : \(\frac { 1 }{ 3 }\)(x + y – 5) = y – z = 2x – 11 = 9 – (x + 2z)
தீர்வு:
\(\frac { 1 }{ 3 }\)(x+y-5) = y – z
x + y – 5 = 3(y – z)
x + y – 5 = 3y – 3z
x – 2y + 3z = 5——(1)
மற்றும் y – z = 2x – 11
2x – y + z = 11 —–(2)
மற்றும் 2x – 11 = 9 – (x + 2z)
2x – 11 = 9 – x -2z
3x + 2z = 20 ——(3)
(1) & (2) ஐ தீர்க்க

11y = 9
(3) & (4) ஐ கூட்ட

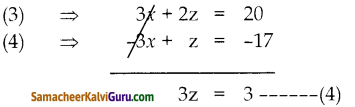
z = 1

z = 1 ஐ (3)ல் பிரதியிட
3x + 2 = 20
3x = 18
x = 6

x = 6, z = 1 ஐ (1) ல் பிரதியிட
6 – 2y + 3 = 5
9 – 2y = 5
9 – 5 = 2y
y = 2
∴ x = 6, y = 2, z = 1

கேள்வி 2.
ஒரு புள்ளியில் A, B மற்றும் C என்ற மூன்று பிரிவுகளில் 150 மாணவர்கள் புதிதாகச் சேர்க்கப்படுகின்றனர். பிரிவு C க்கு 6 மாணவர்கள் A யிலிருந்து பிரிவு மாற்றப்பட்டால் இரு பிரிவுகளிலும் சமமான மாணவர்கள் இருப்பர். C பிரிவு மாணவர்களின் எண்ணிக்கையின் 4 மடங்கு மற்றும் A பிரிவு மாணவர்களின் எண்ணிக்கை இவற்றின் வித்தியாசம் B பிரிவு மாணவர்களின் எண்ணிக்கைக்குச் சமம் எனில், மூன்று பிரிவுகளில் உள்ள மாணவர்களின் எண்ணிக்கையைக் காண்க.
தீர்வு :
பிரிவு A, B மற்றும் Cல் உள்ள மாணவர்களின் எண்ணிக்கையை x y மற்றும் z என்க
கணக்கின் படி x + y + z = 150 ——-(1)
x – 6 = z + 6 மற்றும் x – z = 12 ——-(2) மற்றும்
4z = x + y
x + y – 4z = 0 ——-(3)
(1) & (3) லிருந்து

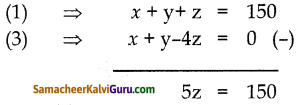
z = 30
z = 30 யை (2),ல் பிரதியிட
x – 30 = 12
x = 42
x = 42, Z = 30 யை (1),ல் பிரதியிட
42 + y + 30 = 150
y = 78
∴ A, B, C பிரிவிலுள்ள மாணவர்களின் எண்ணிக்கை 42, 78, 30.

கேள்வி 3.
ஒரு மூன்றிலக்க எண்ணின், பத்தாம் இட மற்றும் நூறாம் இட இலக்கங்களை இடமாற்றுவதன் மூலம் கிடைக்கும் புதிய எண், கொடுக்கப்பட்ட எண்ணின் மும்மடங்கைவிட 54 அதிகம். கொடுக்கப்பட்ட எண்ணோடு 198 ஐ கூட்டினால் இலக்கங்கள் இட வலப்பக்கமாக வரிசை மாறும். ஒன்றாம் இட இலக்கத்தைவிட அதிகமுள்ள பத்தாம் இட இலக்கத்தின் இரு மடங்கு , நுாறாம் இட இலக்கத்தை விட அதிகமுள்ள பத்தாம் இட இலக்கத்திற்குச் சமம் எனில், கொடுக்கப்பட்ட எண்ணைக் காண்க.
தீர்வு ;
மூவிலக்க எண்ணை xyz என்க. கணக்கின் படி,
yxz = 3xyz + 54
100y + 10x + z = 300x + 30y + 3z + 54
290x-70y+2z = -54
÷ by 2 ⇒ 145x – 35y + z = -27 ——(1) மற்றும்
xyz + 198 = zyx
100x + 10y + z + 198 = 100z + 10y + x
99x – 99z = -198
÷by 99 ⇒ x-z = -2 ——(2) மற்றும்
y = 2x + z
2x – y + z = 0——(3)
இப்பொழுது

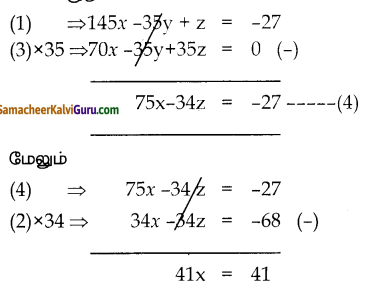
x = 1
x = 1 ஐ (2)ல் பிரதியிட
1 – z = – 2
z = 3
x = 1, z = 3 யை (3)ல் பிரதியிட
2 – y + 3 = 0
y = 5
∴ மூவிலக்க எண் 153.

கேள்வி 4.
xy(k² + 1) + k(x² + y²) மற்றும்
xy(k² – 1) + k(x² – y²) ஆகியவற்றின்
மீ.பொ.ம காண்க.
தீர்வு :
xy(k² + 1) + k(x² + y)) = k²xy + xy + kx² + ky²
= ky(kx + y) + x(kx + y)
(kx+y) (ky+x) —(1)
மற்றும்
xy(k² – 1) + k(x² – y²)) = k²xy – xy + kx² – ky²
= ky(kx – y) + x(kx – y) |
= (kx – y) (ky + x) —(2)
(1) & (2)ன் மீ.பொ.ம
(ky + x) (kx – y) (kx + y) = (ky+x) (k²x² – y²)

கேள்வி 5.
வகுத்தல் படிமுறையைப் பயன்படுத்தி 2x⁴ + 13x³ + 27x² + 23x + 7, x³ + 3x² + 3x + 1, x² + 2x + 1 ஆகியவற்றின் மீ.பொ.வ காண்க.
தீர்வு :
முதல் இரண்டு பல்லுறுப்புக்கோவையில் இருந்து

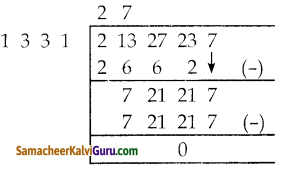
∴ முதல் இரண்டின் மீ.பொ.வ x³ + 3x² + 3x + 1
இப்பொழுது மூன்றாவது
பல்லுறுப்புக்கோவையின் மீ.பொ.வ

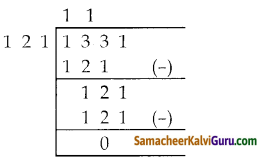
∴ கொடுக்கப்பட்ட பல்லுறுப்புக்கோவையின் மீ.பொ.வ x² + 2x + 1

கேள்வி 6.
பின்வரும் விகிதமுறு கோவைகளை எளிய வடிவில் சுருக்குக்
i) \(\frac{x^{3 a}-8}{x^{2 a}+2 x^{n}+4}\)
ii) \(\frac{10 x^{3}-25 x^{2}+4 x-10}{-4-10 x^{2}}\)
தீர்வு :

கேள்வி 7.
சுருக்குக :
\(\frac{\frac{1}{p}+\frac{1}{q+r}}{\frac{1}{p}-q+r} \times\left(1+\frac{q^{2}+r^{2}-p^{2}}{2 q r}\right)\)
தீர்வு:

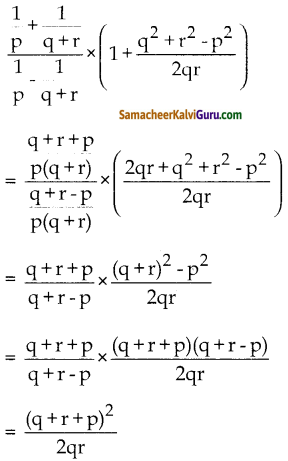
கேள்வி 8.
அருள், மதன் மற்றும் இராம் மூவரும் இணைந்து ஒரு கடையை 6 மணி நேரத்தில் சுத்தம் செய்கின்றனர். தனித்தனியாகச் சுத்தம் செய்தால் அருளைப் போல இருமடங்கு நேரம் மதன் எடுத்துக் கொள்கிறார். மேலும் இராம் அருளின் நேரத்தைப் போல மும்மடங்கு எடுத்துக்கொள்கிறார் எனில், மூவரும் தனித்தனியாக எவ்வளவு நேரம் எடுத்துக் கொள்வார்கள்?
தீர்வு :
அருள், மதன் மற்றும் இராம் மூவரும் தனித்தனியாக அவ்வேலையை செய்ய எடுத்துக்கொள்ளும் நேரத்தை x, y, z. என்க.
∴ 1 மணி நேரத்தில் இவர்கள் செய்யும் வேலையின் நேரம் \(\frac{1}{x}, \frac{1}{y}, \frac{1}{z}\) ஆகும்.
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{6}\) ——– (1)
\(\frac{2}{y}=\frac{1}{x}\) ——– (2)
\(\frac{3}{z}=\frac{1}{x}\) ——– (3)
\(\frac{1}{x}\) = a,
\(\frac{1}{x}\) = b,
\(\frac{1}{z}\) = c என்க
(1) ⇒ a + b + c = – ——(4)
(2) ⇒ a – 2b = 0 ——(5)
(3) ⇒ a – 3c = 0 ——(6)
இப்பொழுது

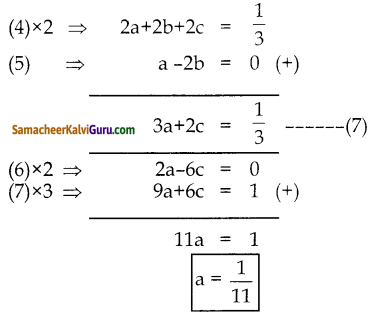
a = \(\frac{1}{11}\)ஐ (5) ல் பிரதியிட
\(\frac{1}{11}\) – 2b = 3
2b = \(\frac{1}{11}\)
b = \(\frac{1}{22}\)
a = \(\frac{1}{11}\) ஐ (6) ல் பிரதியிட
\(\frac{1}{11}\) – 3c = 0
3c = \(\frac{1}{11}\)
c = \(\frac{1}{33}\)
∴ x = 11 hrs.
y = 22 hrs.
z = 33 hrs.

கேள்வி 9.
289x⁴ – 612x³ + 970x² – 684x + 361 – யின் வர்க்கமூலம் காண்க.
தீர்வு :

∴ வர்க்கமூலம் = |17x² – 18x + 19|

கேள்வி 10.
தீர்க்க : \(\sqrt{y+1}+\sqrt{2 y-5}\) = 3
தீர்க்க :
இருபுறமும் வர்க்கம் காண

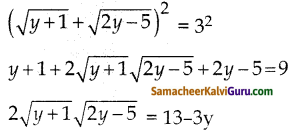
மீண்டும் இருபுறமும் வர்க்கம் காண
4(y + 1)(2y – 5) = (13 – 3y)
8y² – 12y – 20 = 169 – 78y + 9y²
y² – 66y + 189 = 0
(y – 3) (y – 63) = 0
∴ y = 3, 63

கேள்வி 11.
36கி.மீ தூரத்தை ஒரு படகு நீரோட்டத்தின் திசையில் கடக்கும் நேரத்தைவிட எதிர்திசையில் கடக்கும் நேரம் 1.6 மணி நேரம் அதிகமாக எடுத்துக்கொள்கிறது. நீரோட்டத்தின் வேகம் 4 கிமீ/மணி எனில், அசைவற்ற நீரில் படகின் வேகம் என்ன?
தீர்வு :
படகின் வேகம் x km/hr என்க
நீரோட்டத்தின் வேகம் 4 km/hr.
நீரோட்டத்தின் எதிர்திசையின் வேகம் (x – 4) km/ hr
∴ நீரோட்டத்தின் வேகம் (x + 4) km/ hr கணக்கின் படி
36 கி.மீ தூரத்தை ஒரு படகு நீரோட்டத்தின் திசையில் கடக்கும் நேரத்தை விட எதிர் திசையில் கடக்கும் நேரம் 1.6 மணி நேரம் அதிகமாக உள்ளது.

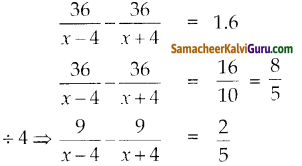
9(x + 4) – 9(x – 4) = \(\frac{2}{5}\)(x-4)(x+4) சுருக்க
x² – 16 = 180
x² = 196
x = 14
அசைவற்ற நீரில் படகின் வேகம் 14km/hr.

கேள்வி 12.
320 மீ சுற்றளவும் 4800 ச.மீ பரப்பளவும் கொண்ட செவ்வக வடிவப் பூங்காவை அமைக்க முடியுமா? ஆம் எனில், அதன் நீளம், அகலம் காண்க.
தீர்வு :
செவ்வக வடிவ பூங்காவின் நீளம் மற்றும் அகலத்தை l மற்றும் b என்க. கணக்கின் படி,
2(l + b) = 320 ——(1)
lb = 4800 —–(2)
(1)= 2 (\(l+\frac{4800}{l}\)) = 320
2(\(\frac{l^{2}+4800}{l}\)) = 320
2(l² + 4800) = 320l +2
÷2 ⇒ l² – 160l + 4800 = 0
(l – 120)(l – 40) = 0
∴ l = 120 (or) 40
l > b , l = 120மீ & 40மீ
11, 11, 22

கேள்வி 13.
ஒரு கடிகாரத்தில் பிற்பகல் 2 மணியிலிருந்து t நிமிடங்களுக்குப் பிறகு 3 மணியை அடைவதற்குரிய கால அளவானது \(\frac{t^{2}}{4}\)ஐ விட மூன்று நிமிடங்கள் குறைவு எனில், யின் மதிப்பைக் காண்க
தீர்வு :
கடிகாரத்தில் பிற்பகல் 2 மணியிலிருந்து t நிமிடங்களுக்குப் பிறகு 3 மணியை அடைவதற்குரிய கால அளவு (60 – t) வினாடி 60 – t = \(\frac{t^{2}}{4}\) – 3
\(\frac{t^{4}}{4}\) = 63 – t
t² = 252-4t
t² + 4t – 252 = 0
(t + 18) (t – 14) = 0
t = 14, -18
t = -18 இருக்க இயலாது
∴ t = 14 நிமிடம்.

கேள்வி 14.
ஓர் அரங்கில், ஒரு வரிசையில் உள்ள இருக்கைகளின் எண்ணிக்கை அந்த அரங்கில் உள்ள மொத்த வரிசைகளின் எண்ணிக்கைக்குச் சமம். ஒவ்வொரு வரிசையில் உள்ள இருக்கைகளை 5 குறைத்து மொத்த வரிசைகளின் எண்ணிக்கை இரட்டிப்பாக்கிளால் அரங்கில் உள்ள இருக்கைகளின் எண்ணிக்கையை இரட்டிப்பாக்கினால் அரங்கில் உள்ள இருக்கைகளின் எண்ணிக்கை முன்பைவிட 375 அதிகரிக்கும். அரங்கில் துவக்கத்தில் இருந்த வரிசைகளின் எண்ணிக்கையைக் காண்க.
தீர்வு :
அரங்கில் துவக்கத்தில் இருந்த வரிசைகளின் எண்ணிக்கை x என்க.
கணக்கின் படி,
ஒரு வரிசையில் உள்ள இருக்கைகளின் எண்ணிக்கை அந்த அரங்கில் உள்ள மொத்த வரிசைகளின் எண்ணிக்கைக்குச் சமம்.. மொத்த இருக்கைகளின் எண்ணிக்கை = x²
கொடுக்கப்பட்ட விபரங்களின் படி
x² + 375 = 2x(x-5)
x² + 375 = 2x² – 10x
x² – 10x – 375 = 0
(x – 25)(x + 15) = 0
x = 25, -15
x குறை எண் அல்ல x = 25
∴ வரிசைகளின் எண்ணிக்கை 25

கேள்வி 15.
f(x) = x² – 2x + 3, என்ற பல்லுறுப்புக் கோவையின் மூலங்கள் α மற்றும் β எனில், கீழ்க்கண்டவற்றை மூலங்களாகக் கொண்ட பல்லுறுப்புக் கோவையைக் காண்க.
(i) α + 2, β + 2
(ii) \(\frac{\alpha-1}{\alpha+1}, \frac{\beta-1}{\beta+1}\)
தீர்வு :
αβ என்பன x²-2x+3 ன் மூலங்கள்
α + β = +2 & αβ = 3
i) புதிய மூலங்க ள் (α+2, β+2)
மூலங்களின் கூடுதல் = α+2+β+2
= α+β+4
= +2+4
= 6
மூலங்களின் பெருக்கல் = (α+2) (β+2)
= αβ + 2(α + β)+ 4
= 3 + 2( + 2) + 4
= 3 + 4 + 4
= 11

பல்லுறுப்புக்கோவை
⇒ x² – (மூ.கூ)x + மூ.பெ
= x² – 6x + 11

பல்லுறுப்புக்கோவை
x² -( மூ.கூ)x+ மூ.பெ
⇒ x² – \(\frac{2}{3} x+\frac{1}{3}\)

கேள்வி 16.
x² + px – 4 = 0 என்ற சமன்பாட்டின் மூலம் – 4 மற்றும் x² + px + 4 = 0 யின் மூலங்கள் சமம் எனில், p மற்றும் 4 யின் மதிப்புக் காண்க.
தீர்வு :
-4 என்பது x² + px – 4 = 0 ன் ஒருமூலம்
x = -4, ஐ பிரதியிட
(-4)² + p(-4) – 4 = 0
16 – 4p – 4 = 0
12 = 4p
p = 3
மேலும் கணக்கின் படி x² + px + q = 0 ன் மூலங்கள் சமம்.
⇒ x² + 3x + q = 0
சம மூலங்களை α,α என்க
α + α = -3
2α = -3
α = \(\frac{-3}{2}\)
α² = q
\(\) = q

கேள்வி 17.
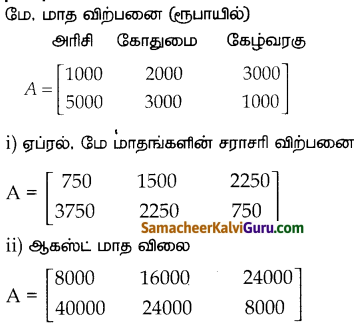
திலகன், கௌசிகன் என்ற இரு விவசாயிகள் அரிசி, கோதுமை மற்றும் கேழ்வரகு ஆகிய மூன்று தானியங்களைப் பயிரிட்டனர். ஏப்ரல் மாதத்தில் இருவருக்குமான தானியங்களின் விற்பனை விலை கீழ்க்கண்ட அணியில் கொடுக்கப்பட்டுள்ளது.
ஏப்ரல், மாத விற்பனை (ரூபாயில்)

மேலும் மே மாத விலை ஏப்ரல் மாத கௌசிகன் விலையின் இருமடங்கு எனில், கீழ்க்கண்டவற்றை காண்க.
i) ஏப்ரல், மே மாதங்களின் சராசரி விற்பனை யாது?
ii)இதே போல் விலை தொடர்ந்து வரும் மாதங்களில் ஏற்றமடைந்தால் ஆகஸ்ட் மாத விலையைக் காண்க.
தீர்வு :
மே, மாத விற்பனை (ரூபாயில்)

கேள்வி 18.
\(\cos \theta\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]+\sin \theta\left[\begin{array}{cc}
x & -\cos \theta \\
\cos \theta & x
\end{array}\right]=\mathrm{I}_{2}\)
எனில் x -ஐக் காண்க.
தீர்வு :

x sin θ + cos² θ
x sin θ = 1 – cos²θ
= sin²θ
∴ x = \(\frac{\sin ^{2} \theta}{\sin \theta}\)
x = sin θ

கேள்வி 19.
A = \(\left[\begin{array}{ll}
p & 0 \\
0 & 2
\end{array}\right]\)
B = \(\left[\begin{array}{cc}
0 & -\mathrm{q} \\
1 & 0
\end{array}\right]\)
C = \(\left[\begin{array}{cc}
2 & -2 \\
2 & 2
\end{array}\right]\)
மற்றும் BA = C² எனில் யைக் காண்க.
தீர்வு :

கணிதம் கணக்கின் படி BA = C²
\(\left[\begin{array}{cc}
0 & -2 q \\
p & 0
\end{array}\right]=\left[\begin{array}{cc}
0 & -8 \\
8 & 0
\end{array}\right]\)
∴ p = 8, -2q = -8 ⇒ q = 4

(31+6c 3b+6d) [18 9) [0 -2q] = [0 -8
b+d | 64 37 p (0) – (80)
3a+6c = 18

3(a+2c) = 18
a+2c = 6——(1)
a+c = 64—–(2)

கேள்வி 20.
A = \(\left[\begin{array}{ll}
3 & 0 \\
4 & 5
\end{array}\right]\) B = \(\left[\begin{array}{ll}
6 & 3 \\
8 & 5
\end{array}\right]\) C = \(\left[\begin{array}{ll}
3 & 6 \\
1 & 1
\end{array}\right]\) எனில் CD-AB = 0 எனுமாறு அணி D ஐக் காண்க.
தீர்வு :

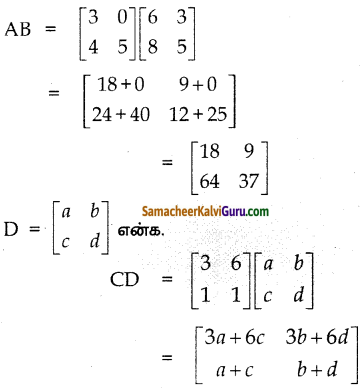
கணக்கின் படி
CD – AB = 0
CD = AB
\(\left[\begin{array}{cc}
3 a+6 c & 3 b+6 d \\
a+c & b+d
\end{array}\right]=\left[\begin{array}{cc}
18 & 9 \\
64 & 37
\end{array}\right]\)
3a + 6c = 18
3(a + 2c) = 18
a + 2c = 6-(1)
a + c = 64 (2)
3b + 6d = 9
b + 2d = 3 ——(3)
b + d = 37 —–(4)

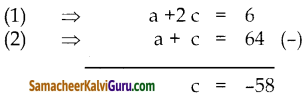
c = -58 ஐ (2),ல் பிரதியிட
a + c = 64
a – 58 = 64
a = 64 + 58
a= 122

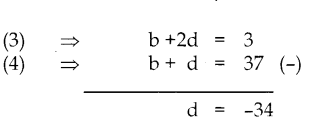
d = -34 ஐ (4)ல் பிரதியிட b = 71 கிடைக்கும்
D = \(\left[\begin{array}{cc}
122 & 71 \\
-58 & -34
\end{array}\right]\)