Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.1 Textbook Questions and Answers, Notes.
TN Board 10th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.1
![]()
கேள்வி 1.
கீழ்க்காணும் மூன்று மாறிகளில் அமைந்த ஒருங்கமை நேரியல் சமன்பாட்டுத் தொகுப்புகளைத் தீர்க்க .
i) x + y + z = 5, 2x – y + z = 9; x – 2y + 3z = 16
ii) \(\frac{1}{x}-\frac{2}{y}+4=0 ; \frac{1}{y}-\frac{1}{z}+1=0, \frac{2}{z}+\frac{3}{x}=14\)
iii) x + 20 = \(\frac{3 y}{2}\) + 10 = 2z + 5 = 110 – (y + z )
தீர்வு :
x+y + z = 5 — (1)
2x – y + z = 9 — (2)
x – 2y + 3z = 16 — (3)
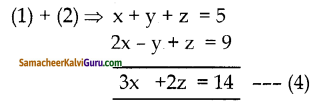
(1) x (2) ⇒ 2x + 2y + 2z = 10
(3) x- 2y + 3z = 16
3x + 5z = 26 —— (5)
(5) – (4) 3x + 5z = 26
3x + 2z = 14 (-)
3z = 12
z = 4
z = 4 ஜ (4) ல் பிரதியிட
3x + 2 × 4 = 14
3x + 8 = 14
3x = 14 – 8 = 16
x = 2
![]()
x = 2, z = 4 ஐ (1) ல் பிரதியிட
2 + y + 4 = 5
6+ y = 5
y = 5 – 6
y = -1
∴ x = 2, y = -1, z = 4
ii) \(\frac{1}{x}\) = a, \(\frac{1}{y}\) = b, \(\frac{1}{z}\) = c என்க
\(\frac{1}{x}-\frac{2}{y}\) + 4 = 0 = a – 2b + 4 = 0 — (1)
\(\frac{1}{y}-\frac{1}{z}\) + 1 = 0 = b – c + 1 = 0 — (2)
\(\frac{2}{z}+\frac{3}{x}\)= 14 = 2c + 3a – 14 = 0 — (3)
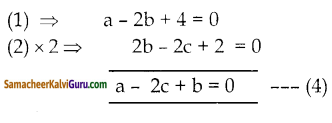
a = 2 ஐ (1)ல் பிரதியிட
2 – 2b + 4 = 0
2b = 6
b = 3
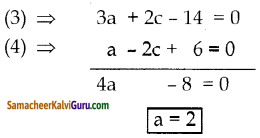
b = 3 ஐ (2)ல் பிரதியிட
3 – c + 1 = 0
c = 4
∴ \(x=\frac{1}{a}=\frac{1}{2}, y=\frac{1}{b}=\frac{1}{3}, z=\frac{1}{c}=\frac{1}{4}\)
iii) x + 20 = \(\frac{3 y}{2}\) + 10 எனில்
⇒ x + 20 – 10 = \(\frac{3 y}{2}\)
⇒ x + 10 = \(\frac{3 y}{2}\)
⇒ 2(x + 10) = 3y
⇒ 2x + 20 – 3y = 0
⇒ 2x – 3y + 20 = 0 — (1)
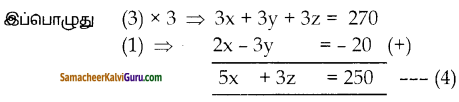
x + 20 = 2z + 5 எனில்
⇒ x – 2z + 20 – 5 = 0
⇒ x – 2z + 15 = 0 —– (2)
x + 20 = 110 – (y + z) எனில்
x + y + z = 90 — (3)
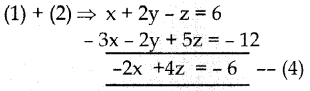

z = 25 ஐ (2)ல் பிரதியிட
x – 2 × 25 + 15 = 0
x – 50 + 15 =0
x – 35 = 0
x = 35
x = 35, z = 25 ஐ (3) ல் பிரதியிட
35 + y + 25 = 90
60 + y = 90
y = 90 – 60
y = 30
∴ x = 35, y = 30, Z = 25
![]()
கேள்வி 2.
கீழ்க்காணும் சமன்பாட்டுத் தொகுப்புகளின் தீர்வுகளின் தன்மையைக் காண்க.
i) x + 2y – z = 6; – 3x – 2y + 5z = -12; x – 2z = 3
ii) 2y + z = 3 (-x + 1); – x + 3y – z = -4; 3x + 2y + z = \(-\frac { 1 }{ 2 }\)\
iii) \(\frac{y+z}{4}=\frac{z+x}{3}=\frac{x+y}{2}\), x + y + z = 27
தீர்வு :
i) x + 2y = z = 6 —(1)
– 3x – 2y + 5z = -12 — (2)
x – 27 = 3 — (3)
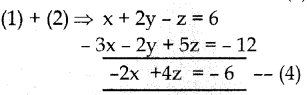
(4) ⇒ – 2x + 4z = – 6
(3) × 2 ⇒ 2x – 4z = 6 (+)
0 = 0
கொடுக்கப்ட்ட சமன்பாட்டு தொகுப்பிற்கு எண்ணற்ற தீர்வுகள் உண்டு
ii) 2y + z = 3 (- x + 1)
⇒ 2y + z = -3x +3
⇒ 3x + 2y + z = 3 — (1)
– x +3y – z = 4 — (2)
3x + 2y + z = \(-\frac{1}{2}\) —–(3)
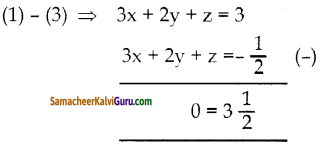
இத்தொகுப்பானது ஒருங்கமைவற்றது மேலும் இச்சமன்பாடுக்கு தீர்வு இல்லை
iii) x + y + z = 27 – —(1)
\(\frac{y+z}{4}=\frac{z+x}{3}\)என்க
3y + 3z = 4z + 4x
4x – 3y + z = 0 — (2)
\(\frac{y+z}{4}=\frac{x+y}{2}\) என்க
⇒ 2y + 2z = 4x + 4y
⇒ 4x + 2y – 2z = 0 — (3)
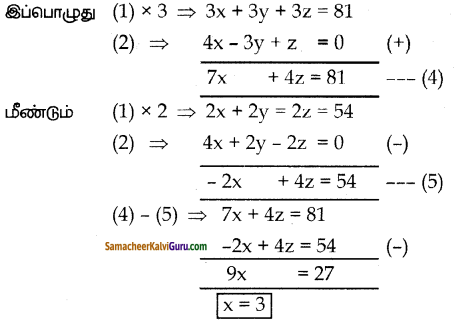
இச்சமன்பாடுக்கு ஒரேயொரு தீர்வு உண்டு
![]()
கேள்வி 3.
தாத்தா , தந்தை மற்றும் வாணி ஆகிய மூவரின் சராசரி வயது 53. தாத்தாவின் வயதில் பாதி, தந்தையின் வயதில் மூன்றில் ஒரு பங்கு மற்றும் வாணியின் வயதில் நான்கில் ஒரு பங்கு ஆகியவற்றின் கூடுதல் 65. நான்கு ஆண்டுகளுக்கு முன் தாத்தாவின் வயது வாணியின் வயதைப்போல் நான்கு மடங்கு எனில் மூவரின் தற்போதைய வயதைக் காண்க?
தீர்வு :
வாணி , வாணியின் தந்தை மற்றும் வாணியின் தாத்தா ஆகியோரின் தற்போதைய வயதுகள் முறையே x, y, z என்க.
கொடுக்கப்பட்ட விபரங்களின் படி
\(\frac{x+y+z}{3}\)= 53
⇒ x + y + z = 159 —— (1)
⇒ \(\frac{x}{4}+\frac{y}{3}+\frac{z}{2}\) = 65
⇒ \(\frac{3 x+4 y+6 z}{12}\) = 65
⇒ 3x + 4y + 6z = 780 —(2)
நான்கு ஆண்டுகளுக்கு முன்
z – 4 = 4(x – 4)
⇒ 4x – z = 12 —— (3)
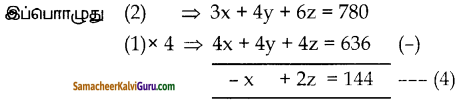
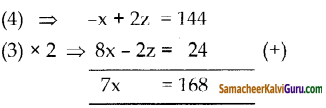
x = 24
x = 24 ஐ சமன்பாடு (3)
பிரதியிட
4 × 24 – z = 12
96 – a = 12
z = 84
x = 24, z = 84 ஐ (1)ல்
பிரதியிட
24 + y + 84 = 159
y = 51
∴ வாணியின் வயது 24
வாணியின் தந்தையின் வயது 51
வாணியின் தாத்தாவின் வயது 84
![]()
கேள்வி 4.
ஒரு மூவிலக்க எண்ணில், இலக்கங்களின் கூடுதல் 11. இலக்கங்களை இடமிருந்து வலமாக வரிசை மாற்றினால் புதிய எண் பழைய எண்ணின் ஐந்து மடங்கைவிட 46 அதிகம். பத்தாம் இட இலக்கத்தின் இரு மடங்கோடு நூறாம் இட இலக்கத்தைக் கூட்டினால் ஒன்றாம் இட இலக்கம் கிடைக்கும் எனில், அந்த மூவிலக்க எண்ணைக் காண்க?
தீர்வு :
அந்த மூவிலக்க எண் xyz என்க
கணக்கின் படி, இலக்கங்களின் கூடுதல் = 11
∴ x + y + z = 11 — (1)
இலக்கங்களை இடமிருந்து வலமாக வரிசை மாற்றினால் புதிய எண் பழைய எண்ணிண் ஐந்து மடங்கை விடை 46 அதிகம், zyx = 5xyz + 46
⇒ 100z + 10y + x = 500x + 50y + 5z + 46
⇒ 499x + 40y – 95z = – 46 — (2)
கணிதம் கணக்கின் படி, x + 2y = z
⇒ x + 2y – z = 0 — (3)
(1) & (3) ஐ கூட்ட
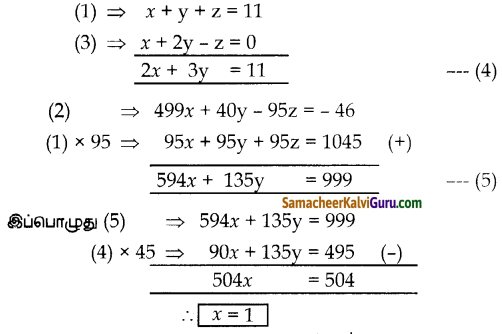
x = 1 ஐ (4) ல் பிரதியிட
2 × 1 + 3y = 11
3y = 9
y = 3
x = 1, y = 3 ஐ (1) ல் பிரதியிட
1 + 3 + z = 11
z = 7
∴ அந்த மூவிலக்க எண் 137
![]()
கேள்வி 5.
ஐந்து, பத்து மற்றும் இருபது ரூபாய் நோட்டுகளின் மொத்த மதிப்பு ₹105 மற்றும் மொத்த நோட்டுகளின் எண்ணிக்கை 12. முதல் இரண்டு வகை நோட்டுகளின் எண்ணிக்கையை இடமாற்றம் செய்தால் முந்தைய மதிப்பை விட ₹ 20 அதிகரிக்கிறது எனில், எத்தனை ஐந்து, பத்து மற்றும் இருபது ரூபாய் நோட்டுகள் உள்ளன? தீர்வு :
ஐந்து, பத்து மற்றும் இருபது ரூபாய் நோட்டுகளின் எண்ணிக்கையை முறையே x, y, z என்க. கணக்கின் படி x + y + z = 12 — (1)
5x + 10y + 20z = 105
⇒ x + 2y +4z = 21 — (2)
முதல் இரண்டு வகை நோட்டுகளின் எண்ணிக்கையை இடமாற்றம் செய்தால் முந்தைய மதிப்பை விட ₹20 அதிகரிக்கிறது
10x + 5y + 20z = 125
2x + y + 4z = 25 — (3)
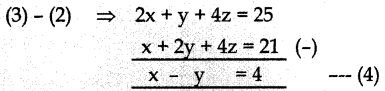

x = 7 ஐ (4) ல் பிரதியிட
7 – y = 4
∴ y = 3
x = 7, y = 3 ஐ (1) ல் பிரதியிட
7 + 3 + z = 12
∴ z = 2
∴ ஜந்து, பத்து மற்றும் இருபது ரூபாய் நோட்டுகளின் எண்ணிக்கை 7, 3, 2 ஆகும்.