Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.8 Textbook Questions and Answers, Notes.
TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.8
![]()
கேள்வி 1.
பெருக்குத் தொடர்வரிசையில் முதல் n உறுப்புகளின் கூடுதல் காண்க.
(i) 5,-3, \(\frac{9}{5},-\frac{27}{25}\) ….
(ii) 256,64, 16,…
தீர்வு :
(i) 5,-3, \(\frac{9}{5},-\frac{27}{25}\) ….
தரவு: 5, -3 \(\frac{9}{5},-\frac{27}{25}\) …. என்பவை பெருக்குத் தொடர்வரிசை

ii) 256, 64, 16 …
தீர்வு :

கேள்வி 2.
5, 15, 45, ….. என்ற பெருக்குத்
தொடர்வரிசையின் முதல் 6 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு :
தரவு : a = 5, r = 15/3 = 3 > 1, n = 6

![]()
கேள்வி 3.
ஒரு பெருக்குத் தொடர்வரிசையின் பொது விகிதம் 5 மற்றும் முதல் 6 உறுப்புகளின் கூடுதல் 46872 எனில், அதன் முதல் உறுப்பைக் காண்க.
தீர்வு :
தரவு : r = 5, S6 = 46872 எனில்
a = ?
Sn = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
46872 = \(\frac{a\left[5^{6}-1\right]}{5-1}\)
46872 = \(\frac{a[15625-1]}{4}\)
46872 = a x \(\frac{15624}{4}\)
46872 = 39069
a = \(\frac{46872}{3906}\)
a = 12
கேள்வி 4.
பின்வரும் முடிவுறா தொடர்களின் கூடுதல் காண்க.
(i) 9 + 3 +1+…..
(ii) 21+14+ 28…………..
தீர்வு:
i) 9+3+1+…………….

ii) 21 + 14 + \(\frac{28}{3}\) + …………
தரவு a = 9, r = \(\frac{14}{21}=\frac{2}{3}\) < 1
Sr = \(\frac{a}{1-r}\)
= \(\frac{21}{1-\frac{2}{3}}\)
= \(\frac{21}{\frac{1}{3}}\)
= 21 x \(\frac{3}{1}\)
S∞ = 63
கேள்வி 5.
ஒரு முடிவுறா பெருக்குத் தொடரின் முதல் உறுப்பு 8 மற்றும் முடிவுறா உறுப்புகள் வரை கூடுதல் \(\frac { 32 }{ 3 }\) எனில் அதன் பொது விகிதம் காண்க.
தீர்வு :
தரவு : a = 8, S∞ = \(\frac { 32 }{ 3 }\)
r = ?
S∞ = \(\frac{a}{1-r}\)
\(\frac{32}{3}=\frac{8}{1-r}\)
32(1-r) = 24
32-32r = 24
32r = 32-24
32r = 8
r = \(\frac { 8 }{ 32 }\)
r = \(\frac { 1 }{ 4 }\)
![]()
கேள்வி 6.
பின்வரும் தொடர்களின் n உறுப்புகள் வரை கூடுதல் காண்க.
(i) 0.4 +0.44 +0.444 + ……….. n உறுப்புகள்
வரை (ii) 3 + 33 + 333 +………. n உறுப்புகள் வரை
தீர்வு :
i) 0.4 + 0.44 + 0.444 +. .. n உறுப்புகள் வரை
தரவு : 0.4 + 0.44 + 0.444 +….. n உறுப்புகள் வரை
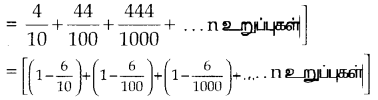
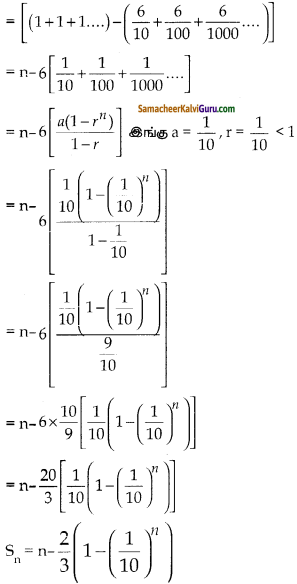
ii) 3 + 33 + 333 +…. n உறுப்புகள் வரை
தரவு :
3 + 33 + 333 +…. n உறுப்புகள் வரை
= 3[1 + 11 + 111 + n உறுப்புகள் வரை)
= \(\frac { 3 }{ 9 }\)[9+99+999+…. n உறுப்புகள்]
= \(\frac { 1 }{ 3 }\)[(10-1)+(100-1)+(1000-1)….nஉறுப்புகள்]
= \(\frac { 1 }{ 3 }\)[(10 + 100+1000+ …)-(1+1+1+ – n உறுப்புகள்)]
= \(\frac{1}{3}\left[\frac{a\left(r^{n}-1\right)}{r-1}-n\right]\)
இங்கே a = 10, r = 10 > 1

கேள்வி 7.
3 + 6 +12 +…..+ 1536 என்ற பெருக்குத் தொடரின் கூடுதல் காண்க.
தீர்வு :
தரவு:- a = 3, r = \(\frac { 6 }{ 3 }\) = 2 > 1
tn = 1536
arn-1 = 1536
3(2)n-1 = 1536
2n-1 = 1536/3
2n-1 = 512
2n-1 = 29
n-1 = 9
n = 9 + 1
n = 10
S10 = \(\frac{a\left(r^{n}-1\right)}{r-1}\) இங்கே a = 3, r = 2
= \(\frac{3\left[2^{10}-1\right]}{2-1}\)
= 3[1024-1]
= 3 x 1023
S10 = 3069
![]()
கேள்வி 8.
குமார் தனது நான்கு நண்பர்களுக்கு கடிதம் எழுதுகிறார். மேலும் தனது நண்பர்களை அவர்கள் ஒவ்வொருவரும் நான்கு வெவ்வேறு நண்பர்களுக்குக் கடிதம் எழுதுமாறும் மற்றும் இந்தச் செயல்முறையைத் தொடருமாறும் கூறுகிறார். இந்தச் செயல்முறை தொடர்ச்சியாக நடைபெறுகின்றது. ஒரு கடிதத்தற்கான செலவு ₹2 எனில் 8 நிலைகள் வரை கடிதங்கள் அனுப்புவதற்கு ஆகும் மொத்தச் செலவைக் காண்க.
தீர்வு :
4 + 16 + 64 + …… 8 நண்ப ர்கள்
a = 4, r = \(\frac { 16 }{ 4 }\) = 4> 1, n = 8
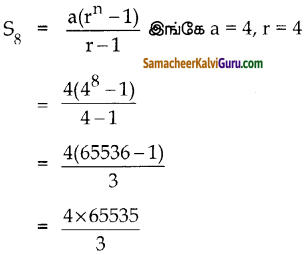
= 87380 கடிதங்கள்.
ஒரு கடிதத்திற்கான செலவு = ₹2
87380 கடிதங்களுக்கான செலவு = 87380 x 2
=₹174760
கேள்வி 9.
\(0 . \overline{123}\) என்ற எண்ணின் விகிதமுறு வடிவம் காண்க.
தீர்வு :
\(0 . \overline{123}\) = 0.123123123………
= 0.123 + 0.000123 + 0.000000123….
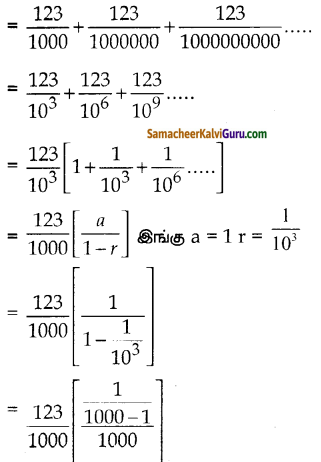
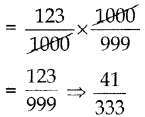
![]()
கேள்வி 10.
Sn = (x+y) + (x2 + xy + y2) +
(x3 + x2y + xy2 + y3)+ …….. n உறுப்புகள் வரை எனில் (x-y)Sn
= \(\left[\frac{x^{2}\left(x^{n}-1\right)}{x-1}-\frac{y^{2}\left(y^{n}-1\right)}{y-1}\right]\) என நிறுவுக.
தரவு:
Sn = (x+y) + (x2+xy+y2)
+(x3+x2y+xy2 +y3)+ ………….n
உறுப்புகள்
(x-y)Sn = (x-y) [ (x+y) + (x2 +xy+y2) + (x3+x2y +xy2 + y3)+…..n உறுப்புகள்]
= (x-y)(x+y)+(x-y)(x2+xy+y2)+(x-y) –
(x3+x2y+xy2+y3)+ ……n உறுப்புகள் =x2-y2 +x3-y3+ x4-y4+ ………… n உறுப்புகள்
= (x2+x3+x4 +…….. )-(y2 + y3 + y4+………………… )
a = x2 , r = \(\frac{x^{3}}{x^{2}}\) = x, a = y2, r = \(\frac{y^{3}}{y^{2}}\) = y
(x – y)Sn = \(\left[\frac{x^{2}\left(x^{n}-1\right)}{x-1}-\frac{y^{2}\left(y^{n}-1\right)}{y-1}\right]\)