Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.5 Textbook Questions and Answers, Notes.
TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.5
![]()
கேள்வி 1.
பின்வரும் தொடர் வரிசைகள் ஒரு கூட்டுத் தொடர்வரிசையா எனச் சோதிக்கவும்.
(i) a-3, 4-5, a-7,…
(ii) \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots\)
(iii) 9, 13, 17, 21, 25,…..
(iv) \(\frac{-1}{3}, 0, \frac{1}{3}, \frac{2}{3}, \ldots\)
(v) 1, -1, 1-1,1,-…
தீர்வு :
i) a-3, a-5, a-7
t2 – t1 = (a – 5) – (a – 3) = a – 5 – a + 3 = -2
t3 – t2 = (a – 7) – (a – 5) = a – 7 – a + 5 = -2
t2 – t1 = t3 – t2
பொது வித்தியாசங்கள் சமம்.
எனவே a-3, a-5, a-7…. என்பது ஒரு கூட்டுத் தொடர்வரிசை A.P.
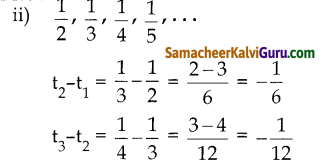
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம் இல்லை
இல்லை \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}\),… என்பது கூட்டுத்தொடர் 2 3 4 5 வரிசை அல்ல.
iii) 9, 13, 17, 21, 25…
t2 – t1 = 13-9 = 4
t3 – t2 = 17-13 = 4
t3 – t2 = t2 – t1
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்
எனவே 9, 13, 17, 21, 25…. என்பது கூட்டுத் தொடர் வரிசை.
iv) \(\frac{-1}{3}, 0, \frac{1}{3}, \frac{2}{3}, \ldots\)
t2 – t1 = 0 – \(\left(-\frac{1}{3}\right)=\frac{1}{3}\)
t3 – t2 = \(\frac{1}{3}-0=\frac{1}{3}\)
t2 – t1 = t3 – t2
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்.
எனவே \(\frac{-1}{3}, 0, \frac{1}{3}, \frac{2}{3}\) என்பது கூட்டுத் தொடர் வரிசை.
![]()
v) 1, -1, 1, -1, 1, -1…
t2 – t1 = -1-1 = -2
t3 – t2 = 1-(-1) = 1+1 = 2
t2 – t1 ≠ t3 – t2
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம் அல்ல.
எனவே 1,-1,1,-1,1,-1……… என்ப து கூட்டுத் தொடர் வரிசை அல்ல.
கேள்வி 2.
கீழே கொடுக்கப்பட்டுள்ள முதல் உறுப்பு a மற்றும் பொது வித்தியாசம் d-க்குக் கூட்டுத் தொடர்வரிசைகளைக் காண்க.
(i) a = 5, d = 6
(ii) a =7, d=-5
(iii) a = \(\frac { 3 }{ 4 }\), d = \(\frac { 1 }{ 2 }\)
தீர்வு:
i) a = 5, d = 6
கூட்டுத் தொடர் வரிசை a, a+d, a+2d,… 5, 5+6, 5+2(6), 5+3(6)+….. கூட்டுத் தொடர் வரிசை = 5, 11, 17, 23….. a =
ii) a = 7, d = -5
கூட்டுத் தொடர் வரிசை = 7, 7+(-5), 7+2(5), 7+3(-5), …
கூட்டுத் தொடர் வரிசை = 7, 7-5, 7-10, 7-15,….
கூட்டுத் தொடர் = 7, 2, -3, -8…..
iii) a = \(\frac { 3 }{ 4 }\) d = \(\frac { 1 }{ 2 }\)
கூட்டுத் தொடர் வரிசை = \(\frac{3}{4}, \frac{3}{4}+\frac{1}{2}\frac{3}{4}+2\left(\frac{1}{2}\right)+\ldots\)
கூட்டுத் தொடர் வரிசை = \(\frac{3}{4}, \frac{5}{4}, \frac{7}{4} \ldots\)
கேள்வி 3.
கீழே கொடுக்கப்பட்டுள்ள பொது
உறுப்புகளையுடைய கூட்டுத்
தொடர்வரிசைகளின் முதல் உறுப்பு மற்றும்
பொது வித்தியாசம் காண்க.
(i) tn = -3 + 2n
(ii) t1 = 4-7n
தீர்வு :
i) tn =-3+2n
t1 = -3+2(1) = -3+2 = -1
t2 = -3+2(2) = -3+4 = 1
எனவே d = t2 – t1 = 1-(-1) = 2
எனவே a = -1, d = 2
ii) tn = 4-7n
t1 = 4-7(1) = 4-7 = -3
t2 = 4-7(2) = 4-14 = -10
எனவே d = t2 – t1 = -10-(-3) = -10+3 = -7
ஆகையால் a = -3, d = -7
![]()
கேள்வி 4.
-11, -15, -19, …… என்ற கூட்டுத் தொடர்வரிசையின் 19-வது உறுப்பைக் காண்க .
தீர்வு :
-11, -15,-19… என்பது A.P
இங்கே a = -11,
d = t2 – t1 = -15-(-11) = -15+11 = -4
tn = a+(n-1)d
t19 = -11+(19-1)(-4)
= -11+(183-4)
= -11-72
= -83
கூட்டுத் தொடர்வரிசையில் 19வது உறுப்பு =-83.
கேள்வி 5.
16, 11,6, 1,… என்ற கூட்டுத்தொடர்வரிசையில் -54 என்பது எத்தனையாவது உறுப்பு?
தீர்வு :
கூட்டுத்தொடர் வரிசை = 16, 11,6,….-54
இங்கே a = 16, d = -5
tn = -54 என்க
= a + (n – 1) d =-54
16 + (n – 1)(-5) = -54
21-5n = -54|
-5n = -54-21
-5n = -75
5n = 75
n = 75/5
n = 15
15வது உறுப்பு = -54 ஆகும்.
கேள்வி 6.
9, 15, 21, 27 …… 183 என்ற கூட்டுத் தொடர்வரிசையின் நடு உறுப்புகளைக் காண்க.
தீர்வு:
கூட்டுத்தொடர் வரிசை = 9, 15, 21, 27, …., 183
இங்கே a = 9, d = 15-9 = 6
tn = a + (n – 1)d = 183
9+(n-1)6 = 183
9+6n-6 = 183
3+6n = 183
6n = 183 – 3
6n = 180
n = 180/6
n = 30
உறுப்புகளின் எண்ணிக்கை = 30
எனவே நடு உறுப்புகள் = t15 மற்றும் t16
t15 = 9+(15-1)6 = 9+(14×6) = 9+84 = 93
t16 = 9+(16-1)6 = 9+(15×6) = 9+900 = 99
எனவே நடு உறுப்புகள் = 93, 99.
![]()
கேள்வி 7.
ஒரு கூட்டுத் தொடர்வரிசையின் ஒன்பதாவது உறுப்பின் ஒன்பது மடங்கும், பதினைந்தாவது உறுப்பின் பதினைந்து மடங்கும் சமம் எனில் இருபத்து நான்காவது உறுப்பின் ஆறு மடங்கானது பூச்சியம் என நிறுவுக.
தீர்வு:
தரவு :- 9t9 = 15t15
நிரூபி :- 6t24 = 0
9t9 = 15t15
9(a+(9-1)d) = 15(a+(15-1)d)
9(a+8d) = 15(a+14d)
9a+72d = 15a+210d
5a+210d-9a-72d = 0
6a+138d = 0
6(a+23d) = 0
6(a+(24-1)d) = 0
எனவே 6t24 = 0
கேள்வி 8.
3 +k, 18 -k, 5k +1 என்பவை ஒரு கூட்டுத் தொடர்வரிசையில் உள்ளன எனில், k-யின் மதிப்புக் காண்க.
தீர்வு:
தரவு:- 3+k, 18-k, 5k+1 என்பவை ஒரு கூட்டுத்தொடர்வரிசை.
எனவே அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்.
t2 – t1 = 18-k-(3+k) = 18-k-3-k = 15-2k
t3 – t2 = 5k+1-(18-k) = 5k+1-18+k = 6k-17
6k-17 = 15-2k
6k+2k = 15+17
8k = 32
k = \(\frac{32}{8}\)
k = 4
கேள்வி 9.
x, 10, y, 24, z என்பவை ஒரு கூட்டுத் தொடர்வரிசையில் உள்ளன எனில், x, y, z ஆகியவற்றின் மதிப்பு காண்க. தீர்வு:\
x, 10, y, 24, z என்பவை ஒரு கூட்டுத் தொடர் வரிசை அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்.
t2 – t1 = 10
t3 – t2 = y-10
t4 – t3 = 24-y
t5 – t4 = z-24
t3 – t2 = t4 – t3
y – 10 = 24 – y
y + y = 24 + 10
2y = 34
y = 34/2
y = 17
t2 – t1 = t3 – t2 எனில்
10-x = y-10
10-x = 17-10 ( y = 17)
10-x = 7
-x = 7-10
-x = -3
x= 3
t4 – t3 = t5 – t4 எனில்
24 – y = z – 24
24 – 17 = z – 24
7 = z – 24
z = 7 + 24
x = 31
ஆகையால் . = 3, v = 17, 7 = 31
![]()
கேள்வி 10.
ஒரு சினிமா அரங்கின் முதல் வரிசையில் 20 இருக்கைகளும் மொத்தம் 30 வரிசைகளும் உள்ளன. அடுத்தடுத்த ஒவ்வொரு வரிசையிலும் அதற்கு முந்தைய வரிசையைவிட இரண்டு இருக்கைகள் கூடுதலாக உள்ளன. கடைசி வரிசையில் எத்தனை இருக்கைகள் இருக்கும்?
தீர்வு:
தரவு : a = 20, n = 30, d = 2
tn = a+(n-1)d
t30 = 20+(30-1)2
= 20+29×2
= 20+58
= 78
எனவே கடைசி வரிசையில் உள்ள இருக்கைகளின் எண்ணிக்கை = 78.
கேள்வி 11.
ஒரு கூட்டுத் தொடர்வரிசையில் அமைந்த அடுத்தடுத்த மூன்று உறுப்புகளின் கூடுதல் எனில், அந்த மூன்று உறுப்புகளைக் காண்க.
தீர்வு:
ஒரு கூட்டுத் தொடர் வரிசையில் அடுத்தடுத்த மூன்று உறுப்புகள் a-d, a, a+d என்க.
உறுப்புகளின் கூடுதல் = 27
a – d + a + a + d = 27
3a = 27
a = 27/3
a = 9
பெருக்கற்பலன் = 288
(a-d) x a x (a+d) = 288
(a2-d2) x a = 288
(92-d2)x9 =
81-d2 = 288/9
81-d2 = 32
-d2 = 32-81
-d2 = -49
d2 = 49
d = 7
∴ அடுத்தடுத்த மூன்று உறுப்புகள் = 2, 9, 16
![]()
கேள்வி 12.
ஒரு கூட்டுத் தொடர்வரிசையின் 6-வது மற்றும் 8வது உறுப்புகளின் விகிதம் 7:9 எனில், 9-வது மற்றும் 13- வது உறுப்புகளின் விகிதம் காண்க.
தீர்வு:
தரவு t6:t8 = 7 : 9
a+(6-1)d a+(8-1)d = 7:9
(a+5d) : (a+7d) = 7:9
\(\frac{a+5 d}{a+7 d}=\frac{7}{9}\)
9(a+5d) = 7(a+7d)
9a+45d = 7a+49d
9a-7a = 49d-45d
2a = 4d
a = 2d —–(1)
எனவே t9 :t13 = 9+(9-1)d : a+(13-1)d
= a+8d : a+12d
= 2d+8d : 2d+12d
= 10d : 14d|
= 5:7
ஆகையால் t9 :t13 = 5:7
கேள்வி 13.
ஒரு குளிர்காலத்தில் திங்கள்கிழமை முதல் வெள்ளிக்கிழமை வரை ஊட்டியின் வெப்பநிலை கூட்டுத் தொடர்வரிசையில் உள்ளன. திங்கள் கிழமை முதல் புதன்கிழமை வரை உள்ள வெப்பநிலைகளின் கூடுதல் 0°C மற்றும் புதன்கிழமை முதல் வெள்ளிக்கிழமை வரை உள்ள வெப்பநிலைகளின் கூடுதல் 18°C எனில், ஐந்து நாட்களின் வெப்பநிலைகளைக் காண்க.
தீர்வு:
திங்கள் கிழமை முதல் வெள்ளிக்கிழமை வரை ஊட்டியின் வெப்பநிலை a, b,c,d,e என்க. தரவு: a, b, c,d, e என்பது ஒரு கூட்டுத்தொடர் வரிசை.
a+b+c = ) ——(1)
c+d+e = 18 —–(2)
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம் எனில் b-a = c-b = d-c=e-d b-a = c-b எனில்
2b = c+a ——(3)
c-b = d – c எனில்
2c = b + d ——(4)
If d – c = e – d எனில்
2d = c + e ——(5)
a + b + c = 0 எனில்
2b + b = 0
3b = 0
b = 0
c + d + e = 18 எனில்
2d + d = 18 ((5)லிருந்து)
3d = 18
d = 18/3
d = 6
(4) லிருந்து 2c = 0 + 6 எனில்
c= 6/2
c = 3
a + b + c = 0 எனில்
a + 0 + 3 = ()
c + d + e = 18 எனில்
3 + 6 + e = 18 (எனில் (5))
9 + e = 18
e = 18 – 9
e = 9
5 நாட்களின் வெப்பநிலைகள் = -3°C, 0°C, 3°C,6°C 9°C.
![]()
கேள்வி 14.
பிரியா தனது முதல் மாத வருமானமாக ₹15,000 ஈட்டுகிறார். அதன் பிறகு ஒவ்வோர் ஆண்டும் அவரது மாத வருமானம் ₹1500 உயர்கிறது. அவளுடைய முதல் மாத செலவு ₹13,000 மற்றும் அவளது மாதாந்திரச் செலவு ஒவ்வோர் ஆண்டும் ₹900 உயர்கிறது. பிரியாவின் மாதாந்திரச் சேமிப்பு ₹20,000 அடைய எவ்வளவு காலம் ஆகும்.
தீர்வு:
a = 15000-13000 = 2000
d = 1500-900 = 600
tn = 20000
tn = a+(n-1)d
2000+(n-1)(600) = 20000
(n-1)(600) = 20000-2000 600n-600 = 18000
600n = 18000+600
600n = 18600
n = \(\frac{18600}{600}\)
n = 31
பிரியாவின் மாதாந்திர சேமிப்பு = ₹20,000 ஐ அடைய ஆகும் காலம் 31 வருடங்கள் ஆகும்.